332. 重新安排行程

没有视频题解，先行跳过
重点在于容器的选择和回溯参数的确定

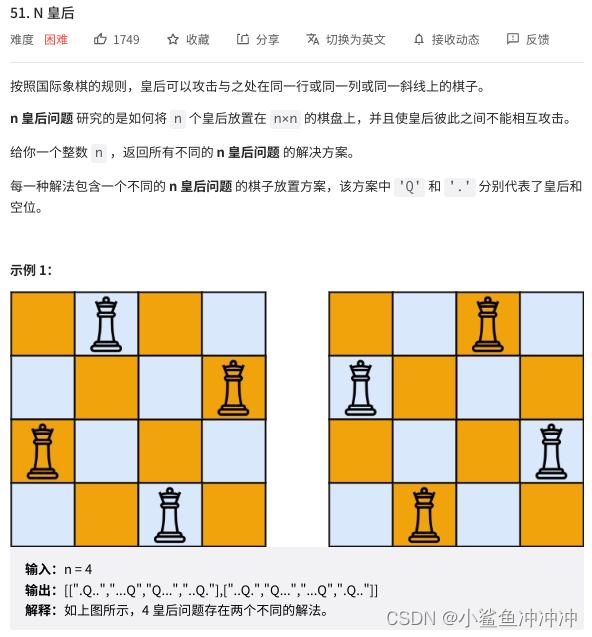
51. N 皇后

教程视频：https://www.bilibili.com/video/BV1Rd4y1c7Bq/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891

解法一：回溯

这里可以将棋盘的每一行看作一次递归，即棋盘行数确定了树的深度。
同时，每一行中可供选择的位置为树层中的遍历的内容，即for循环每次遍历单行中所有列，棋盘的列数决定了树的宽度。

class Solution {
    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        //初始化一个空棋盘
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }

    //n是棋盘大小，row控制递归深度（树的深度），chessboard等效于回溯中的path
    public void backTrack(int n, int row, char[][] chessboard) {
        //遍历到叶子节点，收集结果
        if(row==n){
            res.add(Array2List(chessboard));
            return;
        }
        //col控制for循环上限（树的宽度）
        for (int col = 0;col < n; col++) {
            //判断当前位置(row,col)是否可以放置棋子
            if (isValid (row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backTrack(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }

    //功能函数，检查当前位置(row,col)是否可以放置棋子
    //（因为chessboard从上往下放置棋子，仅判断当前行上方即可）
    public boolean isValid(int row, int col, int n, char[][] chessboard) {
        // 检查col列是否可以放置
        for (int i=0; i<row; ++i) { // 相当于剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }

        // 检查135度对角线是否可以放置
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // 检查45度对角线是否可以放置
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }

    //功能函数，将二维数组char[][]转为LIst<String>
    public List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();

        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }
}

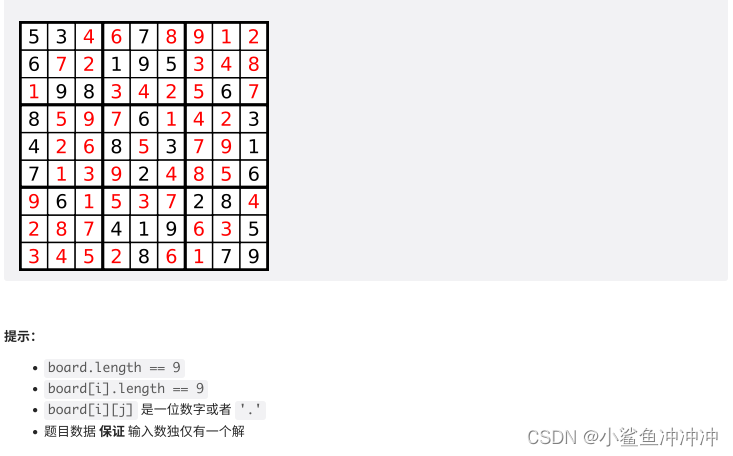
37. 解数独

教程视频：https://www.bilibili.com/video/BV1TW4y1471V/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891

解法一：

需要填满整个数独，因此数独棋盘空格个数决定了递归深度（数的深度）。本题的难点就是递归位置要用嵌套for循环寻找。
每一个空格有‘1’-‘9’九个选项，因此树的每一层的宽度为9。
当找到一个可能的结果立即结束回溯，因此回溯函数右返回值。

class Solution {
    public void solveSudoku(char[][] board) {
        solveSudokuHelper(board);
    }

    private boolean solveSudokuHelper(char[][] board){
        // 一个for循环遍历棋盘的行，一个for循环遍历棋盘的列
        for (int i = 0; i < 9; i++){ // 遍历行
            for (int j = 0; j < 9; j++){ // 遍历列
                if (board[i][j] != '.'){ // 跳过原始数字
                    continue;
                }
                // 当前位置为(i,j)，遍历这个位置放9个数字的可能性。
                for (char k = '1'; k <= '9'; k++){ 
                    // 判断(i, j) 这个位置放k是否合适
                    if (isValidSudoku(i, j, k, board)){
                        board[i][j] = k;
                        if (solveSudokuHelper(board)){ // 如果找到合适一组立刻返回
                            return true;
                        }
                        board[i][j] = '.';
                    }
                }
                // 9个数都试完了，都不行，那么说明解决不了数独问题，返回false（本题一定有解，因此程序不会走到这里）
                 //「这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！」
                return false;
            }
        }
        // 遍历完所有位置，都没有返回false，说明当前爱你棋盘被正确地填满了，返回true
        return true;
    }


    //判断棋盘(row,col)位置填写val是否合法
    private boolean isValidSudoku(int row, int col, char val, char[][] board){
        // 同行是否重复
        for (int i = 0; i < 9; i++){
            if (board[row][i] == val){
                return false;
            }
        }
        // 同列是否重复
        for (int j = 0; j < 9; j++){
            if (board[j][col] == val){
                return false;
            }
        }
        // 9宫格里是否重复
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++){
            for (int j = startCol; j < startCol + 3; j++){
                if (board[i][j] == val){
                    return false;
                }
            }
        }
        return true;
    }
}

总结

本节都是难度较高的回溯题，只要准确分辨控制树的深度和宽度的因素即可正确解题。