图神经网络的数学基本原理

@作者DeepHub IMBA，个人学习记录

图神经网络

单个图神经网络(GNN)层有一堆步骤，在图中的每个节点上会执行:
- 消息传递
- 聚合
- 更新
这些组成了对图形进行学习的构建块，GDL的创新都是在这3个步骤的进行的改变。

节点

节点表示一个实体或对象，如用户或原子。因此节点具有所表示实体的一系列属性。这些节点属性形成了节点的特征(即“节点特征”或“节点嵌入”)。

通常，这些特征可以用Rd中的向量表示． 这个向量要么是潜维嵌入，要么是以每个条目都是实体的不同属性的方式构造的。

这些节点特征是GNN的输入，每个节点i具有关联的节点特征xi∈Rd和标签yi(可以是连续的，也可以是离散的，就像单独编码一样)。

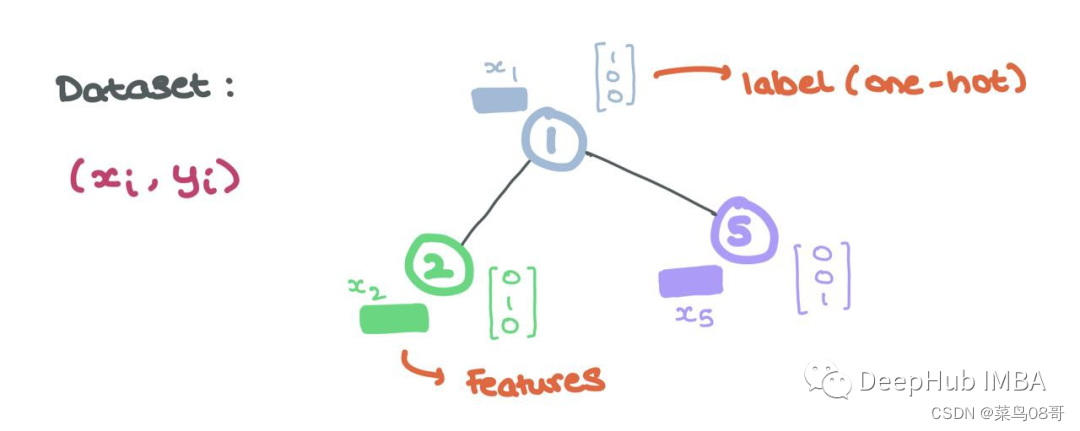
边

边也可以有特征aij∈Rd '例如，在边缘有意义的情况下(如原子之间的化学键)。

消息传递

gnn以其学习结构信息的能力而闻名。通常，具有相似特征或属性的节点相互连接(比如在社交媒体中)。GNN利用学习特定节点如何以及为什么相互连接，GNN会查看节点的邻域。

GNN可以通过查看其邻居Ni中的节点i来了解很多关于节点i的信息。为了在源节点i和它的邻居节点j之间实现这种信息共享，gnn进行消息传递。

对于GNN层，消息传递被定义为获取邻居的节点特征，转换它们并将它们“传递”给源节点的过程。对于图中的所有节点，并行地重复这个过程。这样，在这一步结束时，所有的邻域都将被检查。

让我们放大节点6并检查邻域N6={1,3,4}。我们取每个节点特征x1、x3和x4，用函数F对它们进行变换，函数F可以是一个简单的神经网络(MLP或RNN)，也可以是仿射变换F(xj)=Wj⋅xj+b。简单地说，“消息”是来自源节点的转换后的节点特征。
F 可以是简单的仿射变换或神经网络。现在我们设F(xj)=Wj⋅xj为了方便计算 ⋅ 表示简单的矩阵乘法。

聚合

现在我们有了转换后的消息{F(x1)，F(x3)，F(x4)}传递给节点6，下面就必须以某种方式聚合(“组合”)它们。
有很多方法可以将它们结合起来。常用的聚合函数包括:

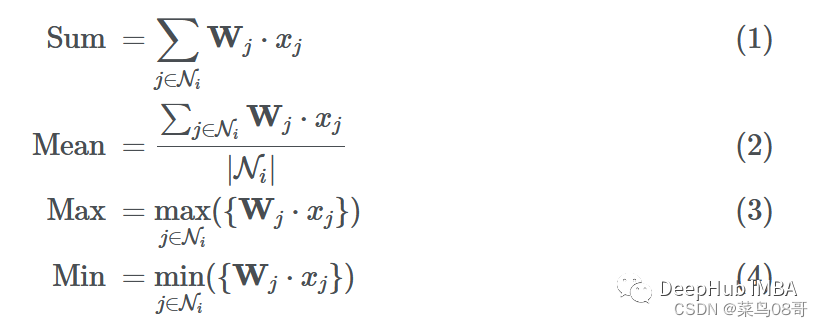
假设我们使用函数G来聚合邻居的消息(使用sum、mean、max或min)。最终聚合的消息可以表示为:

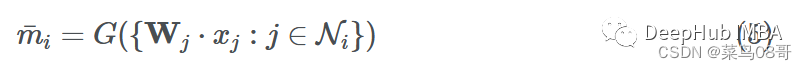
更新

使用这些聚合消息，GNN层就要更新源节点i的特性。在这个更新步骤的最后，节点不仅应该知道自己，还应该知道它的邻居。这是通过获取节点i的特征向量并将其与聚合的消息相结合来操作的，一个简单的加法或连接操作就可以解决这个问题。

• 使用加法
  
  其中σ是一个激活函数(ReLU, ELU, Tanh)， H是一个简单的神经网络(MLP)或仿射变换，K是另一个MLP，将加法的向量投影到另一个维度。

• 使用连接
  
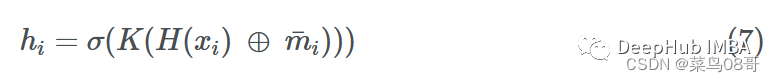
  为了进一步抽象这个更新步骤，我们可以将K看作某个投影函数，它将消息和源节点嵌入一起转换:
  
  初始节点特征称为xi，在经过第一GNN层后，我们将节点特征变为hi。假设我们有更多的GNN层，我们可以用hli表示节点特征，其中l是当前GNN层索引。同样，显然h0i=xi(即GNN的输入)。

整合在一起

现在我们已经完成了消息传递、聚合和更新步骤，让我们把它们放在一起，在单个节点i上形成单个GNN层：

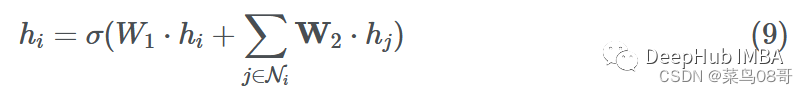
这里我们使用求和聚合和一个简单的前馈层作为函数F和H。设hi∈Rd, W1,W2⊆Rd ’ ×d其中d '为嵌入维数。

使用邻接矩阵

到目前为止，我们通过单个节点i的视角观察了整个GNN正向传递，当给定整个邻接矩阵a和X⊆RN×d中所有N=∥V∥节点特征时，知道如何实现GNN正向传递也很重要。
在 MLP 前向传递中，我们想要对特征向量 xi 中的项目进行加权。这可以看作是节点特征向量 xi∈Rd 和参数矩阵 W⊆Rd′×d 的点积，其中 d′ 是嵌入维度：
如果我们想对数据集中的所有样本(矢量化)这样做，我们只需将参数矩阵和特征矩阵相乘，就可以得到转换后的节点特征(消息):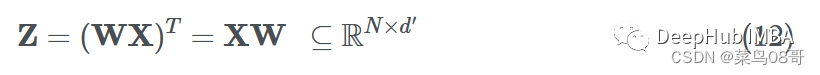

在gnn中，对于每个节点i，消息聚合操作包括获取相邻节点特征向量，转换它们，并将它们相加(在和聚合的情况下)。

单行Ai对于Aij=1的每个指标j，我们知道节点i和j是相连的→eij∈E。例如，如果A2=[1,0,1,1,0]，我们知道节点2与节点1、3和4连接。因此，当我们将A2与Z=XW相乘时，我们只考虑列1、3和4，而忽略列2和5：


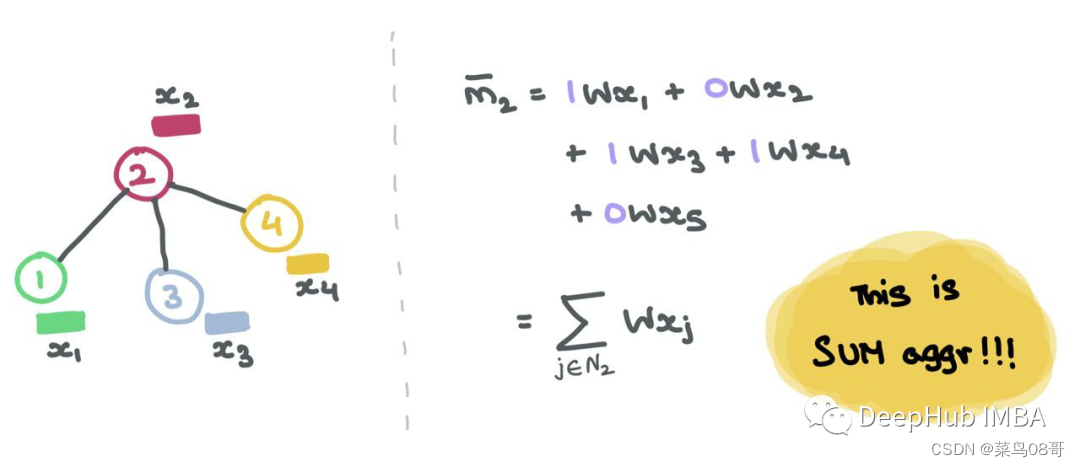
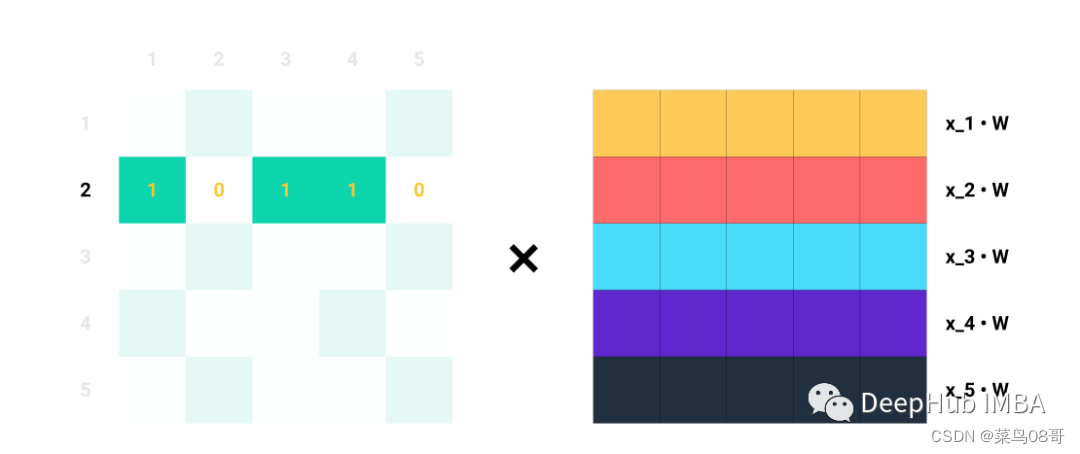
矩阵乘法就是A中的每一行与Z中的每一列的点积，这就是消息聚合的含义!!

获取所有N的聚合消息，根据图中节点之间的连接，将整个邻接矩阵A与转换后的节点特征进行矩阵乘法:

但是这里有一个小问题:观察到聚合的消息没有考虑节点i自己的特征向量(正如我们上面所做的那样)。所以我们将自循环添加到A(每个节点i连接到自身)。

这意味着对角线的而数值需要进行修改，用一些线性代数，我们可以用单位矩阵来做这个!


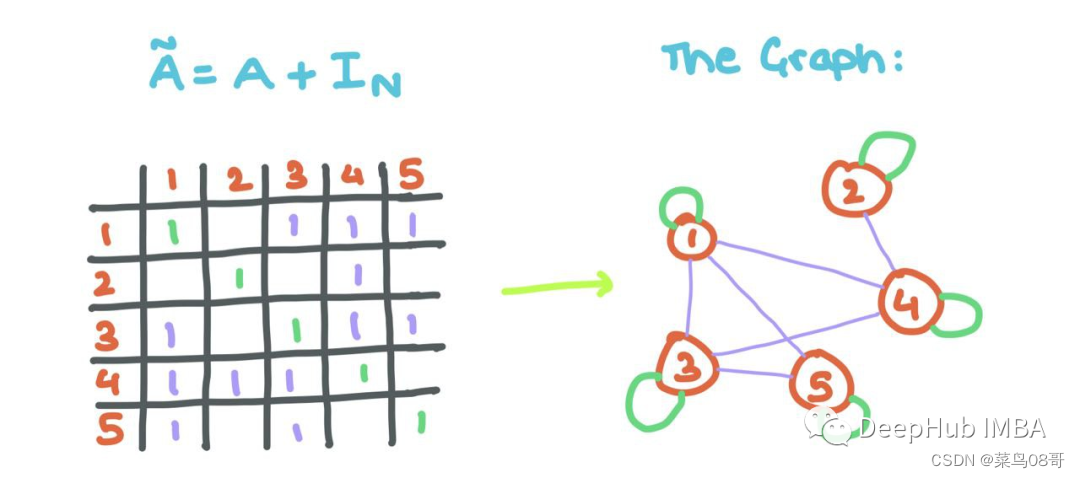
添加自循环可以允许GNN将源节点的特征与其邻居节点的特征一起聚合！！！有了这些，你就可以用矩阵而不是单节点来实现GNN的传递。
⭐要执行平均值聚合（mean），我们可以简单地将总和除以1，对于上面的例子，由于A2=[1,0,0,1,1]中有三个1，我们可以将∑j∈N2Wxj除以3，但是用gnn的邻接矩阵公式来实现最大（max）和最小聚合（min）是不可能的。

GNN层堆叠

上面我们已经介绍了单个GNN层是如何工作的，那么我们如何使用这些层构建整个“网络”呢?信息如何在层之间流动，GNN如何细化节点(和/或边)的嵌入/表示?

每个h1→N∈HL都可以被堆叠，并被视为一批样本。我们可以很容易地将其视为批处理。

对于给定的节点i, GNN聚合的第l层具有节点i的l跳邻域。节点看到它的近邻，并深入到网络中，它与邻居的邻居交互。

这就是为什么对于非常小、稀疏(很少边)的图，大量的GNN层通常会导致性能下降：因为节点嵌入都收敛到一个向量，因为每个节点都看到了许多跳之外的节点。对于小的图，这是没有任何作用的。

这也解释了为什么大多数GNN论文在实验中经常使用≤4层来防止网络出现问题。

以节点分类为例训练GNN
在训练期间，对节点、边或整个图的预测可以使用损失函数(例如:交叉熵)与来自数据集的ground-truth标签进行比较。也就是说gnn能够使用反向传播和梯度下降以端到端方式进行训练。

训练和测试数据

1、Transductive

训练数据和测试数据都在同一个图中。每个集合中的节点相互连接。只是在训练期间，测试节点的标签是隐藏的，而训练节点的标签是可见的。但所有节点的特征对于GNN都是可见的。

我们可以对所有节点进行二进制掩码(如果一个训练节点i连接到一个测试节点j，只需在邻接矩阵中设置Aij=0)。

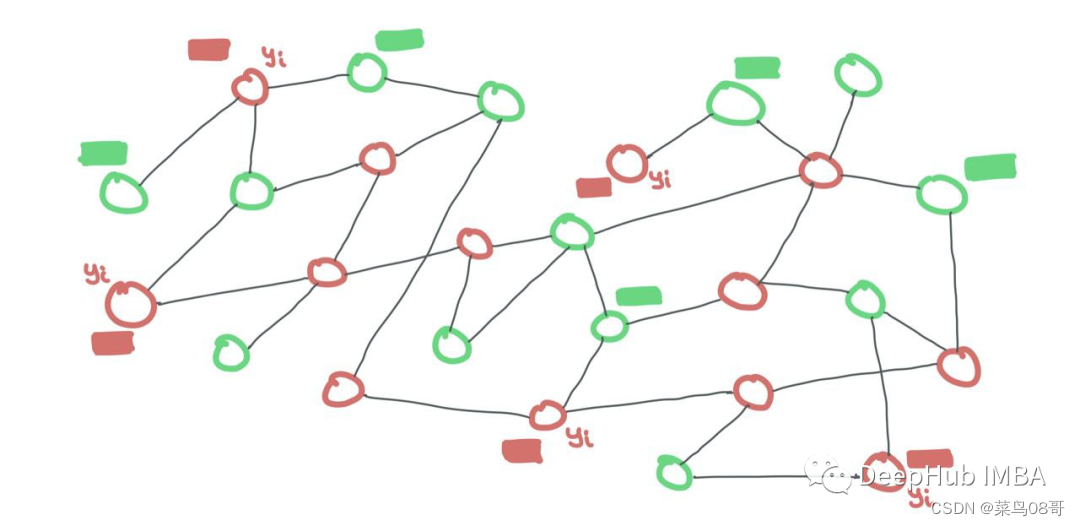
训练节点和测试节点都是同一个图的一部分。训练节点暴露它们的特征和标签，而测试节点只暴露它们的特征。测试标签对模型隐藏。二进制掩码需要告诉GNN什么是训练节点，什么是测试节点。

2、Inductive

另外一种方法是单独的训练图和测试图。这类似于常规的ML，其中模型在训练期间只看到特征和标签，并且只看到用于测试的特征。训练和测试在两个独立的图上进行。这些测试图分布在外，可以检查训练期间的泛化质量。

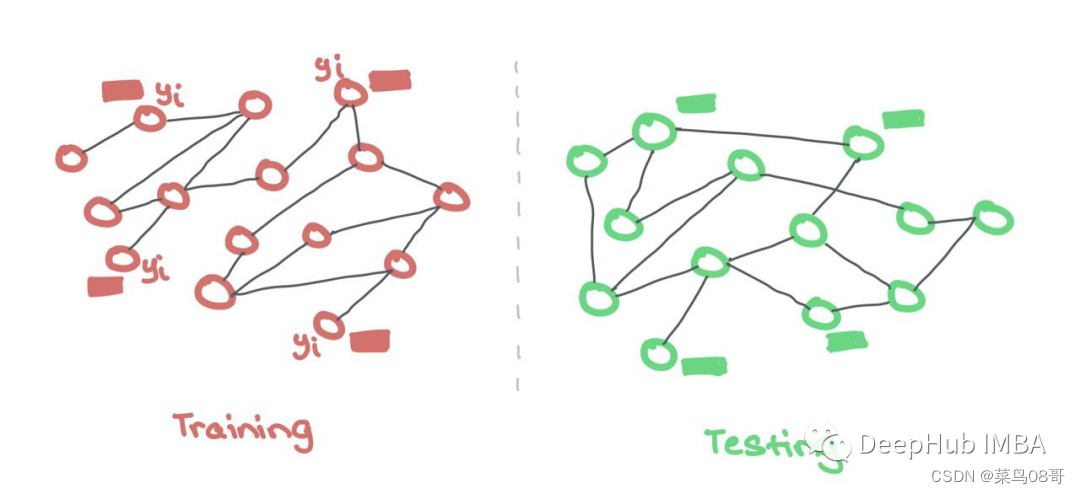
与常规ML一样，训练数据和测试数据是分开保存的。GNN只使用来自训练节点的特征和标签。这里不需要二进制掩码来隐藏测试节点，因为它们来自不同的集合。

反向传播和梯度下降

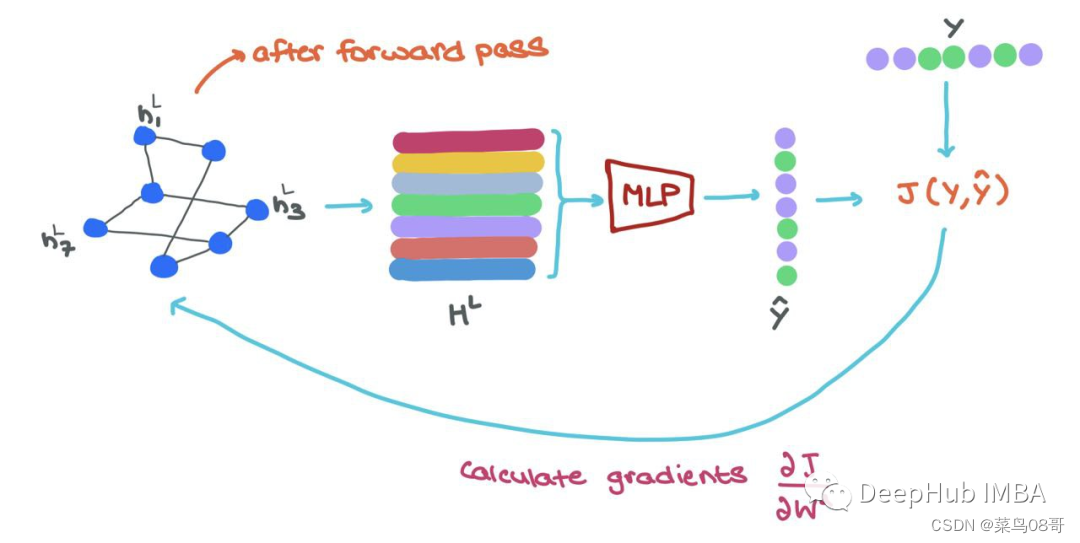
在训练过程中，一旦我们向前通过GNN，我们就得到了最终的节点表示hLi∈HL， 为了以端到端方式训练，可以做以下工作:

• 将每个hLi输入MLP分类器，得到预测^yi
• 使用ground-truth yi和预测yi→J(yi,yi)计算损失
• 使用反向传播来计算∂J/∂Wl，其中Wl是来自l层的参数矩阵
• 使用优化器更新GNN中每一层的参数Wl
• (如果需要)还可以微调分类器(MLP)网络的权重。