《剑指 Offer》专项突破版 - 面试题 30 和 31:详解如何设计哈希表以及利用哈希表设计更加高级、复杂的数据结构
目录
一、哈希表的基础知识
二、哈希表的设计
2.1 - 插入、删除和随机访问都是 O(1) 的容器
2.2 - 最近最少使用缓存
一、哈希表的基础知识
哈希表是一种常见的数据结构,在解决算法面试题的时候经常需要用到哈希表。哈希表最大的优点是高效,在哈希表中插入、删除或查找一个元素都只需要 O(1) 的时间。因此,哈希表经常被用来优化时间效率。
在 C++ 中,哈希表有两个对应的类型,即 unordered_set 和 unordered_map。如果每个元素都只有一个值,则用 unordered_set。例如,unordered_set 在图搜索时经常用来存储已经搜索过的节点。如果每个元素都存在一个值到另一个值的映射,那么就用 unordered_map。例如,如果要存储一个文档中的所有单词,同时还关心每个单词在文档中出现的位置,则可以考虑用 unordered_map,单词作为 unordered_map 的键而单词的位置作为值。
尽管哈希表是很高效的数据结构,但这并不意味着哈希表能解决所有的问题。如果用哈希表作为字典存储若干单词,那么只能输入完整的单词在字典中查找。如果对数据集中的元素排序能够有助于解决问题,那么用 set 或 map(第 8 章)可能更合适。如果需要知道一个动态数据集中的最大值或最小值,那么堆(第 9 章)的效率可能更好。如果希望能够根据前缀进行单词查找,如查找字典中所有以 "ex" 开头的单词,那么应该用前缀树(第 10 章)作为实现字典的数据结构。
二、哈希表的设计
与链表、数组等基础数据结构相比,哈希表相对而言要复杂得多。如何设计一个哈希表,是很多面试官非常喜欢的面试题。下面简要地介绍设计一个哈希表的要点。
设计哈希表的前提是待存入的元素需要一个能计算自己哈希值的函数。哈希表根据每个元素的哈希值把它存储到合适的位置。
template<class K>
struct DefaultHashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct DefaultHashFunc<std::string>
{
size_t operator()(const std::string& str)
{
// BKDRHash
size_t hash = 0;
size_t seed = 131;
for (char ch : str)
{
hash = hash * seed + ch;
}
return hash;
}
};哈希表最重要的特点就是高效,只需要 O(1) 的时间就可以把一个元素存入或读取。在常用的基础数据结构中,数组满足这个要求。只要知道数组中的下标,就可以用 O(1) 的时间存入或读取一个元素。因此,可以考虑基于数组实现哈希表。
把哈希值转换成数组下标可以采用的方法是对数组的长度求余数。如果数组的长度是 4,待存入的元素的哈希值为 5,由于 5 除以 4 的余数是 1,那么它将存入数组下标为 1 的位置。同理,如果待存入的元素的哈希值为 2 和 3,那么它们分别存入下标为 2 和 3 的位置。此时哈希表的状态如下图 (a) 所示。
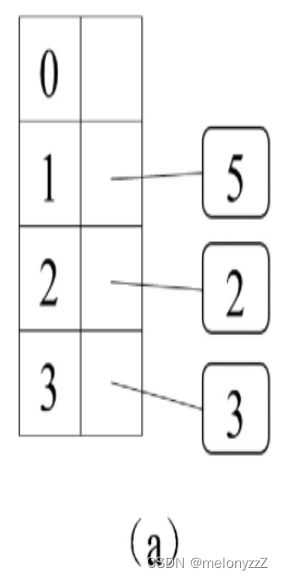
再在哈希表中存入一个哈希值为 7 的元素。由于 7 除以 4 的余数为 3,因此它存入的位置应该是 3。下标为 3 的位置之前已经被哈希值为 3 的元素占用。如果将两个哈希值不同的元素存入数组中的同一个位置,会引发冲突。
为了解决这种冲突,可以把存入数组中同一个位置的多个元素用链表存储。也就是说,数组中每个位置对应的不是一个元素,而是一个链表。哈希值为 3 和 7 的两个元素都存放在数组下标为 3 的位置,因此它们实际上存入了同一个链表中。接下来如果再添加哈希值分别为 4 和 8 的两个元素,那么它们都将被存入数组下标为 0 的位置对应的链表中。此时哈希表的状态如下图 (b) 所示。不难想象,如果在哈希表中添加更多的元素,那么就会有更多的冲突,有更多的元素被存入同一个链表中。
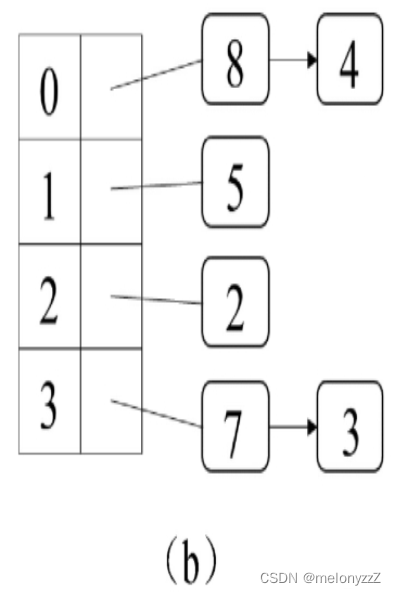
接着考虑如何判断哈希表中是否包含一个元素。例如,为了判断哈希表中是否包含哈希值为 7 的元素,由于 7 除以 4 的余数是 3,因此先找到数组下标为 3 的位置对应的链表,然后从头到尾扫描这个链表查看是否有哈希值为 7 的元素。
在链表中做顺序扫描的时间复杂度为 O(n),链表越长查找需要的时间就越长。这就违背了设计哈希表最重要的一个初衷:存入和读取一个元素的时间复杂度为 O(1)。因此,必须确保链表不能太长。
可以计算哈希表中元素的数目与数组长度的比值。显然,在数组长度一定的情况下,存入的元素越多,这个比值就越大;在存入元素的数目一定的情况下,数组的长度越长,这个比值就越小。
当哈希表中元素的数目与数组长度的比值超过某一阈值时,就对数组进行扩容(通常让数组的长度翻倍),然后把哈希表中的每个元素根据新的数组大小求余并存入合适的位置。例如,在下图 (c) 中,扩容之后数组的长度为 8,这个时候原本存入同一链表的 3 和 7 被分别存入下标为 3 和 7 的位置。
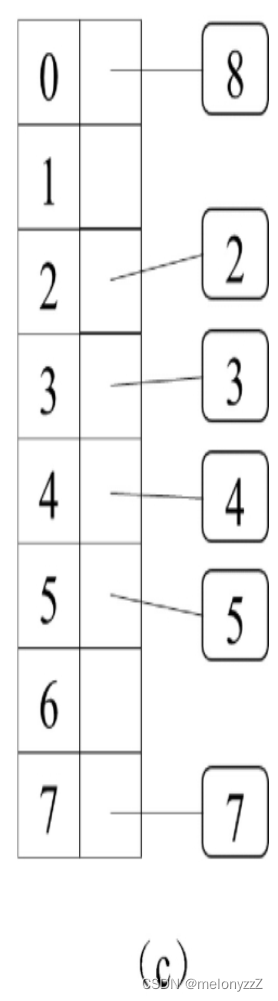
通过对数组进行扩容,原本存入同一链表的不同元素就可能会被分散到不同的位置,从而减少链表的长度。当再在哈希表中添加新的元素时,元素的数目与数组长度的比较可能会再次超过阈值,于是需要再次对数组进行扩容。只要阈值设置得合理,哈希表中的链表就不会太长,仍然可以认为存入和读取的时间复杂度都是 O(1)。
由此可知,设计哈希表有以下 3 个要点:
-
为了快速确定一个元素在哈希表中的位置,可以使用一个数组,元素的位置为它的哈希值除以数组长度的余数。
-
由于多个哈希值不同的元素可能会被存入同一位置,数组的每个位置都对应一个链表,因此存入同一个位置的多个元素都被添加到同一链表中。
-
为了确保链表不会太长,就需要计算哈希表中元素的数目与数组长度的比值。当这个比值超过某个阈值时,就对数组进行扩容并把哈希表中的所有元素重新分配位置。
template<class T>
struct HashNode
{
T _data;
HashNode<T>* _next;
HashNode(const T& data)
: _data(data), _next(nullptr)
{ }
};
template<class K, class T, class KOfT, class HashFunc = DefaultHashFunc<K>>
class HashTable
{
typedef HashNode<T> Node;
private:
/*---------- 数组的长度最好是素数 ----------*/
static size_t GetNextPrime(size_t prime)
{
const int PRIMECOUNT = 28;
static const size_t primeList[PRIMECOUNT] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
size_t i = 0;
for (; i < PRIMECOUNT; ++i)
{
if (primeList[i] > prime)
return primeList[i];
}
return primeList[i];
}
public:
/*---------- 构造函数和析构函数 ----------*/
HashTable()
: _table(GetNextPrime(0), nullptr), _size(0)
{ }
~HashTable()
{
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
/*---------- 查找 ----------*/
bool find(const K& key)
{
HashFunc = hf;
size_t hashAddr = hf(key) % _table.size();
Node* cur = _table[hashAddr];
KOfT kot;
while (cur)
{
if (kot(cur->data) == key)
return true;
cur = cur->_next;
}
return false;
}
/*---------- 插入 ----------*/
bool insert(const T& data)
{
KOfT kot;
if (find(kot(data)) == true)
return false;
HashFunc hf;
size_t hashAddr = hf(kot(data)) % _table.size();
// 头插
Node* newNode = new Node(data);
newNode->_next = _table[hashAddr];
_table[hashAddr] = newNode;
++_size;
// 将装载因子限制在 1 以下
if (_size == _table.size())
{
size_t newSize = GetNextPrime(_table.size());
std::vector<Node*> newTable(newSize, nullptr);
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
// 将 *cur 头插到新表中
size_t hashAddr = hf(kot(cur->data)) % newSize;
cur->_next = newTable[hashAddr];
newTable[hashAddr] = cur;
// 更新 cur
cur = next;
}
_table[i] = nullptr;
}
_table.swap(newTable);
}
return true;
}
/*---------- 删除 ----------*/
bool erase(const K& key)
{
HashFunc hf;
size_t hashAddr = hf(key) % _table.size();
Node* prev = nullptr;
Node* cur = _table[hashAddr];
KOfT kot;
while (cur)
{
if (kot(cur->_data) == key)
{
if (prev == nullptr) // 头删
_table[hashAddr] = cur->_next;
else
prev->_next = cur->_next;
delete cur;
--_size;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
private:
std::vector<Node*> _table; // 哈希表
size_t _size; // 哈希表中存入的元素个数
};除了设计哈希表本身,利用哈希表设计更加高级、更加复杂的数据结构也是一种常见的面试题。下面是几道这种类型的经典面试题。
2.1 - 插入、删除和随机访问都是 O(1) 的容器
题目:
设计一个数据结构,使如下 3 个操作的时间复杂度都是 O(1)。
-
insert(value):如果数据集中不包含一个数值,则把它添加到数据集中。
-
remove(value):如果数据集中包含一个数值,则把它删除。
-
getRandom():随机返回数据集中的一个数值,要求数据集中每个数值被返回的概率都相同。
分析:
由于题目要求插入和删除(包括数据集中是否包含一个数值)的时间复杂度都是 O(1),能够同时满足这些时间效率要求的只有哈希表,因此这个数据结构要用到哈希表。
但是如果只用哈希表,则不能等概率地返回其中的每个数值。如果数值是保存在数组中的,那么很容易实现等概率返回数组中的每个数值。假设数组的长度是 n,那么等概率随机生成 0 到 n - 1 的一个数字。如果生成的随机数是 i,则返回数组中下标为 i 的数值。因此可以发现,需要结合哈希表和数组的特性来设计这个数据容器。
由于数值保存在数组中,因此需要知道每个数值在数组中的位置,否则在删除的时候就必须顺序扫描整个数组才能找到待删除的数值,那么就需要 O(n) 的时间。通常把每个数值在数组中的位置信息保存到一个 unordered_map 中,unordered_map 的键是数值,而对应的值为它在数组中的位置。
下面是这种思路的参考代码。在数据容器 RandomizedSet 中,数值保存在用 vector 实现的动态数组 nums 中,而用 unordered_map 实现的哈希表 numToIndex 中存储了每个数值及其在数组 nums 中的下标。
代码实现:
class RandomizedSet {
public:
bool insert(int val) {
if (numToIndex.count(val) == 1)
return false;
nums.push_back(val);
numToIndex[val] = nums.size() - 1;
return true;
}
bool remove(int val) {
if (numToIndex.count(val) == 0)
return false;
// 避免在数组中删除数组的时候移动数据
int removeIndex = numToIndex[val];
int lastVal = nums[nums.size() - 1];
nums[removeIndex] = lastVal;
nums.pop_back();
numToIndex[lastVal] = removeIndex;
numToIndex.erase(val);
return true;
}
int getRandom() {
int i = rand() % nums.size();
return nums[i];
}
private:
vector<int> nums;
unordered_map<int, int> numToIndex;
};
2.2 - 最近最少使用缓存
题目:
请设计实现一个最近最少使用(Least Recently Used, LRU)缓存,要求如下两个操作的时间复杂度都是 O(1)。
-
get(key):如果缓存中存在键 key,则返回它对应的值;否则返回 -1。
-
put(key, value):如果缓存中之前包含键 key,则它的值设为 value;否则添加键 key 及对应的值 value。在添加一个键时,如果缓存容量已经满了,则在添加新键之前删除最少使用的键(缓存中最长时间没有被使用过的元素)。
分析:
使用哈希表可以让 get 操作和 put 操作的时间复杂度都是 O(1),但普通的哈希表无法找出最近最少使用的键,因此,需要在哈希表的基础上进行改进。
由于需要知道缓存中最近最少使用的元素,因此可以把存入的元素按访问的先后顺序存入链表中。每次访问一个元素(无论是通过 get 操作还是通过 put 操作),该元素都被移到链表的尾部。这样,位于链表头部的元素就是最近最少使用的。
下面考虑如何实现把一个节点移到链表的尾部。这实际上包含两个步骤,首先要把节点从原来的位置删除,然后把它添加到链表的尾部。需要注意的是,在链表中删除一个节点,实际上是把它的前一个节点的 next 指针指向它的下一个节点。如果这个链表是单向链表,那么找到一个节点的前一个节点需要从链表的头节点开始顺序扫描每个节点,也就需要 O(n) 的时间。
为了快速找到一个节点的前一个节点从而实现用 O(1) 的时间删除一个节点,可以用双向链表来存储缓存中的元素。在双向链表中查找一个节点的前一个节点只需要顺着 prev 指针向前走一步,时间复杂度是 O(1)。
因此,设计最近最少使用缓存需要结合哈希表和双向链表的特点。哈希表的键就是缓存的键,哈希表的值为指向双向链表中的节点的指针,每个节点都是一组键与值的数对。
例如,在一个容量为 4(即最多只能插入 4 个键)的最近最少使用缓存中依次插入 (1, 1)、(2, 2)、(3, 3) 和 (4, 4) 这 4 个键与值的数对之后,先后在双向链表中插入 4 个节点,如下图 (a) 所示。此时最近最少使用的键是 1,它的节点位于链表的头部。
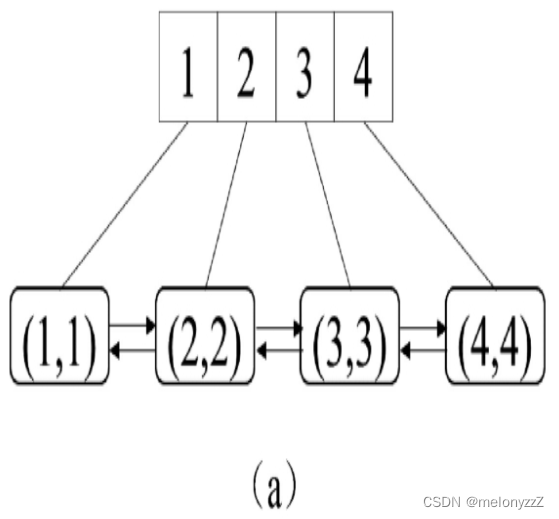
先执行 get(2)。该操作访问键 2,因此它在双向链表中的节点被移到链表的尾部,如下图 (b) 所示。此时最近最少使用的键仍然是 1。

然后执行 put(1, 8),即更新键 1 对应的值。这个操作访问键 1,因此它在链表中的节点被移到了链表的尾部,如下图 (c) 所示。此时最近最少使用的键是 3。
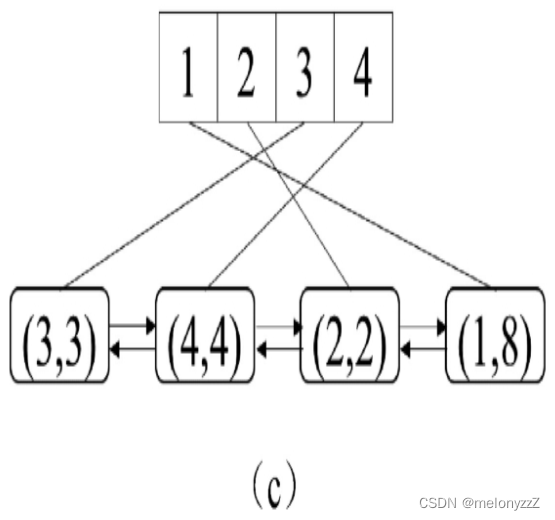
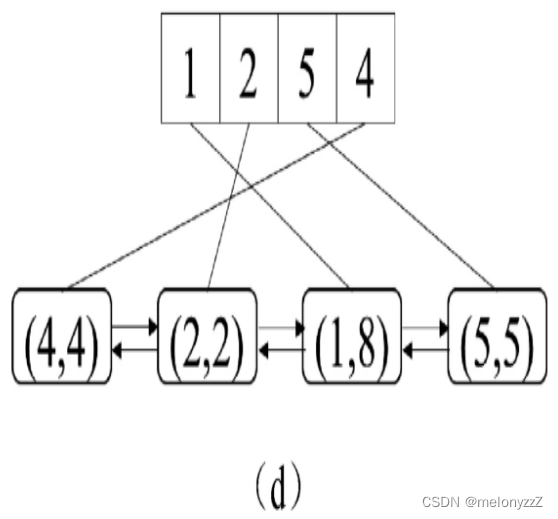
最后执行 put(5, 5),插入一个新的键 5。由于此时缓存已满,在插入新的键之前要把最近最少使用的键 3 及其对应的值删除。位于链表的最前面的节点的键是 3,将键 3 及其对应的值从哈希表和双向链表中删除之后,再把键 5 添加到哈希表中,同时在链表的尾部插入一个新的节点,如下图 (d) 所示。
代码实现:
// 双向链表中的节点的定义
struct Node {
int k;
int v;
Node* prev;
Node* next;
Node(int key = 0, int value = 0)
: k(key), v(value), prev(nullptr), next(nullptr)
{ }
};
class LRUCache {
public:
LRUCache(int capacity)
: cap(capacity)
{
head = new Node;
tail = new Node;
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (mp.count(key) == 0)
return -1;
Node* node = mp[key];
moveToTail(node);
return node->v;
}
void put(int key, int value) {
if (mp.count(key) == 1)
{
Node* node = mp[key];
node->v = value;
moveToTail(node);
return;
}
if (mp.size() == cap)
{
Node* node = head->next;
removeNode(head->next);
mp.erase(node->k);
}
Node* newNode = new Node(key, value);
addToTail(newNode);
mp[key] = newNode;
}
private:
void moveToTail(Node* node) {
removeNode(node);
addToTail(node);
}
void removeNode(Node* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void addToTail(Node* node) {
tail->prev->next = node;
node->prev = tail->prev;
tail->prev = node;
node->next = tail;
}
private:
unordered_map<int, Node*> mp;
// 为了便于在双向链表中添加和删除节点,增加两个哨兵位节点 head 和 tail
Node* head;
Node* tail;
int cap;
};