算法——二分查找算法
1. 二分算法是什么?
简单来说,"二分"指的是将查找的区间一分为二,通过比较目标值与中间元素的大小关系,确定目标值可能在哪一半区间内,从而缩小查找范围。这个过程不断重复,每次都将当前区间二分,直到找到目标值或确定目标值不存在为止。这种分而治之的策略使得二分查找算法具有较高的效率,时间复杂度为O(log n)。
大致图解如下

即通过二段性,在每次判断过后可以一次性减少将近一半的数据,然后通过不断的挪移左右区间来筛选出最后的结果。
2. 朴素二分
在这里我们通过一个例题来讲解:704. 二分查找 - 力扣(LeetCode)
题目描述如下

看到这个题目之后我们首先想到的一定是暴力解法:
从头遍历数组,将每个值与target比较,若遍历到结束还没有找到就返回-1, 否则返回对应下标
我们稍加分析可以发现这个解法的时间复杂度是O(N),我们没有使用到数组升序的性质,我们可以在暴力解法上稍作优化,修改为二分查找:
定义左右指针left, right,然后计算中间值,将其与target比较,由于升序,若中间值小于target,则表明此时中间值及其左边的值均小于target,此时target理应存在于[mid+1, right],因此令left = mid+1; 若中间值大于target,则表明此时中间值及其右边的值均小于target, 此时target理应存在于[left, mid-1],因此令right = mid-1;相等时返回mid下标即可。
大致图解如下

代码如下
class Solution
{
public:
int search(vector<int>& nums, int target)
{
int left = 0, right = nums.size() - 1;
while (left <= right)
{
// int mid = (left + right) / 2;
int mid = left + (right - left) / 2; // ֹ避免整型溢出
if (nums[mid] < target) left = mid + 1;
else if (nums[mid] > target) right = mid - 1;
else return mid;
}
return -1;
}
};在这里有两个值得关注的细节,其中一个是while循环的结束条件,在这里由于left与right的变化始终是在mid的基础上+1或-1,因此在left==right的时候,会因为边界的变化而导致退出循环,因此退出的条件是left > right;另一个是mid的计算方式,在计算mid时我们有两种计算方式:一种是mid = left + (right - left) / 2,另一种是mid = left + (right - left + 1) / 2,这两种方式在具体的过程中体现为

可以看到两种计算方式只有在数据个数为偶数时才会发生变化,意为分别取到中左与中右的下标。
朴素二分的模板
模板如下
while (left <= right)
{
int mid = left + (right - left) / 2;
if (......)
left = mid + 1;
else if (......)
right = mid - 1;
else
return ......;
}3. 查找左边界二分
讲解 查找左边界二分与查找右边界二分 时,我们使用例题:34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
题目描述如下

简单分析后我们可以得出一个简单的暴力解法:
从头到尾遍历一遍数组,使用begin与end分别标识一下这个元素第一次出现与最后一次出现的位置并返回,否则返回{-1, -1}
我们可以在此基础上优化:
定义左右指针left, right与标识符begin, end,寻找元素的第一次出现位置本质就是查找左边界,而寻找元素的最后一次出现位置本质就是查找右边界。
在查找左边界时,计算出中间值并将其与target比较,如果中间值<target,说明左边界理应存在于[mid+1, right]区间中,因此left = mid+1,如果中间值>=target,说明左边界理应存在于[left, mid]区间中,因此right = mid;
查找左边界图解如下

在查找左边界时,我们同样需要关注两个细节:
1. while 循环的退出条件:在上面的查找过程中我们可以发现查找到最后left与right可能会指向同一个位置,此时如果使用while (left <= right)则会陷入死循环,因此退出条件为left>=right
2. 中点下标的选取方式:在朴素二分那里我们知道选取方式有两种,在这里我们选取左边中点,其图解如下

可以看到,如果选取右边的中点可能会导致死循环或下标进入不合理区间
因此我们可以得到查找左边界代码如下
// 查找左端点
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid;
}
if (nums[left] == target) begin = left; // 确认是否找到左边界,并标记左边界查找左边界二分的模板
模版如下
while (left < right)
{
int mid = left + (right - left) / 2;
if (......) left = mid + 1;
else right = mid;
}4. 查找右边界二分
在查找右边界时,计算出中间值并将其与target比较,如果中间值>target,说明右边界理应存在于[left, mid-1]区间中,因此right = mid-1,如果中间值<=target,说明右边界理应存在于[mid, right]区间中,因此left = mid;
查找右边界图解如下

与查找左边界类似,我们同样需要关注两个细节
1. while 循环的退出条件:同上,在查找过程中我们可以发现查找到最后left与right可能会指向同一个位置,此时如果使用while (left <= right)则会陷入死循环,因此退出条件为left>=right
2. 中点下标的选取方式:在朴素二分那里我们知道选取方式有两种,在这里我们选取右边中点,其图解如下

可以看到,如果选取左边的中点可能会导致死循环或下标进入不合理区间
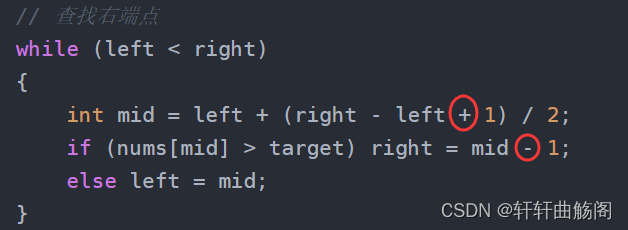
因此我们可以得到查找右边界代码如下
left = 0, right = nums.size() - 1;// 重置下标
// 查找右端点
while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target) right = mid - 1;
else left = mid;
}
if (nums[right] == target) end = right;// 标识位查找右边界二分的模板
模板如下
while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (......) right = mid - 1;
else left = mid;
}解决问题完整代码如下
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
// 边界处理
if (nums.size() == 0) return { -1, -1 };
int begin = -1, end = -1;
int left = 0, right = nums.size() - 1;
// 查找左端点
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid;
}
if (nums[left] == target) begin = left;
left = 0, right = nums.size() - 1;
// 查找右端点
while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target) right = mid - 1;
else left = mid;
}
if (nums[right] == target) end = right;
return { begin, end };
}
};5. 小结
二分查找算法的细节比较多,但是当我们真正把它分析透彻后,我们仅需要结合理解背住模板,即
对于分类讨论的代码,我们具体情景具体实现
对于中点的选取,我们为了快捷可以记:分类讨论出现 -1 的时候上面就 +1
即