张维迎《博弈与社会》讨价还价与耐心(1)讨价还价问题
讨价还价问题
合作与冲突
讨价还价(bargaining)在现实生活中普遍存在。例如,签订劳资合同时,雇员和雇主会就工作时间、工作条件、工资待遇、合同期限等方面进行讨价还价行为。合伙人之间会就资金的投入、股权的占比、利润的分配进行讨价还价。企业破产或重组时,利益相关者要就债务清偿、职工安置等问题讨价还价。生活中,夫妇之间谁来照看孩子,谁来做家务,可能也要讨价还价。离婚时涉及财产分配、子女抚养等问题,讨价还价更为复杂。在政治领域,政治家要就人事安排、权力划分讨价还价。中央和地方之间需要就税源的分配、转移支付的多少、配套资金的划拨等做出安排。国际上,中美之间的贸易摩擦、中日有关钓鱼岛的争议、朝鲜半岛核问题的六方会谈,等等,都是讨价还价的过程,达不成协议,可能爆发战争。
讨价还价问题的特点在于参与其中的当事方既有共同利益,又有利益冲突。即一般来说,只要达成协议,对于当事各方都有好处;但是,讨价还价可以达成不同的协议,产生不同的利益分配,使得各方得到的好处各异。这使得讨价还价问题非常类似前面第三章提到的多重均衡问题。即在一个博弈中,均衡太多了,反而有可能阻止任何一个均衡的出现。讨价还价达不成协议的原因,往往是因为可以达成的协议太多了:每一方都希望达成对于自己有利的协议,结果反倒可能任何协议都无法达成了。
但讨价还价中的多重均衡问题也不同于前面讲的可以用某种标准来加以衡量的多重均衡。例如,根据帕累托标准,如果一个博弈中存在两个纳什均衡,其中一个均衡帕累托优于另外一个均衡,则博弈的所有参与人会选择第一个均衡。又例如前面提到的交通规则问题,为避免冲突,所有的人会都选择靠左行走,或者都选择靠右行走。在这些例子中,参与者之间没有太大的利益分歧。而在讨价还价问题中,参与人之间存在利益冲突。但这种利益冲突也不同于零和博弈中的利益冲突,在零和博弈中一方得到的是另一方所失去的。讨价还价如果达不成协议,则所有人都会有损失。如果达成协议,各方都得到好处,各方收益之和大于零。从这个意义来讲,讨价还价问题实质上是一种具有利益冲突的正和博弈。
合作博弈与非合作博弈
研究讨价还价问题一般有两种思路。
一种是合作博弈方法(cooperative game approach),另一种为非合作博弈方法(non-cooperative game approach)。合作博弈研究的视角是假定参与讨价还价的各方联合做决策,强调的是集体理性,协议追求的是集体利益的最大化,各方会自愿地遵守形成的决策或达成的协议。而非合作博弈研究的出发点是假定参与讨价还价的每一方都独立做出决策,强调的是个体理性,各方追求的是个人利益的最大化。这意味着,即使达成了一个能够给各方带来集体利益最大化的协议,如果这个协议不是一个纳什均衡,也不会得到执行。例如前面讲的囚徒困境的例子,两个囚徒可以达成“都抵赖”的协议,就是抓起来之后谁都不坦白,但是真正被逮捕之后,他们从各自利益最大化角度决策,就会都选择坦白了。需要注意的是,合作博弈理论和非合作博弈理论的区别,不是前者研究合作,后者研究不合作,而是做出决策的过程是基于个人理性还是集体理性。如我们将在以后的章节中看到的,非合作博弈理论是我们研究如何达成合作的最适当的理论。
下面我们先从合作博弈的角度来讨论讨价还价问题,然后再从非合作博弈的角度研究讨价还价。
谈判砝码与谈判能力
蛋糕的大小与分配
合作博弈中一个非常重要的概念是纳什谈判解(Nash bargaining solution)。这个概念是诺贝尔经济学奖得主约翰·纳什在1950年发表的《讨价还价问题》(the bargaining problem)一文中提出的。下面,我们用一个简单的卖画例子来解释这一概念。
设想有一个画家准备卖掉自己创作的一幅画。他可以自己直接到市场上去卖,也可以交给画廊去卖。如果他自己去卖的话,这幅画可以卖1000块钱;如果交给画廊卖的话,这幅画可以卖到3000块钱。对于画廊来说,如果不接受该画家的委托,而是去卖其他作品,画廊的收入是500元。这样,如果画家委托画廊卖画,总收益为3000元;如果画家自己卖画,画廊卖其他的作品,总体收益为1500元。显然,从总体收益来看,画家与画廊合作卖画是有效的。现在的问题是:画家如果委托画廊把画卖了出去之后,双方如何分配这3000块钱?画家和画廊应各拿多少?
现在把这个问题一般化。假如现在有两个参与者:一个A,代表画家;一个B,代表画廊。他们两个人分配数额为V的财富。如果他们能够达成协议的话,就按照协议分配;如果达不成协议的话,第一个人得到a,第二个人得到b。对应上面卖画的例子,V=3000, a=1000, b=500。这里a、b的数值被称作“威胁点”(threat point),即如果谈判破裂了,每一方可以得到的利益。这时回复到非合作状态,因此威胁点也叫做“谈判砝码”(bargaining power)。画家的砝码a=1000,画廊的砝码b=500。需要注意的是,在一般情况下,a+b一定要小于V,如果它们之和大于V,就不可能存在帕累托改进,谈判也就没有意义了。正因为a+b<V,才有帕累托改进,合作才有价值。这也表明,V-a-b必须是正数,即为合作带来剩余(surplus)。
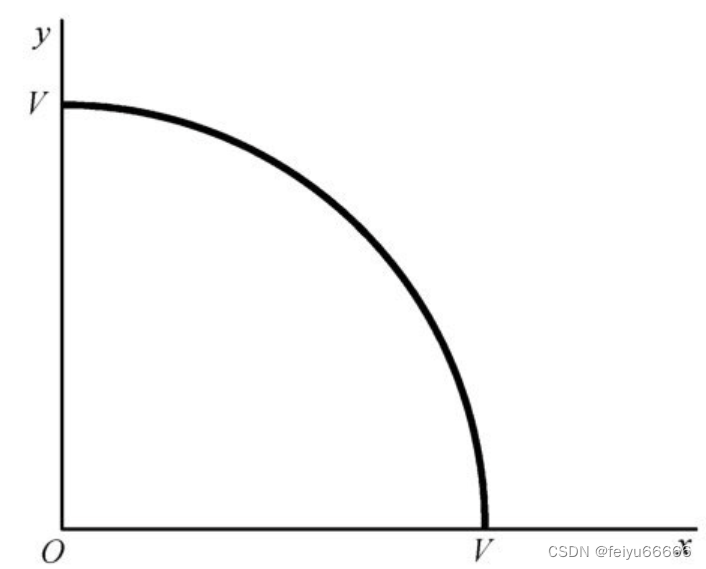
一般地,如果我们用x代表参与者A在谈判中得到的数额,用y代表B得到的数额,应该有x+y=V,即两个人刚好将所有价值分配完。[插图]如果我们用h和k分别代表两个人在总剩余价值中得到的份额,那么h+k=1。根据定义容易得出:x=a+h(V-a-b); y=b+k(V-a-b)。具体如图所示,我们用横坐标代表A得到的数额x,纵坐标代表B得到的数额y,那么总价值V可以全部给A,也可以全部给B。所以V-V这一条连线是可行分配的边界线。所有分配方案均不可能超过这条线。点P代表前面提到的威胁点,其坐标为(1000,500),表明如果谈不成的话,画家自己卖画可以得到1000元,画廊代理其他作品可以得到500元。从图中可以看出,任何一种分配不能处在P点左侧或者下方。因为,如果达成协议的状况比原来还要糟糕,每一个理性的参与者为什么还要签署协议呢?所以满足个人理性的可行的协议合作解一定在阴影围起的三角形区域。
前面讨论的例子中,讨价还价中可分配的总价值V是固定的。但是实际生活中,V值可以是不固定的。例如,如果分配比例不合适,画廊卖的积极性就不高;或者,如果协议是在画创作完成之前签订的话,画家也可能没有积极性把画画得完美,从而导致最终卖不到3000元的价格。所以图5-1中V-V这条线不一定是一条直线,更可能是一条曲线边界,如图5所示。
这种情况在社会分配问题中最为突出。设想一个由两个人组成的社会,社会的生产需要两个人相互合作。假定两个人的能力相当,对社会贡献相等。进行分配时,一人一半的话,就能有最大的利益。而如果一个人得到的多而另外一个人得到的少,少的这个人就没有积极性工作了。此时,另外一个人再有积极性工作也没有用。但是,如果人的能力是不对等的,对社会的贡献也不相同,此时进行平均分配的话,每个人都会没有积极性工作。如果不平均分配的话,反而每个人都有比较大的积极性工作。但是如果太不平均了,又都会不好好工作。这说明分配问题(分蛋糕问题)和生产问题(做蛋糕问题)不能完全分开。在不同的分配方案或制度下,一个社会做出的蛋糕大小会有很大的不同。如果我们假定所有蛋糕都是固定的话,最公平的分配是给每个人同样的份额,也就是平均主义的分配方式。如果蛋糕的大小是不固定的,我们就不能采用平均主义分配,否则会使蛋糕变小。这就是我们在讨论制定分配政策的时候应该着重考虑的问题。
纳什谈判解
下面来分析纳什谈判解(Nash bargaining solution)。纳什谈判解建立在以下三个公理化条件之上:(1)帕累托有效(Pareto efficiency);(2)线性转换不变性(invariance of linear transformation);(3)对非相关选择的独立性(independence of irrelevant alternatives)。
条件(1)是讨价还价的效率标准,表明最后达成的协议应该是帕累托最优的。从图形上来看,意味着分配方案应该是在可分配财富的边界线上,而不能在这条线里边,如果在这条线里边就不是帕累托最优的。因为如果某个解在边界线里面,那么至少有一个人可以在不损害他人利益的情况下得到更多,故这个解不是一个帕累托最优解。因此,条件(1)意味着我们的分配方案一定要分配掉所有的剩余,就像我们前面分3000元钱,一定要把这些钱分完,不能剩下。
条件(2)的含义是对效用函数进行线性转化不影响讨价还价的结果,类似将摄氏温度转化成华氏温度并不改变温度本身一样。这是经济学中预期效用理论的基本假设,每一个人的期望效用水平不受度量的标量的影响。有了这一假设后,我们还可以把多维谈判问题约减为一维谈判问题。一维谈判指的是谈判双方仅就一个方面展开谈判。比如,卖画问题中双方仅就价格展开谈判。但实际上,现实中的谈判往往是多维的:双方不仅要就价格展开谈判,还会就付款方式、交易期限、是否可以退货等展开谈判。每一个维度的得失都会对当事人的效用带来一定影响,我们把不同维度带来的效用加总后,就可以近似地看成一个维度的谈判问题了,从而可以使讨价还价模型简单化。
条件(3)无关选择的独立性,简单地说,就是如果原来可行的选择没有被选择,那么去掉这些无关的选择,不会影响讨价还价的结果。例如,在前面卖画的例子中,画家得1200、画廊得1800是可行的,如果协议不包含这一选择,那么即使在约束中去掉这一选择,协议也不会改变。这就是无关选择独立性的含义。
纳什证明:如果所有参与者都认可上述这三个公理性假设,而且知道对方也都认可这三个假设,即这些假设成为“共同知识”(common knowledge),那么,双方讨价还价就等价于在满足可行分配约束x+y≤V(x,y)的前提下最大化如下(两人的)社会福利目标函数:
W(x,y)=
,这个社会福利函数可以理解为每个人净收益(或效用)对数的加权平衡,其中的权数是各自在剩余价值中的份额。求解该最优化问题,可以得出下面的等式:
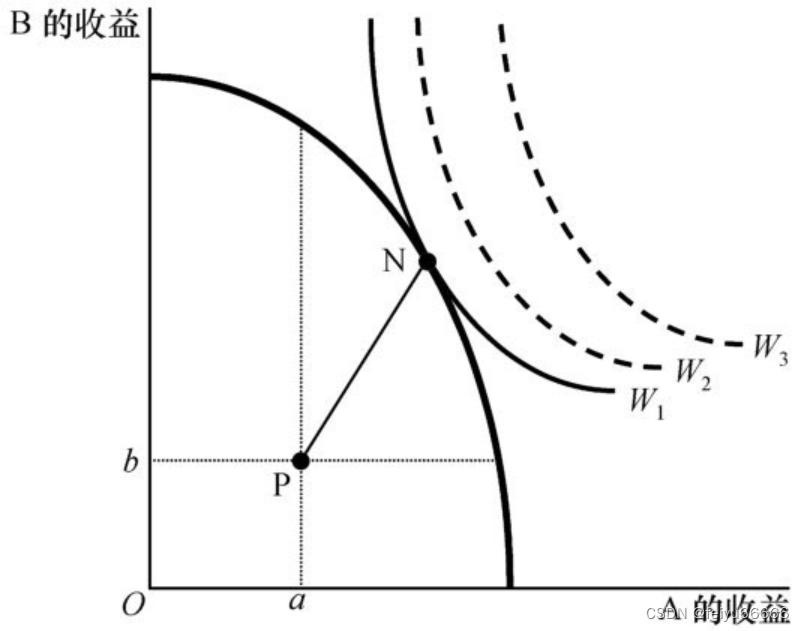
,这实际上是剩余在双方之间的分配比例。如图所示,它表示连接N点和P点连线的斜率。
上图中,N点代表的是无差异曲线W1和可行分配线的切点,是福利最大化的点。如果在这个点之内,代表的福利水平就变小了;如果在这个点之外,尽管福利水平更高,但超出可分配的总财富,是不可行的。P点是双方的威胁点,或者说是保留价格点,表示如果双方无法达成协议,一方得到a,另一方得到b。