堆排序-Python实现

简述

堆排序（Heap Sort）是一种基于比较的排序算法，它利用堆这种数据结构所设计的一种排序算法。堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

堆

堆排序中的堆有大顶堆、小顶堆两种。他们都是完全二叉树。

完全二叉树是指除了最后一层外，每一层都是完全填充的，并且最后一层的右边都是空的二叉树。大顶堆和小顶堆都是特殊的完全二叉树，它们的特点分别是每个节点的值都不小于（或不小于）其子节点的值，和每个节点的值都不大于（或不小于）其子节点的值。

将该堆按照排序放入列表

• 大顶堆：所有的父节点的值都比孩子节点大，叶子节点值最小。root 根节点是第一个节点值最大公式表示：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
• 小顶堆：和大顶堆相反，所有父节点值，都小于子节点值，root 根节点是 第一个节点值最小公式表示：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

ok，了解了这些定义。接下来，我们来看看堆排序的基本思想及基本步骤。

堆排序基本思想及步骤

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

在堆的结构中，堆中的最小值（最大值）总是位于堆的根结点。在堆排序中主要分为三步：
（1）创建大顶堆（BuildMaxHeap）：将待排序元素列中的所有元素进行排列，生成一个大顶堆；
（2）将堆顶元素与末尾元素进行交换，将最大元素“沉”到元素列末端；
（3）调整顶堆，使其满足大顶堆定义；
（4）重复（2）（3）步骤，直至元素列有序。

以大顶堆为例

构造大顶堆

• 如何调整
  我们从最后一个非叶子节点处开始调整。最后一个非叶子节点是最后一个叶子节点的父节点。
  若父节点的下标为 i ，那么左孩子节点下标为 i × 2 + 1，右孩子节点下标为 i × 2 + 2。
  设元素列的长度为 N，因为下标从0开始，所以最后一个叶子节点的下标是 N - 1。
  分两种情况：第一种是最后一个叶子节点是左孩子节点，那么 n - 1 = i × 2 + 1，即 i = n / 2 - 1
  第二种情况是最后一个叶子节点是右孩子节点（此时 n 是奇数）那么 n - 1 = i × 2 + 2，即 i = ( n - 1 ) / 2 - 1 = n / 2 - 1（向下取整）
  综上，最后一个非叶子节点的下标是 n / 2 - 1

• 构造大根堆

  以升序排序序列 [20，50，20, 40, 70，10，80, 30，60]为例

  它对应的二叉树结构如下：

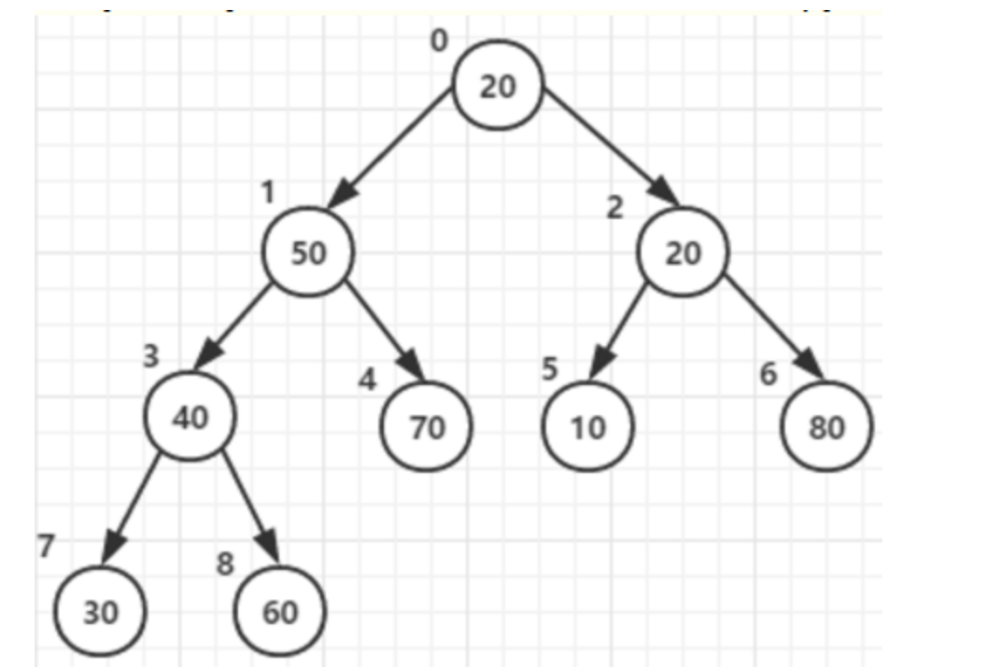
在我们的例子中，最后一个非叶子节点的下标是 9 / 2 - 1 = 3，因此调整顺序为：3–>2 -->1 -->0。

1. 从最后一个父节点开始，将父节点、他所有的子节点中的最大值交换到父节点。父节点：3

2. 将倒数第二个父节点同理交换，父节点：2

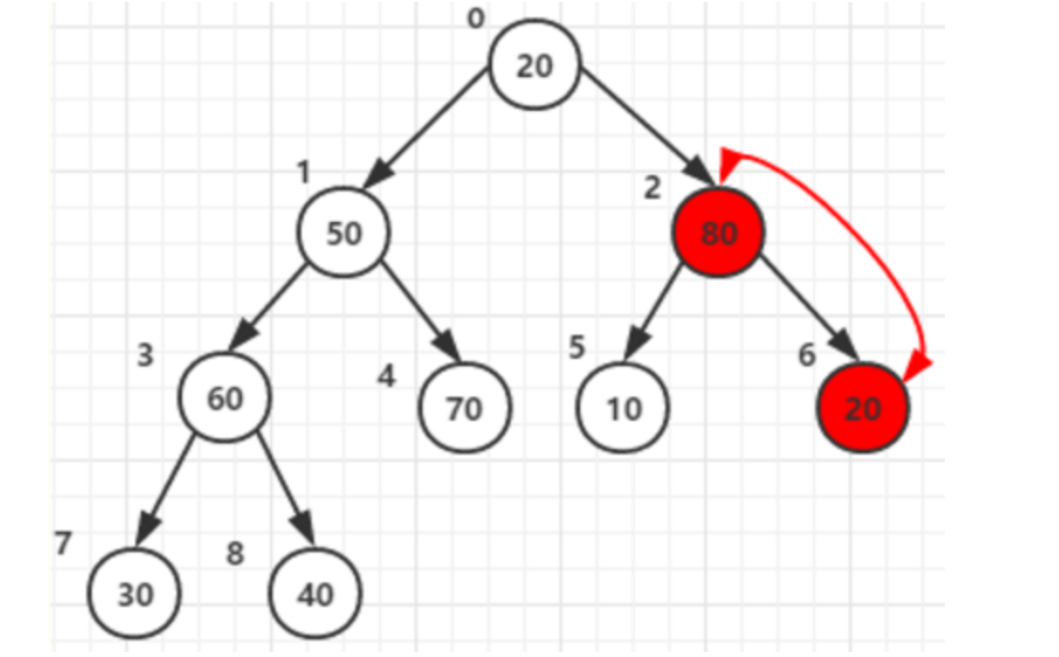
3. 继续调整父节点：1

4. 最后是根节点：0

5. 注意很重要：务必注意-承接第3步。
   假设根节点值为：10， 当他和两个子节点70， 80。
   

父节点和两子节点中的大的(80)交换后位于父节点2：原来80的位置。

可是他还有子节点，且子节点中的值比根节点大，那就还需要以他为父节点构造一次，与子节点6 值为20交换一次。

同理在其他所有父节点的构造中都需要判断调整
忽略第五步。构造好的的大顶堆如下:

堆排序简略版

基本思路：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。可称为有序区，然后将剩余n-1个元素重新构造成一个堆，估且称为堆区(未排序)。这样会得到n个元素的次小值。重复执行，有序区从:1—>n，堆区：n–>0，便能得到一个有序序列了。
每次将堆顶（根节点）最的的元素和堆尾列表最后一个元素交换，80 和40交换
即上面说的堆区(未排序)：n–>0最大元素（根节点），和有序区从:1—>n，最后一个元素交换

按照上面原理继续排序，70， 30 交换。然后调整堆

堆顶元素60尾元素20交换后–>调整堆

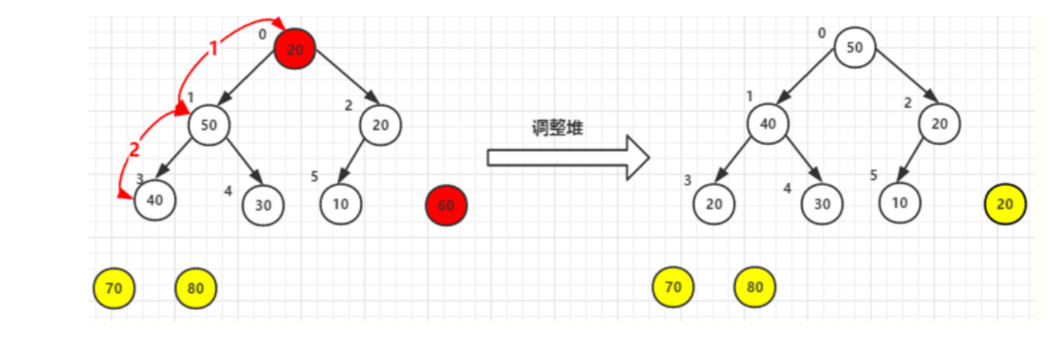
最后结果

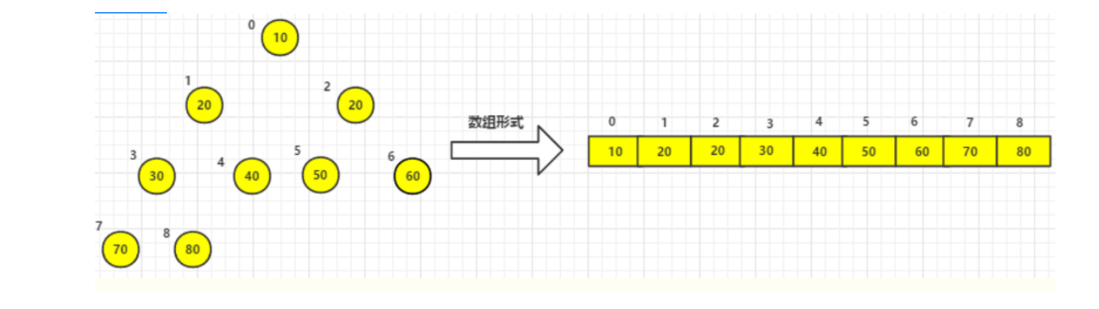
堆排序-python代码实现

现在排序这么一个序列：list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]

    """
    堆排序  heap_sort
    
                         4
                       /   \
                     7      0
                   /  \    / \
                 9    1   5   3
               / \   /
             3   2  6
    
    list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]
    """

代码实现一

    def swap(data, root, last):
        data[root], data[last] = data[last], data[root]
    
    #调整父节点 与孩子大小， 制作大顶堆
    def adjust_heap(data, par_node, high):
    
        new_par_node = par_node
        j = 2*par_node +1   #取根节点的左孩子， 如果只有一个孩子 high就是左孩子，如果有两个孩子 high 就是右孩子
    
        while j <= high: #如果 j = high 说明没有右孩子，high就是左孩子
            if j < high and data[j] < data[j+1]: #如果这儿不判断 j < high 可能超出索引
                # 一个根节点下，如果有两个孩子，将 j  指向值大的那个孩子
                j += 1
            if data[j] > data[new_par_node]: #如果子节点值大于父节点，就互相交换
                data[new_par_node], data[j] = data[j], data[new_par_node]
                new_par_node = j #将当前节点，作为父节点，查找他的子树
                j = j * 2 + 1
    
            else:
                # 因为调整是从上到下，所以下面的所有子树肯定是排序好了的，
                #如果调整的父节点依然比下面最大的子节点大，就直接打断循环，堆已经调整好了的
                break
    
    
    # 索引计算: 0 -->1 --->....
    #    父节点 i   左子节点：2i +1  右子节点：2i +2  注意：当用长度表示最后一个叶子节点时 记得 -1
    #    即 2i + 1 = length - 1 或者 2i + 2 = length - 1
    #    2i+1 + 1 = length 或 2i+2 + 1 = length
    #    2(i+1)=length 或 2(i+1）+1 = length
    #    设j = i+1  则左子节点(偶数)：2j = length 和 右子节点(基数)：2j+1 = length
    #    2j//2 = j == (2j+1)//2 这两个的整除是一样的，所以使用length//2 = j 然后 i + 1 = j
    #    i = j-1  = length//2 -1  #注意左子节点:2i+1 //2 =i  而右子节点：(2i+2)//2 = i+1 
    
    # 从第一个非叶子节点(即最后一个父节点)开始，即 list_.length//2 -1（len(list_)//2 - 1）
    
    # 开始循环到 root 索引为：0 的第一个根节点， 将所有的根-叶子 调整好，成为一个 大顶堆
    def heap_sort(lst):
        """
        根据列表长度，找到最后一个非叶子节点，开始循化到 root 根节点，制作 大顶堆
        :param lst: 将列表传入
        :return:
        """
        length = len(lst)
        last = length -1  #最后一个元素的 索引
        last_par_node = length//2 -1
    
        while last_par_node >= 0:
    
            adjust_heap(lst, last_par_node, length-1)
            last_par_node -= 1  #每调整好一个节点，从后往前移动一个节点
    
        # return lst
    
        while last > 0:
            #swap(lst, 0, last)
            lst[0], lst[last] = lst[last],lst[0]
            # 调整堆让 adjust 处理，最后已经排好序的数，就不处理了
            adjust_heap(lst, 0, last-1)
            last -= 1
    
        return lst #将列表返回
    
    
    
    if __name__ == '__main__':
        list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]
        heap_sort(list_)
        print(list_)
    
    
    #最后结果为：
    [0, 1, 2, 3, 3, 4, 5, 6, 7, 9]

代码实现二

    import math
    
    def heap_sort(a):
        al = len(a)
    
        def heapify(a, i):
            left = 2 * i + 1
            right = 2 * i + 2
            largest = i
            if left < al and a[left] > a[largest]:
                largest = left
            if right < al and a[right] > a[largest]:
                largest = right
    
            if largest != i:
                a[i], a[largest] = a[largest], a[i]
                heapify(a, largest)
    
        # 建堆
        for i in range(math.floor(len(a) / 2), -1, -1):
            heapify(a, i)
    
        # 不断调整堆：根与最后一个元素
        for i in range(len(a) - 1, 0, -1):
            a[0], a[i] = a[i], a[0]
            al -= 1
            heapify(a, 0)
        return a
    
    
    if __name__ == '__main__':
        list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]
        heap_sort(list_)
        print(list_)
    
    
    #最后结果为：
    [0, 1, 2, 3, 3, 4, 5, 6, 7, 9]