深度学习（生成式模型）—— Consistency Models

前言

Diffusion model需要多次推断才能生成最终的图像，这将耗费大量的计算资源。前几篇博客我们已经介绍了加速Diffusion model生成图像速率的DDIM和Stable Diffusion，本节将介绍最近大火的Consistency Models（代表模型：Dalle-3），其允许Diffusion model仅经过一次推断就生成最终的图像，同时也允许少量多次推断来生成最终的图像。

预备知识：SDE与ODE

yang song博士在《Score-Based Generative Modeling Through Stochastic Differential Equations》一文中提出可以使用SDE（随机微分方程）来刻画Diffusion model的前向过程，并且用SDE统一了Score-based Model (NCSN)和DDPM的前向过程与反向过程。此外，SDE对应了多个前向过程，即从一张图到某个噪声点的加噪方式有多种，但其中存在一个ODE（常微分方程）形式的前向过程，即不存在随机变量的确定性的前向过程。

具体可查看前一篇博客score-based generative modeling through stochastic differential equations

Method

Consistency Models的核心可总结为上图，在一条ODE轨迹上（可以简单理解为从一个图像到某个噪声点，每一个步骤加的噪声都是特定的，比如第一步加的噪声为0.1，第二步加的噪声为0.2，一旦图像确定了，则对应的噪声点也会被确定），训练一个模型$f_{\theta }(x_t,t)$，其满足对于任意的$t、t^{\prime }$，模型的输出都一致，即
$$f_{\theta }(x_t,t)=f_{\theta }(x_{t^{\prime }},t^{\prime })\text{\hspace{1em}(1.0)}$$

模型$f_{\theta }(x_t,t)$即为Consistency Models，这里有个关键点，即训练Consistency Models时，必须是在ODE轨迹上。如果是在SDE轨迹，如下图所示，则有一个x对应多个y的情况出现，从同一个点出发，第一次迭代对应的轨迹是黑线，第二次迭代对应的轨迹是红线，模型将很难收敛。

为了实现式1.0，则只需要采样ODE轨迹上的两个点$x_t$，$x_{t^{\prime }}$，在套用一个L2 或L1 loss即可。
我们可以使用一系列的ODE solver（即在反向过程中不会引入随机性噪声的Diffusion model，例如DDIM）来帮助我们确定ODE轨迹上的两个点。

注意到式1.0也是自监督学习的优化目标，因此也会有收敛到奔溃解的情况，比如模型所有参数都为0，因此作者选用了自监督学习中的MoCo解决此类问题。

上述思路总结出的训练策略为Consistency Distillation，一个训练范式如下图

如下图，作者也给出了上述算法一些理论上的性质，个人觉得不是本算法的核心，故不总结

此外，作者也提出了Consistency Training的训练策略，即通过往一张图像里持续添加一个固定的噪声来获得一个ODE轨迹

个人猜测特，当$t_n$取值为0时，则会将$f_{{\theta }^{-}}(x)$替换为$x_0$，即原图，此时模型拟合完毕后，则有

$$f_{\theta }(x_T,T)=f_{\theta }(x_{T-1},T-1)=...=f_{\theta }(x_1,1)=x_0$$

此时我们只需要进行一次采样，即可得到原图。由此可见，Consistency Models其实是在直接预测$x_0$，但是在训练时把预测$x_0$拆分成了多步。

如下图所示，Consistency Models也支持进行多步采样，反向过程的算法长啥样取决于使用的ODE轨迹是什么。

实验结果

CD表示训练策略为Consistency Distillation，CT表示训练策略为Consistency Training，整体表现上CD优于CT，Dalle3也是使用CD训练的。NFE表示反向过程迭代次数

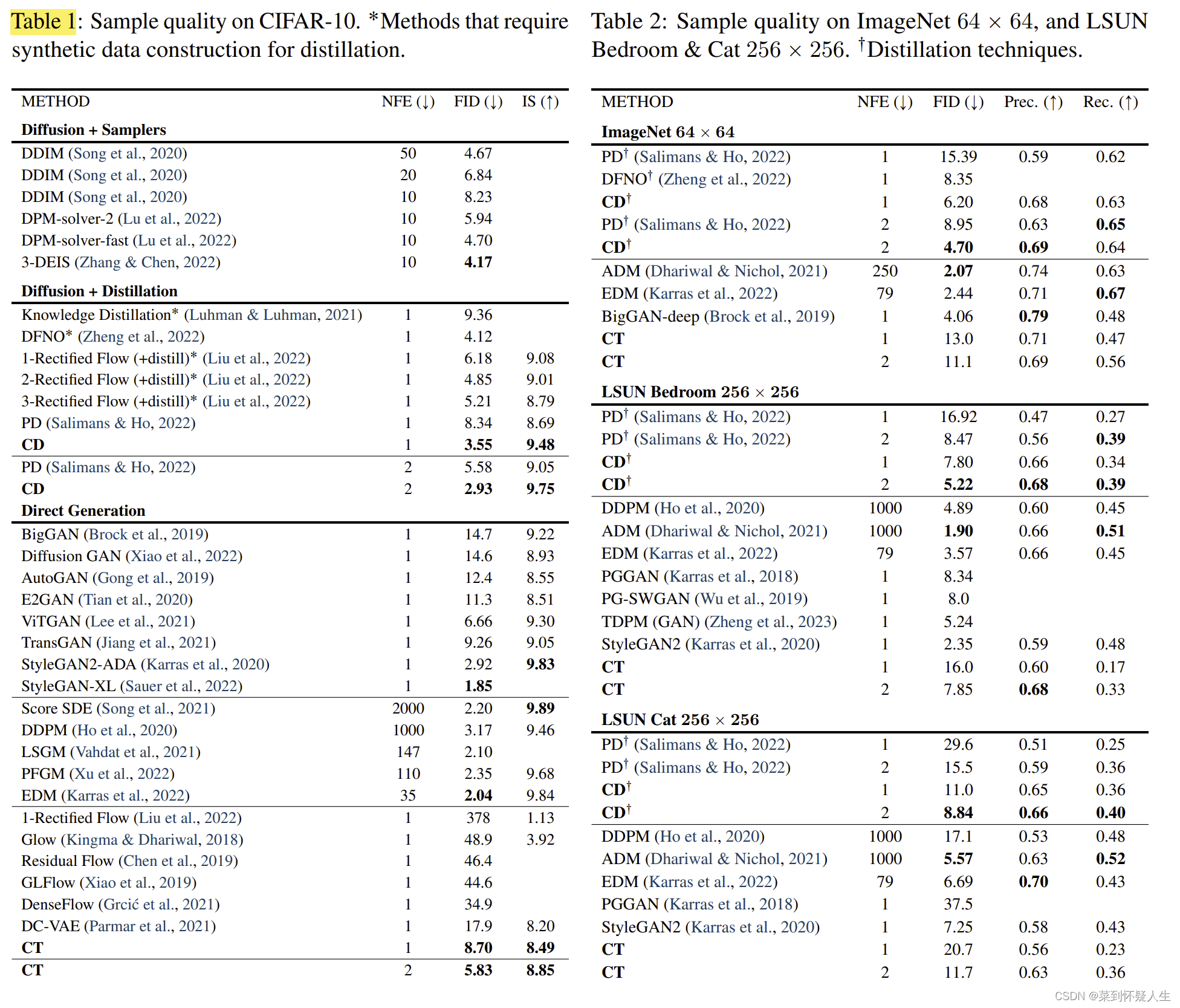
可以看到Consistency Distillation的策略整体优于Consistency Training，看起来采用什么ODE轨迹也会影响到Consistency Models的性能