分布式存储中常见的容错机制:多副本、纠删码(RS、LRC、SHEC)
文章目录
- 分布式存储中常见的容错机制
- 浴缸原理
- 多副本
- 纠删码
- RS
- LRC
- SHEC
- 总结
分布式存储中常见的容错机制
浴缸原理
在存储领域中,通常我们会使用浴缸曲线来描述硬盘的故障率,如下图。
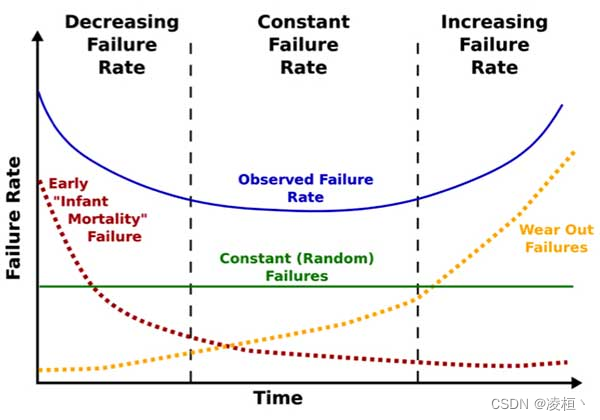
故障率随着时间变化,主要分为三个阶段:
- 早期适配型故障:早期在引入新设备时,会出现系统、软/硬件、驱动等适配型原因的故障。当完成设备适配后,这一类型的故障会急剧下降。
- 中期偶发型故障:中期设备正常运转时,故障率较低且运行稳定,偶尔可能会因为操作失误、次品设备等原因出现小概率故障。
- 末期损耗型故障:在设备长期运转后,硬盘由于老化出现各种各样的问题,例如扇区错误/磁盘坏块(HDD)、闪存磨耗/LFT映射表损坏(SSD)等,此时会大规模出现硬件故障。
在分布式存储中,通常采用增加存储节点来扩充系统的容量,这就导致随着系统中的硬盘设备增加,维护的难度越来越大,故障的风险也随之增加,因此需要通过某种容错策略来确保数据安全。
多副本
在传统的分布式存储中,通常会采用多副本的容错策略,常见的用例如 HDFS 中就采用了三副本的策略 。
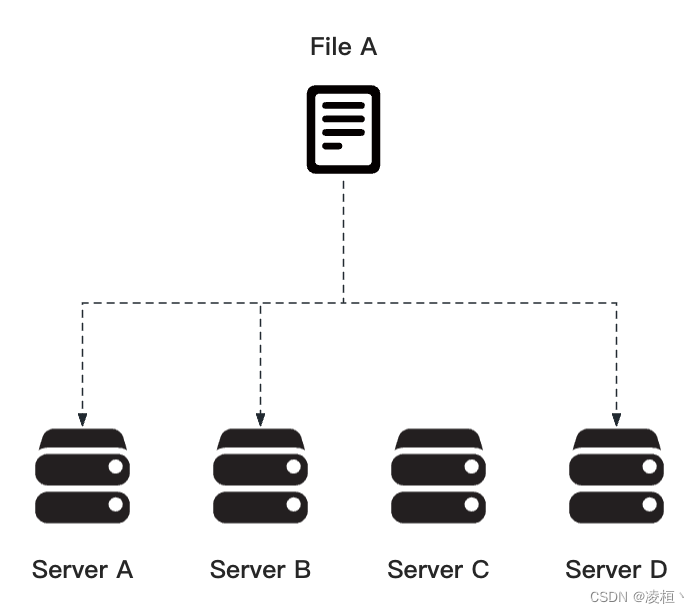
多副本顾名思义,采用了数据冗余的方式,将同样的数据拷贝到存储系统中的 N 个节点上。当某个节点的数据丢失时,只要系统中还有任意一个存活的副本,就可以将数据恢复。
其实现简单,数据恢复速度快,可靠性高(只要有一个副本存活,数据就不会丢失)。但也因此导致了严重的空间浪费,因此通常在存储小文件、热点文件时,才会使用多副本。
纠删码
纠删码(Erasure Code)是一种用于纠正数据丢失的校验编码。如下图,通常我们会讲输入数据拆分为多个数据块,再根据某种算法在数据块的基础上编码出校验块。当出现数据块丢失时,可以通过剩余的数据块和校验块进行解码,将丢失数据恢复回来。
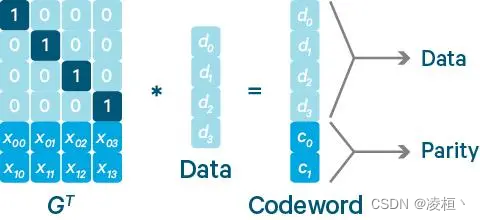
由于编码、解码的计算流程复杂,开销过大,所以通常只有大文件和冷数据才会使用纠错码进行容错。
RS
RS(Reed-Solomon)是当前最为主流的纠删码算法,例如 Google GFS、Facebook HDFS、Dell EMC ECS、CEPH 就采用了这种算法。
由于 RS 算法应用较广,有许多比较出名的开源实现如:
- Jerasure
- ISA-L
RS 算法的核心思路在于将原始数据分为 K 份大小相同的数据块,并根据这些数据块计算出 M 份大小相同的校验块。 将所有的数据块和校验块分别存储在不同的节点中,当有任意块丢失时,只要保证有任意 K 块存在,则可以将数据计算恢复。
- 编码流程
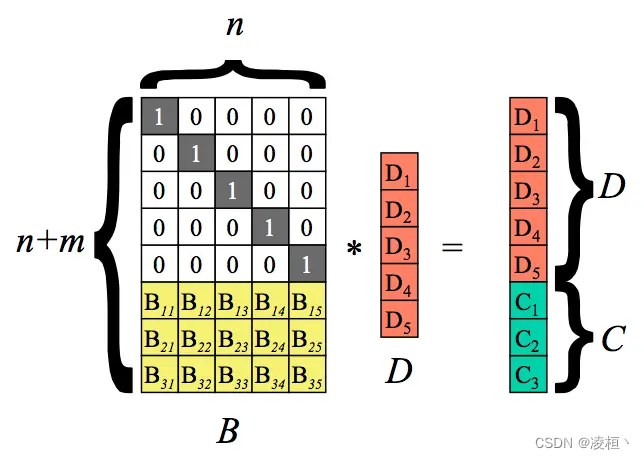
RS 编码流程
以 RS(5,3) 为例。如上图,首先会生成一个 n * (n + m) 大小的编码矩阵。矩阵有两部分组成,上半部分是一个 n * n 的单位矩阵,下半部份是一个 m * n 大小的校验矩阵(通常使用范德蒙矩阵或柯西矩阵)。通过将数据块和编码矩阵相乘,即得到一个 (n + m) * 1 的结果矩阵。其中数据块不变,生成 m 个校验块。
下面以范德蒙矩阵为例,这里简单描述一下解码流程,不涉及矩阵计算和代数原理。(感兴趣的可以研究下线性代数)
- 解码流程
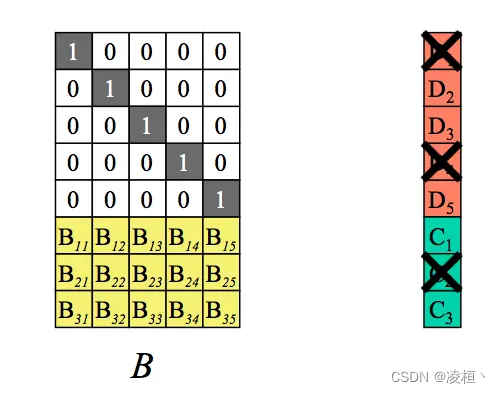
以之前的数据距离,假设同时丢失了 m 个块——D1、D4、C2。
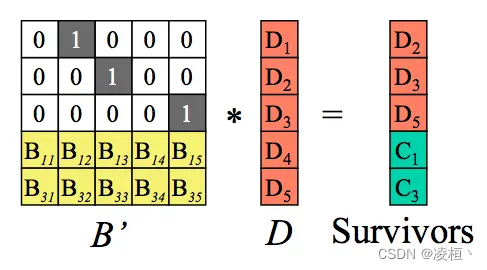
此时需要从编码矩阵中删除掉丢失块对应的行,生成新的编码矩阵与结果矩阵。
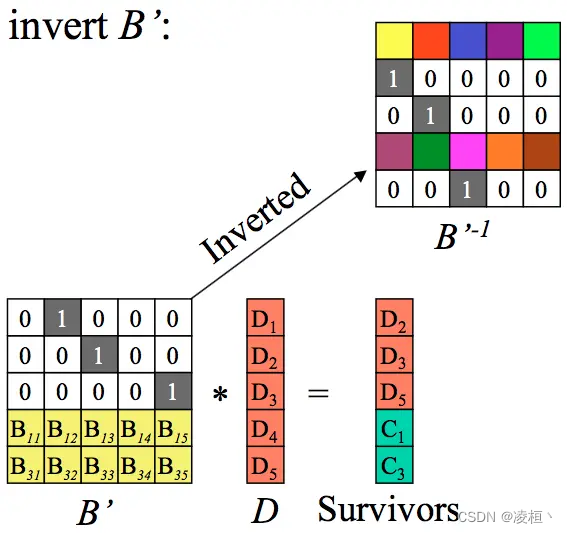
紧接着计算出编码矩阵的逆矩阵。
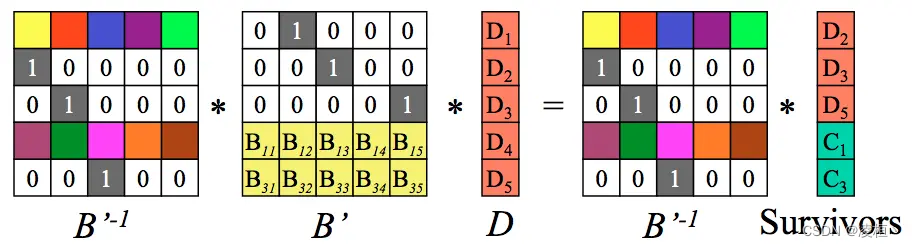
同时对等式两边乘以逆矩阵。
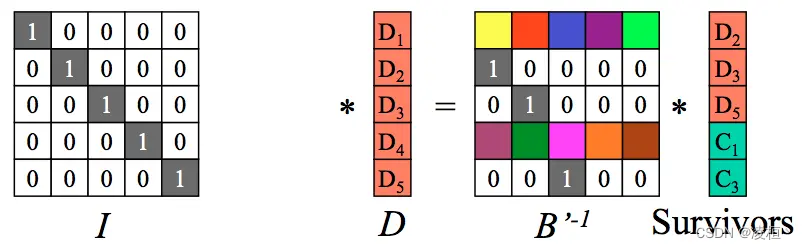
编码矩阵与逆矩阵相乘后得到单位矩阵。
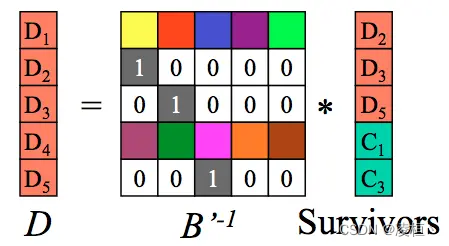
经过化简,此时得到原始数据 D,完成数据恢复。从上面的编解码流程可以看出,若要保证数据恢复,至多可丢失 M 个块(即删除 M 列不会影响矩阵计算)。
LRC
RS 虽然带来了大量的空间节省,但数据恢复的开销也急剧增大。当单数据块出现故障时,需要从 N 个节点上读取数据进行计算恢复。为了进一步降低恢复开销,Microsoft Azure 牺牲了部分空间,在 RS 的基础上封装出新的纠错算法 LRC(Locally Repairable Codes)。
LRC 算法的核心思路是将校验块拆分为全局校验块和局部校验块。 根据 K 个数据块计算出 M 个全局校验块,再将数据块平均分为 L 组,每组计算出一个局部数据块。
具体的原理这里不进行介绍,如果感兴趣可以去看看论文 Locally Repairable Codes
根据块类型的不同,数据恢复的开销也不一样:
- 数据块:
- 单数据块丢失时,需要同组其他数据块和局部校验块进行恢复。
- 多数据块丢失时
- 同组:如果丢失的是同组的数据块,则需要根据所有剩余的数据块和全局校验块进行恢复。
- 不同组:假设丢失的 N 个数据块处于不同组,则与单数据块流程一样,每组分别进行恢复。
- 全局校验块:需要根据所有的数据块进行恢复。
- 局部校验块:局部校验块丢失时,需要读取对应组的所有数据块进行恢复。
根据丢失的块类型,容错如下:
- 允许所有的校验块同时丢失。
- 允许 M 个块同时丢失。
SHEC
与 LRC 不同,CEPH 团队选择通过牺牲部分可靠性,近一步提高空间利用率,在 LRC 的基础上再次封装出新的纠错算法 SHEC(Shingled Erasure Code)。
SHEC 算法的核心思路是利用类似于滑动窗口的机制,每个校验块不仅包含对应数据块的信息,还包含上一个校验块的部分信息,因此某个校验块丢失时,也可以通过其他校验块进行恢复。 根据 K 个数据块,生成 M 个校验块,每个校验块中包含 C 个数据块。
具体的原理这里不进行介绍,如果感兴趣可以去看看论文 Erasure Code with Shingled Local Parity Groups for Efficient Recovery from Multiple Disk Failures
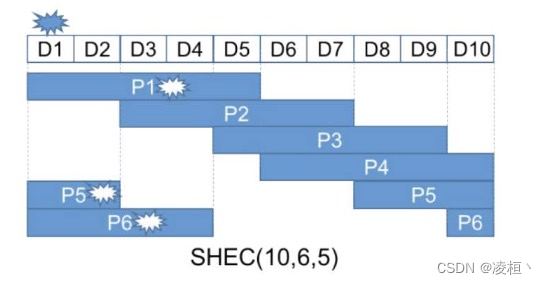
以上图 SHEC(10,6,3) 为例,即有 10 个数据块,6个滑动窗口,每个滑动窗口长度为 5。假设 D1 丢失时,我们可以通过读取 D2 ~ D5、P1 来进行数据恢复。而当 D6 和 D9 丢失时,可以通过读取同时包含这两个数据块的 P3、P4 校验块,以及 D5、D7、D8、D10 数据块,即可将数据恢复。
因此当一个数据块丢失时,仅需要读取 C 个数据块即可将数据恢复,并且同时支持丢失 (M * C) / K 个数据块丢。
总结
| 算法 | 多副本 | RS(K,M) | LRC(K,M,L) | SHEC(K,M,C) |
|---|---|---|---|---|
| 恢复开销(单数据块) | 1 | K | L | C |
| 空间开销 | N | (K + M) / K | (K + M + M / L ) / K | K + M |
| 容错上限 | N - 1 | M | M | M * C / K |
| 适用场景 | 小文件、热点文件 | 大文件、冷数据 |
- 应用场景
- 多副本保证了高可靠性以及低恢复开销,牺牲了空间。因此通常适用于高频访问的热点文件和小文件。
- 纠错码降低了空间开销,但是带来了容错损耗和编解码开销。因此通常适用于大文件及冷数据。
- 对比
- 空间利用率:RS > SHEC > LRC > 多副本
- 恢复速度:多副本 > LRC ≈ SHEC > RS
- 可靠性:多副本 > RS ≈ LRC > SHEC
