当前位置： 首页 > article >正文

C++算法之双指针、BFS和图论

article 2024/11/15 13:43:38

一、双指针

1.AcWing 1238.日志统计

分析思路

前一区间和后一区间有大部分是存在重复的
我们要做的就是利用这部分 来缩短我们查询的时间
并且在使用双指针时要注意对所有的博客记录按时间从小到大先排好顺序
因为在有序的区间内才能使用双指针记录两个区间相差
相当于把一个有序的时间序列进行每次递增1的划分

代码实现
#include<iostream>
#include<algorithm>

#define x first
#define y second
using namespace std;
const int N=100010;
typedef pair<int,int>PII;
PII logs[N];
bool st[N];
int cnt[N];
int main()
{
    int n,d,k;
    cin>>n>>d>>k;
    for(int i=0;i<n;i++) cin>>logs[i].x>>logs[i].y;
    
    sort(logs,logs+n);
    for(int i=0,j=0;i<n;i++)
    {
        int t=logs[i].y;
        cnt[t]++;
        
        while(logs[i].x-logs[j].x>=d)
        {
            cnt[logs[j].y]--;
            j++;
        }
        
        if(cnt[t]>=k) st[t]=true;
    }
    
    for(int i=0;i<100000;i++)
    {
        if(st[i]) cout<<i<<endl;
    }
    return 0;
}

2.AcWing 1240.完全二叉树的权值  

分析思路

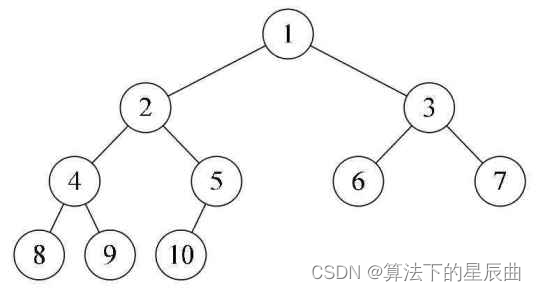
双指针：

从第一层根节点i=1，开始每一层开头都是2i,而每一层的长度就为pow(2,d-1)（d为层数）

前缀和：

因为是完全二叉树，所以算到最后要考虑是否越界。

代码实现

双指针

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N=100010;
int q[N];
LL sum[N];
int n,t;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&q[i]);
    LL m=-1e18;

    for(int i=1,d=1;i<=n;i*=2,d++)
    {
        LL s=0;
        for(int j=i;j<i+pow(2,d-1)&&j<=n;j++) s+=q[j];
        if(s>m)
        {
            m=s;
            t=d;
        }
    }

    cout<<t<<endl;
    return 0;
}

前缀和

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N=100010;
int q[N];
LL sum[N];
int n,t;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&q[i]);
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+q[i];
    LL m=-1e18;

    for(int i=1,d=1;i<=n;i*=2,d++)
    {
        LL s=0;
        LL r=i+pow(2,d-1)-1;

        if(r<=n) s=sum[r]-sum[i-1];
        else s=sum[n]-sum[i-1];

        if(s>m)
        {
            m=s;
            t=d;
        }
    }

    cout<<t<<endl;
    return 0;
}

二、BFS

1.AcWing 1101.献给阿尔吉侬的花束

分析思路

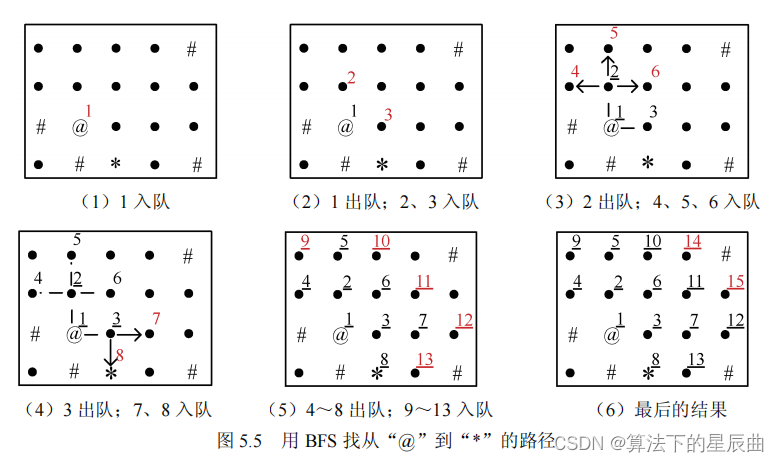
BFS广度优先遍历，就是队首出队，然后与队首相关的入队。上图为模拟过程！

代码实现
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N=210;

int n,m;
char g[N][N];
int dist[N][N];

int bfs(PII start,PII end)
{
    //队列
    queue<PII>q;
    memset(dist,-1,sizeof dist);//初始化距离为-1;
    
    dist[start.x][start.y]=0;
    q.push(start);
    
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    
    while(q.size())//队列不为空
    {
        auto t=q.front();//队首
        q.pop();
        
        //枚举四种方向上的情况
        for (int i = 0; i < 4; i ++ )
        {
            int x = t.x + dx[i], y = t.y + dy[i];
            if (x < 0 || x >= n || y < 0 || y >= m) continue;  // 出界
            if (g[x][y] == '#') continue;  // 障碍物
            if (dist[x][y] != -1) continue;  // 之前已经遍历过

            dist[x][y] = dist[t.x][t.y] + 1;

            if (end == make_pair(x, y)) return dist[x][y];

            q.push({x, y});
        }
    }
    
    return -1;
}

int main()
{
    int t;
    cin>>t;
    
    while(t--)
    {
        cin>>n>>m;
        for(int i=0;i<n;i++) scanf("%s",g[i]);//读入的是字符串,不需要加&
        
        PII start,end;//起点与终点
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(g[i][j]=='S') start={i,j};
                else if(g[i][j]=='E') end={i,j};
            }
        }
        
        int distance = bfs(start, end);
        if (distance == -1) puts("oop!");
        else printf("%d\n", distance);
    }
    return 0;
}

2.AcWing 1096.地牢大师

分析思路

二维上多加了一维，就有六个方向，读入用二维读入。

代码实现
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

struct Point
{
  int x,y,z;  
};

const int N=100;
char g[N][N][N];
int dist[N][N][N];
int l,r,c;
Point q[N * N * N];
int dx[6] = {1, -1, 0, 0, 0, 0};
int dy[6] = {0, 0, 1, -1, 0, 0};
int dz[6] = {0, 0, 0, 0, 1, -1};

int bfs(Point start,Point end)
{
    int hh=0,tt=0;
    q[0]=start;
    memset(dist,-1,sizeof dist);
    dist[start.x][start.y][start.z]=0;
    
    while(hh<=tt)
    {
        auto t=q[hh++];
        for(int i=0;i<6;i++)
        {
            int x=t.x+dx[i],y=t.y+dy[i],z=t.z+dz[i];
            
            if(x<0||y<0||z<0||x>=l||y>=r||z>=c) continue;
            if(g[x][y][z]=='#'||dist[x][y][z]!=-1) continue;
            
            dist[x][y][z]=dist[t.x][t.y][t.z]+1;
            if(g[x][y][z]=='E') return dist[x][y][z];
            
            q[++tt]={x,y,z};
        }
    }
    return -1;
    
}

int main()
{
    while(cin>>l>>r>>c,l||r||c)
    {
        Point start,end;
        for(int i=0;i<l;i++)
        {
            for(int j=0;j<r;j++)
            {
                scanf("%s",g[i][j]);//三维用两维来存
                for(int k=0;k<c;k++)
                {
                    if(g[i][j][k]=='S') start={i,j,k};
                    else if(g[i][j][k]=='E') end={i,j,k};
                }
            }
        }
        int distance=bfs(start,end);
        if(distance==-1) puts("Trapped!");
        else printf("Escaped in %d minute(s).\n",distance);
    }
    return 0;
}

用队列的方式： 

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

struct Point
{
  int x,y,z;  
};

const int N=100;
char g[N][N][N];
int dist[N][N][N];
int l,r,c;

int dx[6] = {1, -1, 0, 0, 0, 0};
int dy[6] = {0, 0, 1, -1, 0, 0};
int dz[6] = {0, 0, 0, 0, 1, -1};

int bfs(Point start,Point end)
{
    queue<Point> q;
    int hh=0;
    q.push(start);
    memset(dist,-1,sizeof dist);
    dist[start.x][start.y][start.z]=0;
    
    while(q.size())
    {
        auto t=q.front();
        for(int i=0;i<6;i++)
        {
            int x=t.x+dx[i],y=t.y+dy[i],z=t.z+dz[i];
            
            if(x<0||y<0||z<0||x>=l||y>=r||z>=c) continue;
            if(g[x][y][z]=='#'||dist[x][y][z]!=-1) continue;
            
            dist[x][y][z]=dist[t.x][t.y][t.z]+1;
            if(g[x][y][z]=='E') return dist[x][y][z];
            
            q.push({x,y,z});
        }
        q.pop();
    }
    return -1;
    
}

int main()
{
    while(cin>>l>>r>>c,l||r||c)
    {
        Point start,end;
        for(int i=0;i<l;i++)
        {
            for(int j=0;j<r;j++)
            {
                scanf("%s",g[i][j]);//三维用两维来存
                for(int k=0;k<c;k++)
                {
                    if(g[i][j][k]=='S') start={i,j,k};
                    else if(g[i][j][k]=='E') end={i,j,k};
                }
            }
        }
        int distance=bfs(start,end);
        if(distance==-1) puts("Trapped!");
        else printf("Escaped in %d minute(s).\n",distance);
    }
    return 0;
}


http://www.kler.cn/a/232883.html

相关文章：

  • 【月之暗面kimi-注册/登录安全分析报告】
  • 基于Spring Boot与Redis的令牌主动失效机制实现
  • 测试工程师简历「精选篇」
  • 远离生成式AI大乱斗，SAS公司揭示亚太区千亿AI市场蓝图
  • DevOps工程技术价值流：加速业务价值流的落地实践与深度赋能
  • python: postgreSQL using psycopg2 or psycopg
  • 【开源】基于JAVA+Vue+SpringBoot的假日旅社管理系统
  • 回溯算法:N皇后问题
  • 应用ANN+SMOTE+Keras Tuner算法进行信用卡交易欺诈侦测
  • JPEG图像的压缩标准（1）
  • 【蓝桥杯冲冲冲】Invasion of the Milkweed G
  • Excel——有效性、二级菜单联动
  • 【开源】JAVA+Vue+SpringBoot实现班级考勤管理系统
  • pytorch——保存‘类别名与类别数量’到权值文件中
  • python创建udf函数步骤
  • macbook电脑如何永久删除app软件?
  • java基础(2) 面向对象编程-java核心类
  • pytest+allure批量执行测试用例
  • Linux操作系统基础（三）：虚拟机与Linux系统安装
  • MATLAB环境下用于提取冲击信号的几种解卷积方法
  • 致我的2023年——个人学年总结
  • 32I2C通信协议
  • android 音频调试技巧
  • 25、数据结构/二叉树相关练习20240207
  • vue项目开发vscode配置
  • 《学成在线》微服务实战项目实操笔记系列（P1~P83）【上】