当前位置：首页 > article >正文

【EEG信号处理】对信号进行模拟生成

article 2024/11/14 2:40:38

生成信号的目的还是主要是为了学习和探究后面的分析方法；本文主要是对方法进行整理

瞬态 transient

瞬态信号是指的是一瞬间信号上去了，这种情况我们可以用在时域上高斯模拟

peaktime = 1; % seconds
width = .12;
ampl = 9;
gaus = ampl * exp( -(EEG.times-peaktime).^2 / (2*width^2) );

在这里插入图片描述

非稳态 Non-stationary

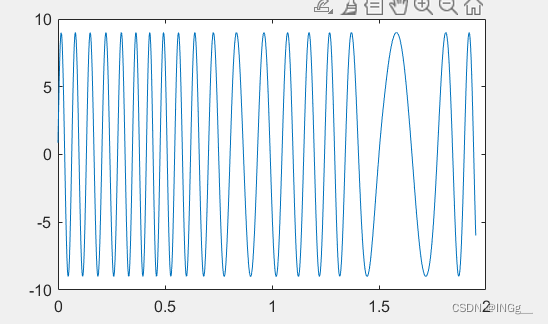
频率不成稳定的

freqmod = 5 + 20*interp1(rand(1,10),linspace(1,10,EEG.pnts)); % 范围5~25hz
signal  = ampl * sin( 2*pi * ((EEG.times + cumsum(freqmod))/EEG.srate) );

在这里插入图片描述

一些结合

持续的非稳态 ongoing non-stationary

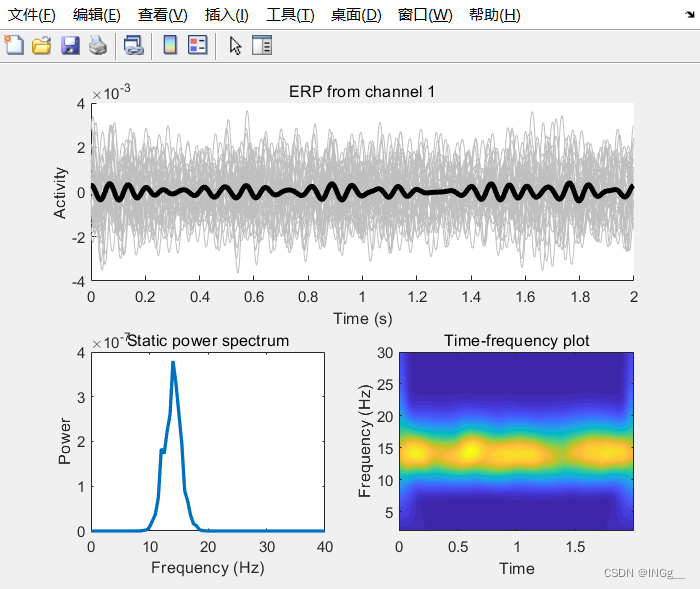
这种情况往往是需要生成窄带数据

创建窄带的非平稳数据，窄带非平稳依靠的是高斯分布两边的0，和生成在频率上的高斯分布，使得频率主要集中在峰上

% signal parameters in Hz
peakfreq = 14;
fwhm     =  5;


% frequencies
hz = linspace(0,EEG.srate,EEG.pnts);

%%% create frequency-domain Gaussian 生成频域高斯分布
s  = fwhm*(2*pi-1)/(4*pi); % normalized width
x  = hz-peakfreq;          % shifted frequencies
fg = exp(-.5*(x/s).^2);    % gaussian

% Fourier coefficients of random spectrum
fc = rand(1,EEG.pnts) .* exp(1i*2*pi*rand(1,EEG.pnts));
        
% taper Fourier coefficients by the Gaussian
fc = fg .* fc; % 将随机频谱的傅里叶系数与生成的窗口函数相乘；更像给高斯分布加了一点噪声

% go back to time domain to get EEG data
EEG.data(chani,:,triali) = real( ifft(fc) );

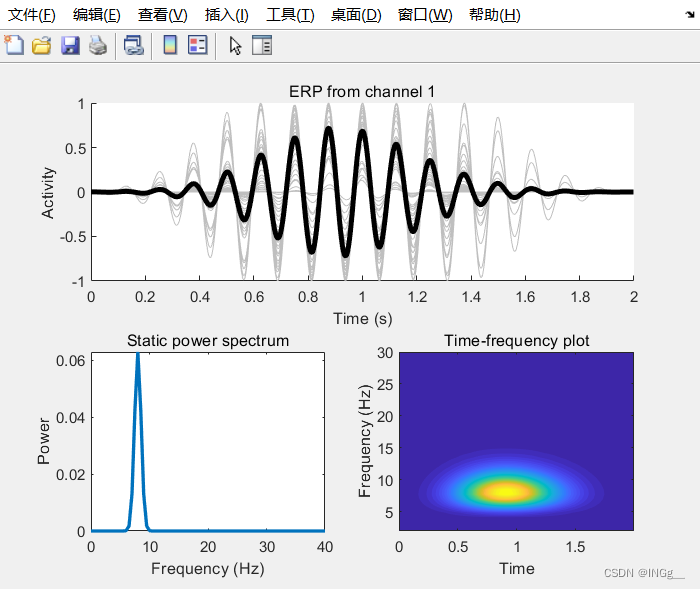
在这里插入图片描述

瞬时振荡信号 transient oscillations

瞬时还是利用高斯来实现，振荡就要利用到正弦来进行振荡了

% sine wave frequency
sfreq = 8;

% gaussian parameters (in seconds)
peaktime = 1;
width = .2;
trialpeak = peaktime + randn/5;
gaus = exp( -(EEG.times-trialpeak).^2 / (2*width^2) );


% generate sine wave with same phase
sw = cos(2 * pi * sfreq * EEG.times);


% data are sine wave times Gaussian
EEG.data(chani,:,triali) = sw .* gaus;

在这里插入图片描述

噪音

白噪声

% 可以直接用正态分布或者均匀分布来生成
randn(EEG.nbchan, EEG.pnts, EEG.trials);

粉噪声

% the key parameter of pink noise is the exponential decay (ed)
ed = 50;

% generate one-sided 1/f amplitude spectrum
as = rand(1,EEG.pnts) .* exp(-(0:EEG.pnts-1)/ed);
        
% Fourier coefficients as amplitudes times random phases
fc = as .* exp(1i*2*pi*rand(size(as)));
        
% inverse Fourier transform to create the noise
EEG.data(chani,:,triali) = real(ifft(fc));