蓝桥杯训练day3
day3
- 1.递推
- (1)3777. 砖块
- (2)95. 费解的开关
- (3)1208. 翻硬币
- 2.递归
- (1)1497. 树的遍历
- (2)97. 约数之和
1.递推
(1)3777. 砖块

思路:由于最终只有两种状态,全是B,全是W。
所以尝试两种情况。
对于全是B的情况:从字符串第一位开始,如果当前字符不是B,那么当前字符和下一个字符都变。然后同时记录当前字符的下标。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int T;
int n;
string str;
void update(char &c)
{
if(c=='W')c='B';
else c='W';
}
bool check(char c)
{
vector<int>res; //记录答案
string s=str;
int n=s.length();
for(int i=0;i<n-1;i++)
{
if(s[i]!=c)
{
update(s[i]);
update(s[i+1]);
res.push_back(i);
}
}
if(s.back()!=c)return false;
cout<<res.size()<<endl;
for(int i=0;i<res.size();i++)
cout<<res[i]+1<<" "; //为什么加1,因为题目规定下标从1开始
if(res.size())cout<<endl;
return true;
}
int main()
{
cin>>T;
while(T--)
{
cin>>n>>str;
if(!check('W')&&!check('B'))puts("-1"); //如果全白或者全黑都不行,输出-1
}
return 0;
}
(2)95. 费解的开关

思路:
首先明白规则,动一个数,他周围四个数和他本身都需要改变。
我们需要对其中的若干个数进行改变,且改变的的数不能超过6个。使最终所有数都变成1.
我们一行一行的点亮所有灯,前面层的点亮后再取点亮后面层的灯。如果当前四次灯都被点亮后,第五行的灯没有被点亮,那么则说明永远不能点亮。因为前4层都点亮了,此时去点亮第五层,第五层一动,第四层又会变化。每一层的0都应该由下一层操作来处理变成1,因为这样就不会影响到上一层已经处理好的1。
首先可以保证这样一层一层来点亮灯一定可以得到答案,只是步数不一定小于等于6.
那么要保证步数最小,这与什么有关呢??不知道。但是可以知道的是,无论是哪种操作方案,一旦决定了第一步,按照上面的定义,一层一层来递推,得到的答案是唯一的。而第一步就是对第一层操作。那么就穷举第一层的操作,然后固定第一层,从第二层开始去点亮上面一层的灯。
也许说的难懂。请看这个题解:
添加链接描述
#include<iostream>
#include<cstring>
using namespace std;
char g[10][10];
char backup[10][10];
int n;
void turn(int x,int y)
{
int dx[5]={0,-1,0,1,0};
int dy[5]={0,0,1,0,-1};
for(int i=0;i<5;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a<0||b<0||a>=5||b>=5)continue;
if(g[a][b]=='0')g[a][b]='1';
else g[a][b]='0';
}
}
int main()
{
cin>>n; //n组数据
while(n--)
{
//输入数据
for(int i=0;i<5;i++)cin>>g[i];
int ans=7;
//枚举第一行的所有开关选择方案
for(int k=0;k<1<<5;k++) //00000-11111 即一个都不按到全都按下。
{
int step=0;
memcpy(backup,g,sizeof g); //每次都将初始状态拷贝到“操作数组”
//看看第一行按了哪些个,并且需要按照规则改变周边的灯
for(int i=0;i<5;i++)
{
if((k>>i)&1) //1表示按,0表示不按
{
step++;
turn(0,i);
}
}
//上面固定第一行后,然后操作第二行,操作第二行使第一行都变成1.然后操作第三行,使第二行都变1
//一直操作到第5行,使第四行全变成1,最后第五行不能操作了,因为操作第五行会改变第四行已经
//是1的状态。最后判断第五行是否都是1,如果不是,则不能使灯泡全亮
bool ok=true;
for(int i=0;i<4;i++) //观察第i行,然后用i+1行取改变i行状态
{
for(int j=0;j<5;j++)
{
if(g[i][j]=='0')
{
step++;
if(step>6) //剪枝一下
{
ok=false;
break;
}
turn(i+1,j);
}
}
if(!ok)break;
}
if(ok)
{
int i=0;
for(i;i<5;i++)
if(g[4][i]=='0')break;
if(i==5)
ans=min(ans,step);
}
//记得还原备份
memcpy(g,backup,sizeof backup);
}
if(ans<=6)
cout<<ans<<endl;
else
cout<<"-1\n";
}
return 0;
}
(3)1208. 翻硬币
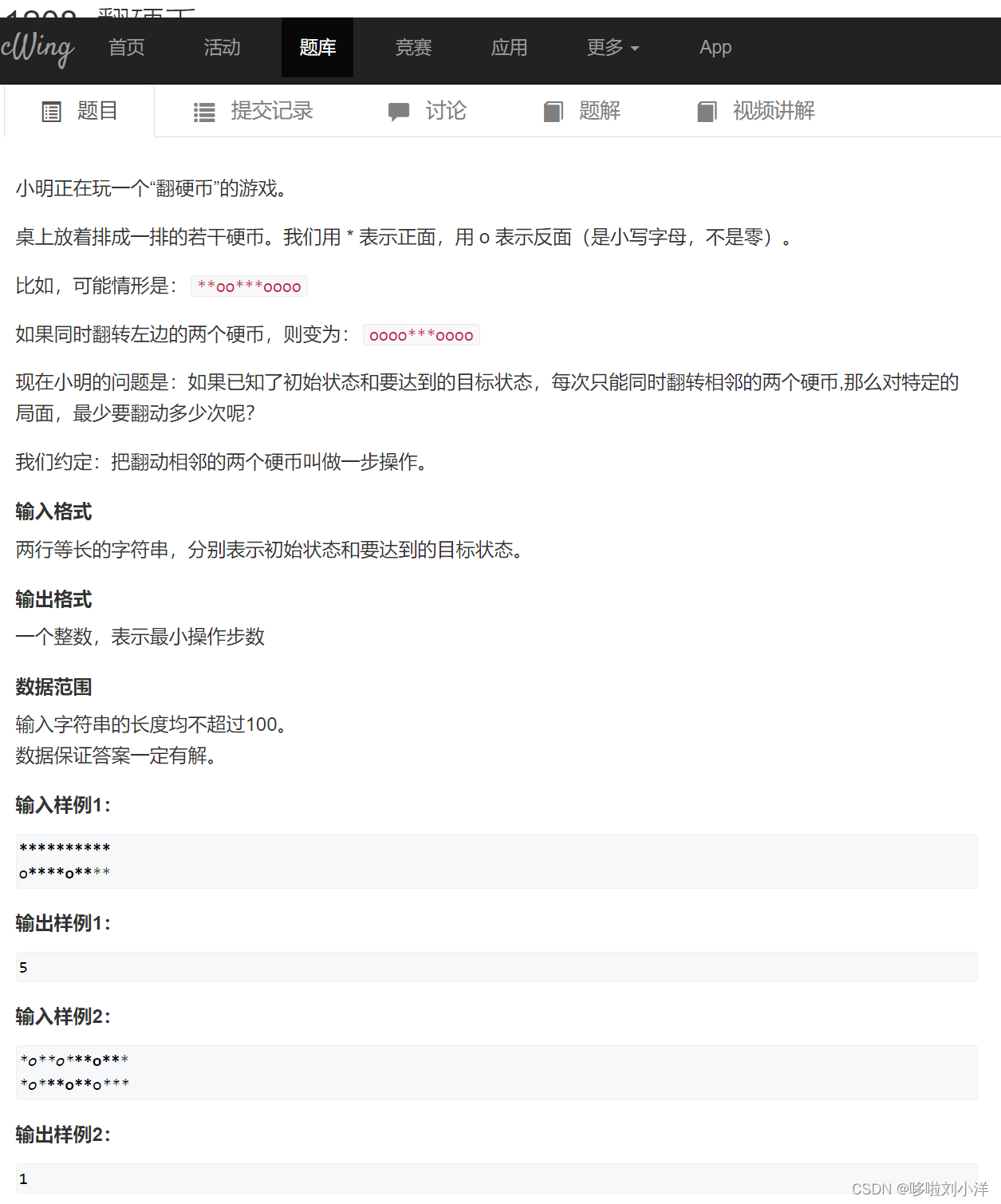
思路:
就近原则,遇到一样的就不变,遇到不一样的就翻转。贪心思想。为什么会得到最小哎,还没有证明。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
string start;
string target;
int ans;
void update(char& c)
{
if(c=='*')c='o';
else c='*';
}
int main()
{
cin>>start;
cin>>target;
//先尝试一下就近原则
int n=start.size();
for(int i=0;i<n-1;i++)
{
if(start[i]!=target[i])
{
update(start[i]);
update(start[i+1]);
ans++;
}
}
cout<<ans<<endl;
return 0;
}
2.递归
(1)1497. 树的遍历
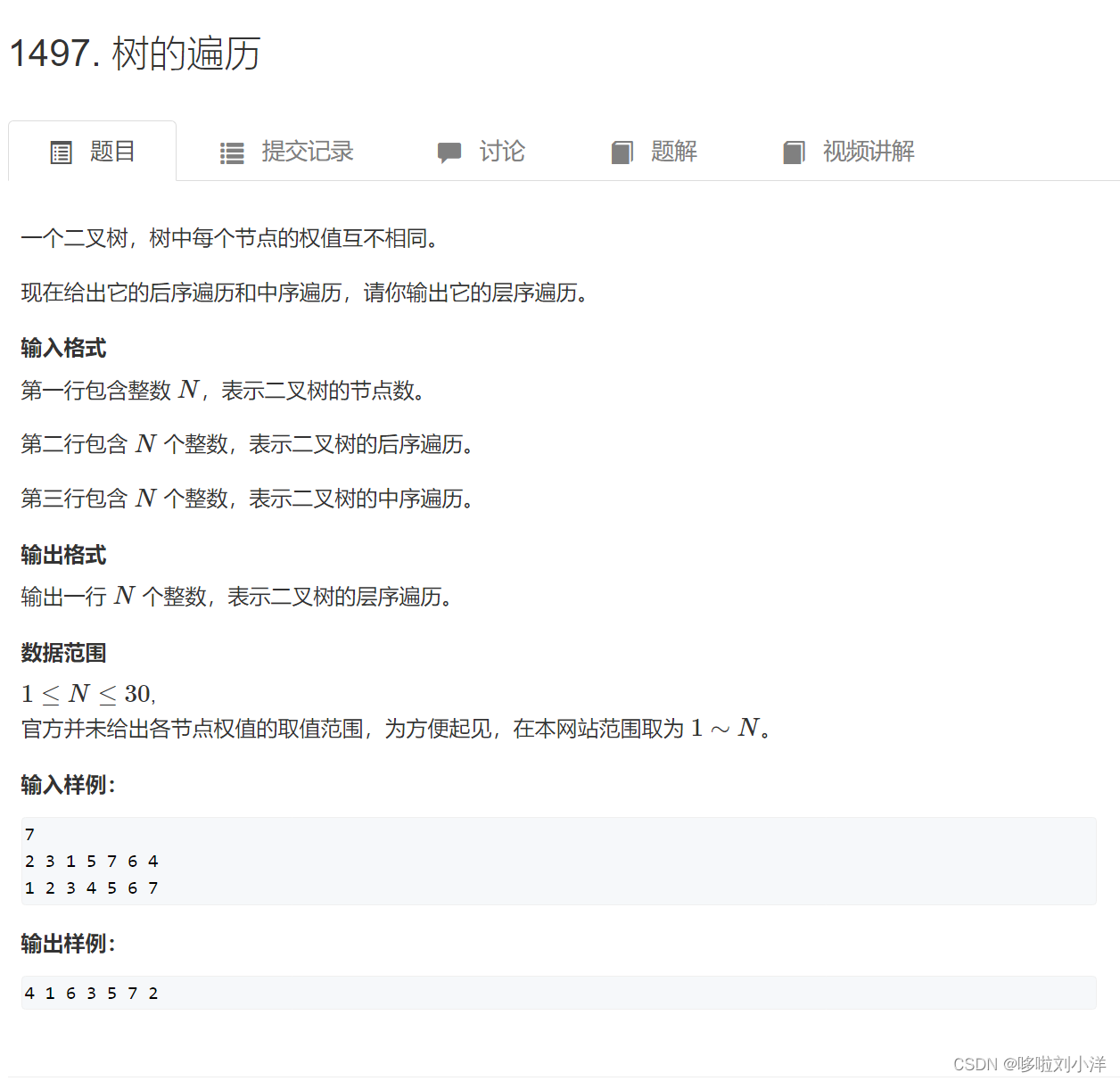
思路:经典二叉树问题,很入门的递归的题目,但是要手写非递归方式有点考验能力。
递归的小诀窍,尝试解决问题,往里面解决三层,然后发现规律,然后利用规律写递归方程。考虑边界情况和递归最底层的处理。
先构造,再遍历。
关键几点:
- 了解前中后序遍历的规则
- 了解递归的本质:重复做步骤一样的事情,搭建好框架。
- 理解层次遍历的规则,结合队列的性质,层次遍历可以用队列的性质来实现
- 比较难理解的一点:找区间(就是l1-k-1-…那些)
#include<iostream>
#include<cstring>
#include<unordered_map>
using namespace std;
const int N=31;
int postorder[N],inorder[N];
unordered_map<int,int>lchild; //记录树的节点(层次遍历) lchild[i]=j表示i的左孩子是j
unordered_map<int,int>rchild; //同理
unordered_map<int,int>Hash; //存储中序遍历每个节点的下标
int n;
int dfs(int l1,int r1,int l2,int r2) ///[l1,r1]表示中序遍历的区间,[l2,r2]表示后续遍历的区间
{
if(l1>r1)return 0;
int root=postorder[r2]; //根节点
int k=Hash[root]; //根节点在中序遍历里面的位置
lchild[root]=dfs(l1,k-1,l2,l2+(k-1-l1)); //构造左孩子 [中左,中右,后左,后右](k-1-l1)表示的是左孩子的长度-1,l2+上它就表示左孩子的右端点
rchild[root]=dfs(k+1,r1,l2+(k-1-l1)+1,r2-1); //构造右孩子
return root;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
cin>>postorder[i];
for(int i=0;i<n;i++)
{
cin>>inorder[i];
Hash[inorder[i]]=i; //这一步是后面的一个优化过程,一开始不理解很正常
}
int root=dfs(0,n-1,0,n-1); //找到根节点
int q[N];
int hh=0,tt=-1;
if(root) //找到根节点
q[++tt]=root;
while(hh<=tt) //实际上队列的行为正好符号层次遍历的规则
{
int t=q[hh++];
//看当前节点的左右孩子节点是否存在
if(lchild[t])
q[++tt]=lchild[t];
if(rchild[t])
q[++tt]=rchild[t];
}
for(int i=0;i<=tt;i++)
cout<<q[i]<<" ";
return 0;
}
(2)97. 约数之和
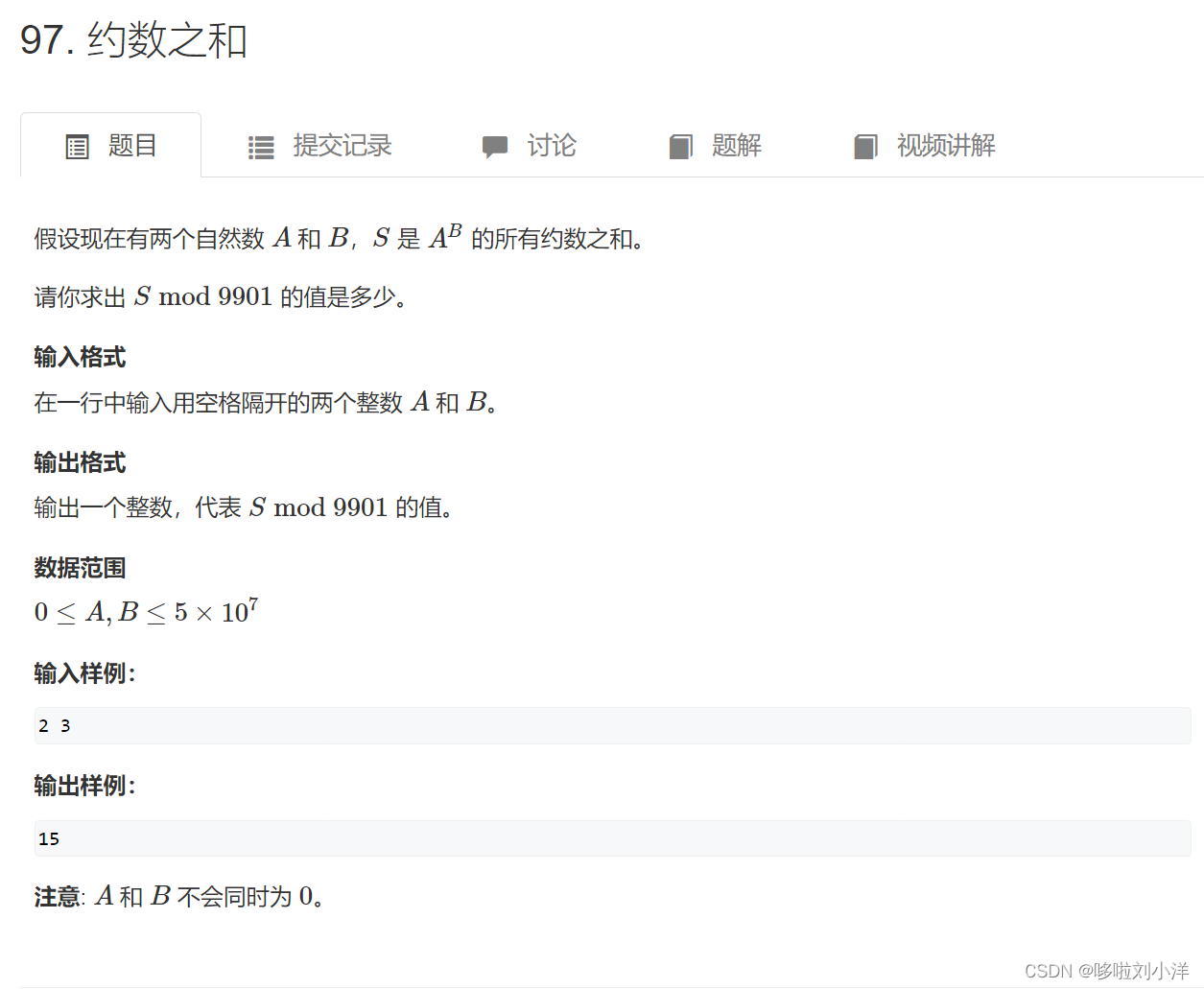
这道题需要用到一些数学基础知识,否则写的很困难。可以参考一下:
- 试除法求约数
- 筛选质因数
- 约数之和
- 约数个数
- 快速幂
- 秦九邵算法
过程比较复杂,需要做好一写就一天的思想准备,一步一步来,巩固基础,然后做出这道题。
#include<iostream>
#include<cstring>
#include<cmath>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int mod=9901;
ll res=1;
unordered_map<int,int>Hash;
ll qmid(ll a,ll b) //a的b次幂
{
ll ans=1;
while(b)
{
if(b&1)
ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
ll sum(int p,int k) //递归求和,等价于其他方式,可能速度快一点,因为用到了快速幂
{
if(k==1)
return 1;
if(k%2==0)
return (qmid(p,k/2)+1)*sum(p,k/2)%mod;
else
return (qmid(p,k-1)+sum(p,k-1))%mod;
}
int main()
{
int a,b;
cin>>a>>b;
//第一步,分解a,将其变为质因数的幂次相乘
int t=a;
for(int i=2;i<=t/i;i++) //筛选质因数
{
while(t%i==0)
{
Hash[i]++;
t/=i;
}
}
if(t>1)Hash[t]++;
//第二步:求值
for(auto prime:Hash)
{
ll x=prime.first;
ll y=prime.second*b;
res=res*sum(x,y+1)%mod;
}
if(a==0)res=0;
cout<<res<<endl;
return 0;
}
