当前位置：首页 > article >正文

0x03数学预备

article 2025/1/11 6:54:28

线性代数

标量

实质上就是一个点或者说是一个零维的ndarary

x = torch.tensor(3.0)
y = torch.tensor(4.0)

x + y, x * y, x / y, x ** y, x > y

向量

向量基本运算遵循广播机制，对应的点相加减，相乘除，长度是L2范数

在大量文献中，列向量为向量的默认方向

长度、维度、形状

长度：长度为n等价于有几个元素

维度：向量或轴的元素数量

形状：几维几维

矩阵

正定矩阵： $x^TAx \geq 0$

转置操作：交换矩阵的行和列

A.T

计算

向量点积

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

# (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))

踩个坑：点积要求类型一样

矩阵乘向量

在这里插入图片描述

注意函数不一样（Matrix Vector Multiplication）

矩阵乘矩阵

遵循线代中的矩阵乘法

B = torch.ones(4, 3)
torch.mm(A, B)

tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

求范数

范数通常用来代表特征之间的距离来表示样本之间的相似度

L2范数

u = torch.tensor([3.0, -4.0])
torch.norm(u)

L1范数

torch.abs(u).sum()

F范数，在矩阵中用的比较多

torch.norm(torch.ones((4, 9)))

张量

# 更多的轴
X = torch.arange(24).reshape(2, 3, 4)

tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11]],

        [[12, 13, 14, 15],
         [16, 17, 18, 19],
         [20, 21, 22, 23]]])
# 仔细观察2 3 4都是什么
# 在1个三维张量中，有2个二维矩阵，每个二维矩阵有3个向量，每个向量有4个标量

计算

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()
A, A + B, A * B

注意，这里的加减乘除都是对应元素的加减乘除，并非完全按照矩阵运算来做

这里的按元素乘法也称为哈达玛积

这里的A也可以是标量，一样转化为对矩阵每个元素进行加减

求和

sum函数进行求和

当sum后不带参数的话最好理解的，也就是对所有元素进行求和

首先需要明确的是，axis是怎么确定的。以三维来举例，[2, 4, 5]（这个就可以用shape来查看），0代表是第一个维度，也就是行

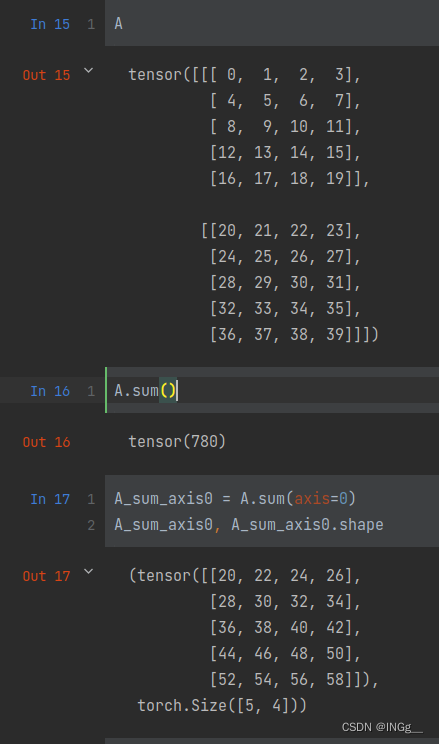
在这里插入图片描述

观察一下，按照行对应的元素，对应元素相加，对张量拍扁了0+20, 1+21....

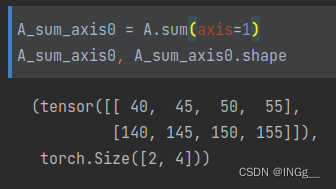
在这里插入图片描述

同样的，按照列求了和，剩下的维度就是[2, 4]

如果多维求和的话，简单理解就是去掉其他的轴；形象的理解就是按照顺序依次求和

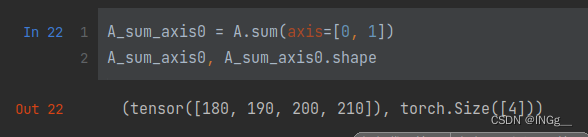
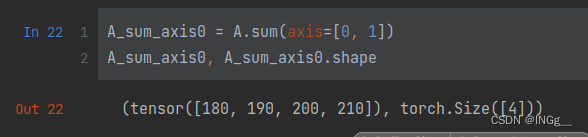
在这里插入图片描述

比如说，前面已经算过axis=0的时候的结果了（往上数第三张图），再按照已经算出来的结果再讲其按照另一个还没算的维度，也就是此时是新得到的矩阵的行压缩，列求和

保持维度加上参数keepdims=True，目的是方便跟广播

A_sum_axis0 = A.sum(axis=[0, 1], keepdims=True)
A_sum_axis0, A_sum_axis0.shape

# (tensor([[[180, 190, 200, 210]]]), torch.Size([1, 1, 4]))

累加操作：

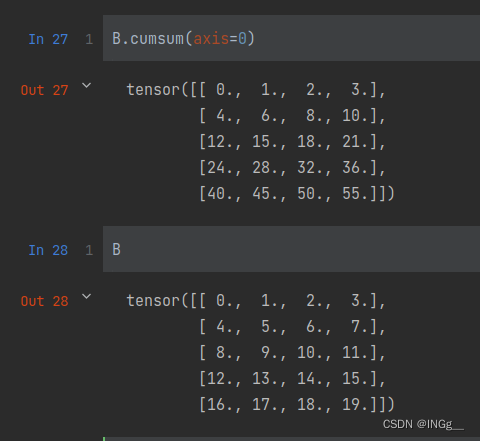
在这里插入图片描述

形象的来看实际上是一种前缀和

微积分

标量求导

就是常见的求导方式

在这里插入图片描述

亚导数：求导扩展到不可微的情况下

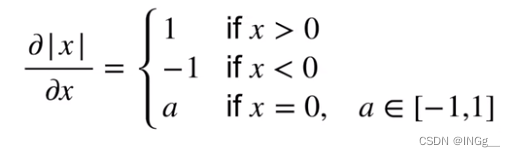
在这里插入图片描述

这时候a可以在-1到1之间取任意值

梯度

导数扩展到向量

连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量

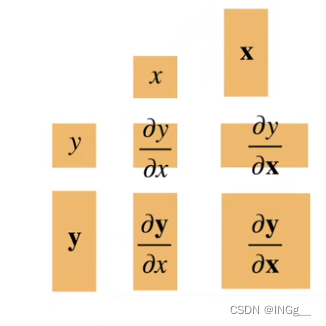
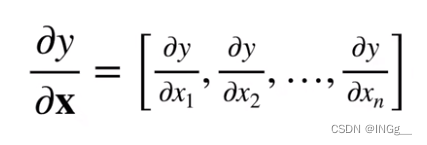
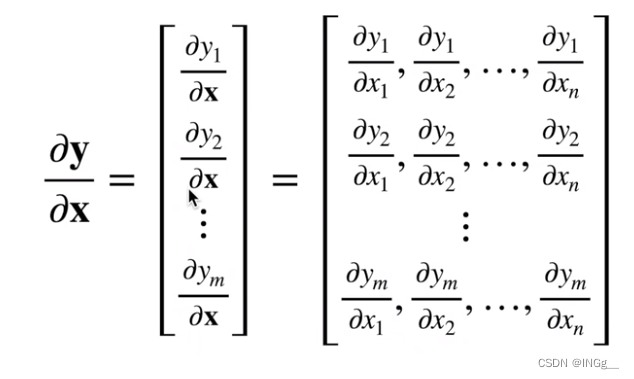
在这里插入图片描述

微分多元函数求导法则

标量对向量求导：

在这里插入图片描述

向量对向量求导：

在这里插入图片描述

自动求导

理论

解释自动求导之前需要先进行链式法则来进行整理

先将函数一步步的拆分，然后逐个求导。

标量的求导还是比较好理解的，例子如下，使用的是线性回归的例子：

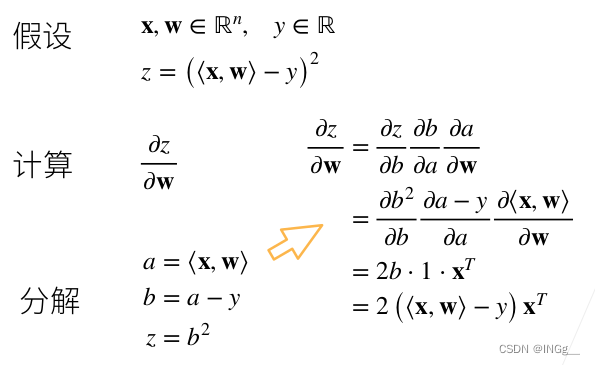
在这里插入图片描述

这里可以解释x是行向量，w是列向量，内积对列向量求导还是列向量，而x是行向量，所以取转置

矩阵的求导需要借助上面几个图的公式来进行

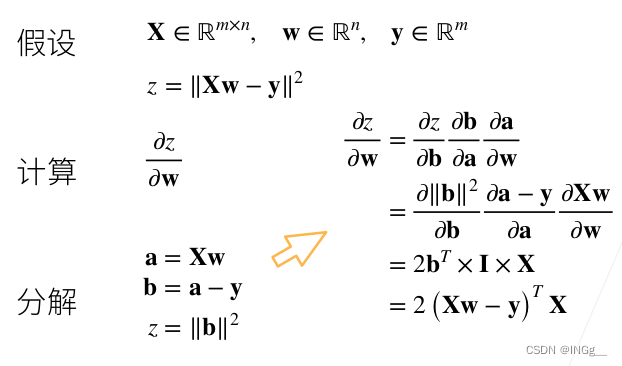
在这里插入图片描述

在自动求导中，使用反向累积（反向传播）相比正向传播的好处是能够节省内存，不需要在正向的过程中读取之前的结果，同时如果不需要求其中某个变量的导数也可以相应的减少计算量

正向就是求复合函数的值，反向就是求偏导数和梯度，数学中的求导就是反向传播的求导方向

实践

x = torch.arange(4.0)

x.requires_grad_(True) # 用来声明存储梯度的空间
print(x.grad) # 一开始默认为None

y = 2 * torch.dot(x, x) # 随便创建一个函数做实验 y = 2(x1*x1 + x2 * x2 + ...)
y

y.backward()
x.grad # 得到的结果我们通过数学知识知道应当为 4x
# tensor([ 0.,  4.,  8., 12.])

x.grad == 4 * x
tensor([True, True, True, True])

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()


x.grad.zero_()
y = x * x
u = y.detach() # detach就是让新创建的变量不对x求梯度，把y看做常数
z = u * x

z.sum().backward()
x.grad == u
tensor([True, True, True, True])

控制流的梯度计算

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()