当前位置：首页 > article >正文

链式二叉树--前序中序后序遍历，高度，节点个数问题

article 2025/1/30 16:42:04

前言：

一：链式二叉树的结构定义

二：链式二叉树的遍历--->前序，中序，后序

1.前序

递归展开图分析

2.中序

递归展开图分析

3.后序

三：二叉树结点的求解

1.二叉树总结点

递归展开分析

2.二叉树叶子结点数

递归展开分析

3.二叉树第k层节点个数

递归展开分析

四：二叉树的高度

五：总结语

接下来的日子会顺顺利利，万事胜意，生活明朗-----------林辞忧

前言：

链式二叉树作为后续AVL树，B系列树的雏形，理解掌握链式二叉树的各种操作很重要，此处就需要用递归来实现链式二叉树的各种操作，相信认真学习过后会对递归有更深刻的理解，接下来我们就开始上菜

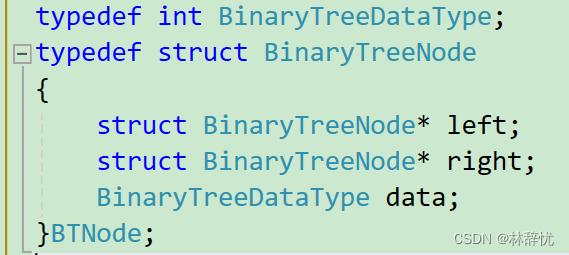
一：链式二叉树的结构定义

链式二叉树的结构由指针域和数值域组成，况且链式二叉树并不都是完全二叉树，还有普通二叉树，每个节点最多两个孩子

二：链式二叉树的遍历--->前序，中序，后序

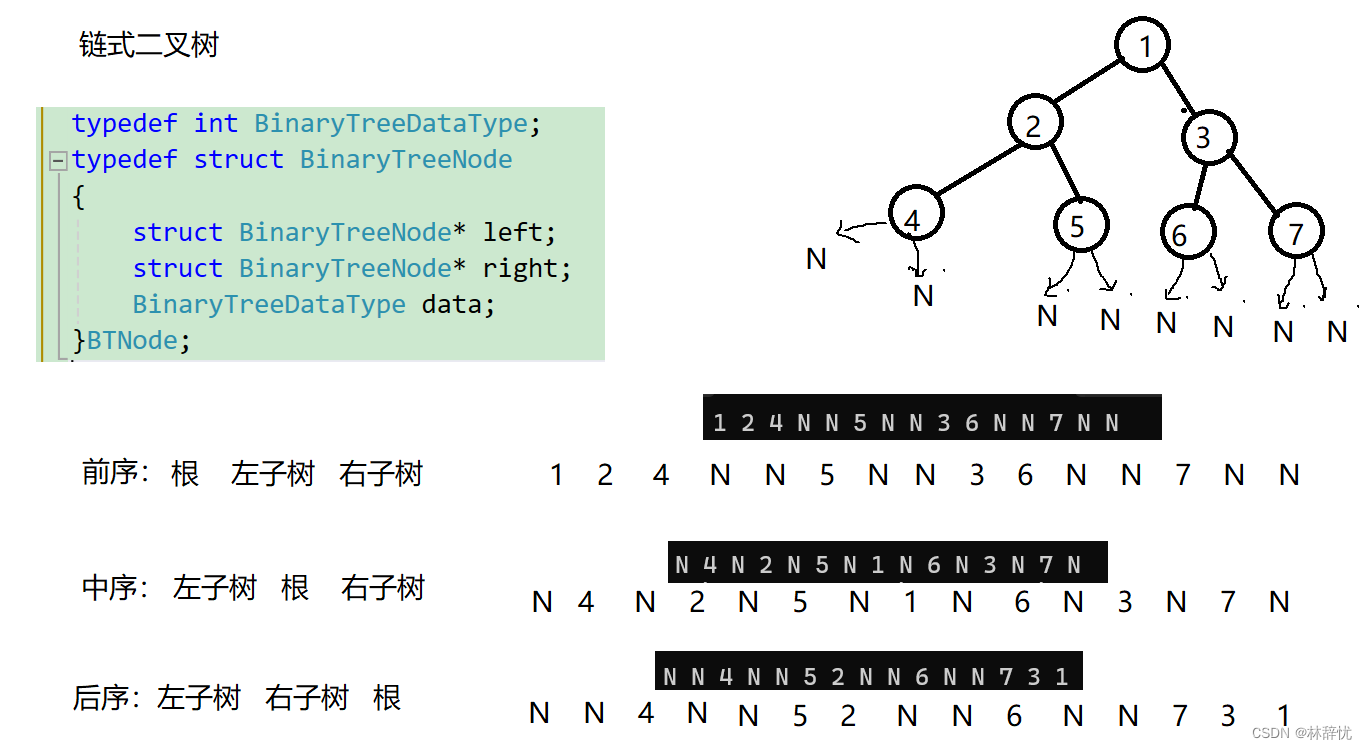
1.前序

BTNode* Buynode(int x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail\n");
		return NULL;
	}
	newnode->left = NULL;
	newnode->right = NULL;
	newnode->data = x;
	return newnode;
}

BTNode* CreatTree()
{
	BTNode* n1 = Buynode(1);
	BTNode* n2 = Buynode(2);
	BTNode* n3 = Buynode(3);
	BTNode* n4 = Buynode(4);
	BTNode* n5 = Buynode(5);
	BTNode* n6 = Buynode(6);
	BTNode* n7 = Buynode(7);

	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;
	n3->left = n6;
	n3->right = n7;

	return n1;
}
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return ;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

递归展开图分析

2.中序

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

递归展开图分析

3.后序

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

后续递归展开图同上展开即行

三：二叉树结点的求解

1.二叉树总结点

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)//递归结束条件
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//从左子树和右子树中分别计数
}

递归展开分析

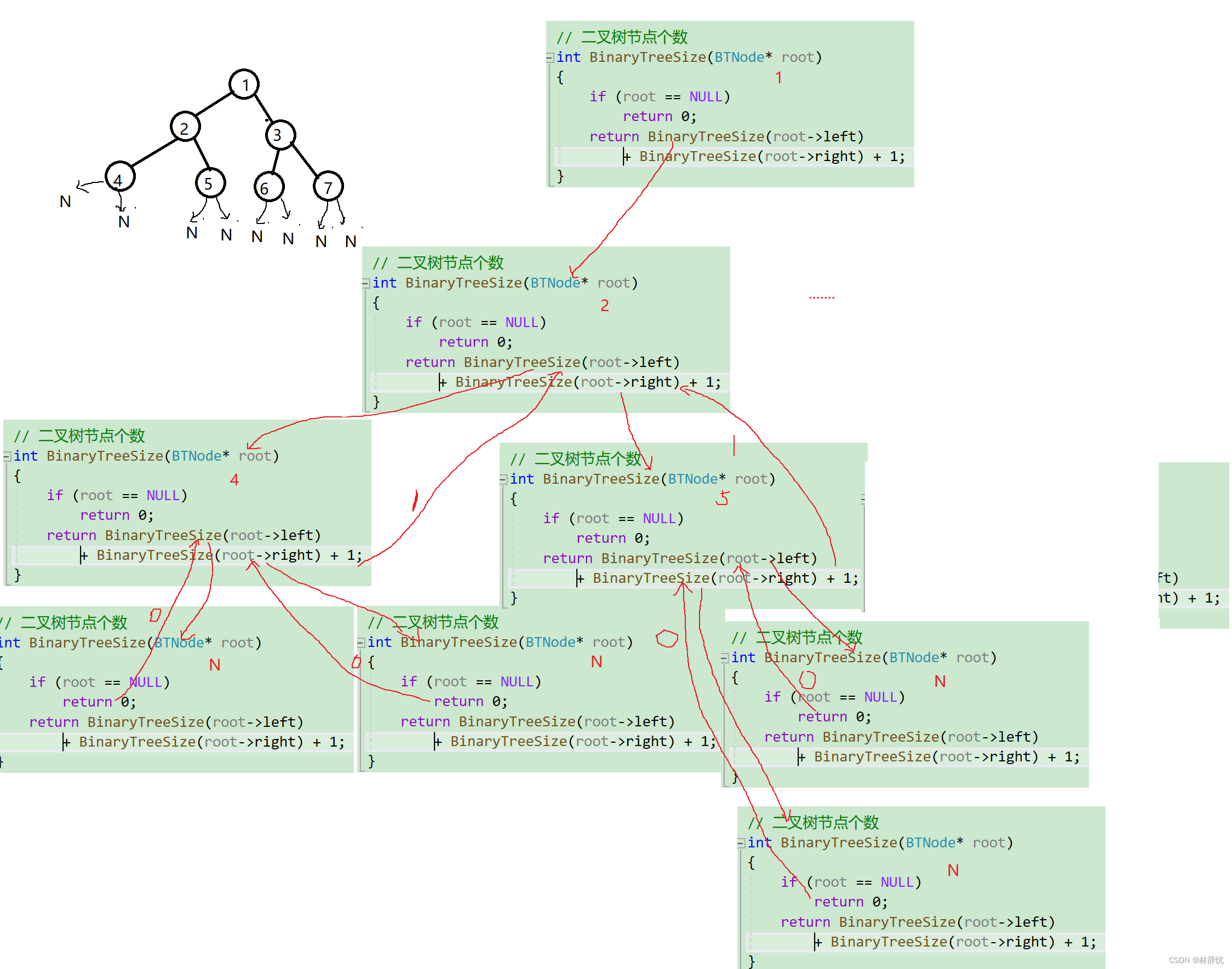
2.二叉树叶子结点数

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)//空树返回0
		return 0;
	if (root->left == NULL && root->right == NULL)//叶子节点无孩子
		return 1;
	return BinaryTreeLeafSize(root->left)//递归往下寻找 
		+ BinaryTreeLeafSize(root->right);
}

递归展开分析

3.二叉树第k层节点个数

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)//循环走到k==1时停止，且不为空
		return 1;
	//分治思想：转化为求k-1层的节点数
	return BinaryTreeLevelKSize(root->left, k - 1) 
		+ BinaryTreeLevelKSize(root, k - 1);
}

递归展开分析

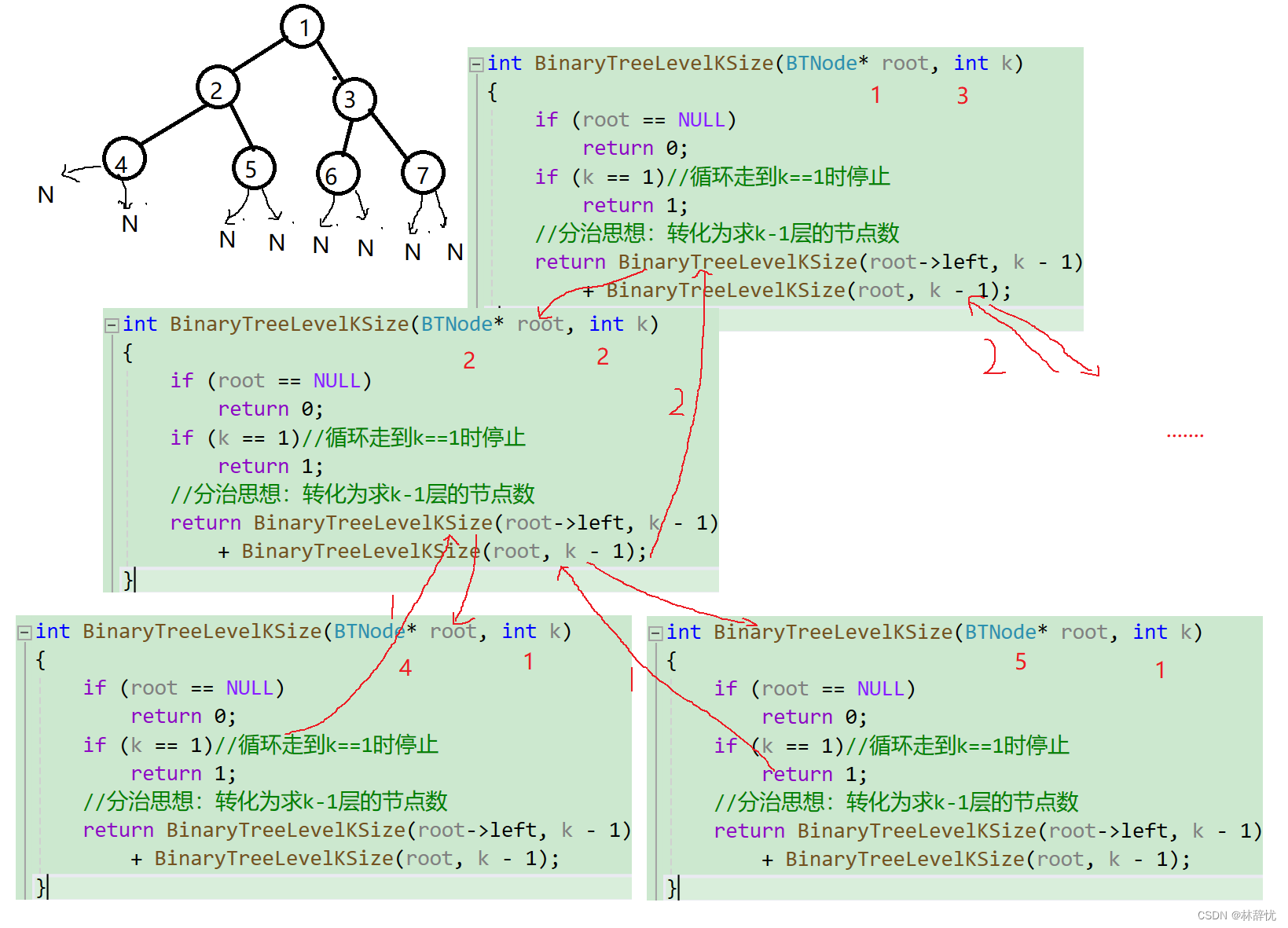
四：二叉树的高度

//二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
   //记录左右长度，再进行比较
	int leftHeight = BinaryTreeHeight(root->left);
	int rightHeight = BinaryTreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

此图递归展开图就省略了昂