算法笔记p154最大公约数和最小公倍数

最大公约数

正整数a与b的最大公约数是指a与b的所有公约数中最大的那个公约数，一般用gcd(a, b)表示a和b的最大公约数。

辗转相除法

1. 设a、b均为正整数，则gcd(a, b) = gcd(b, a % b)。
2. 即被除数和除数的最大公约数与除数和他们的余数的最大公约数相等。

证明

• 设a = kb + r，其中k和r分别为a除以b得到的商和余数。
• 则有r = a - kb成立。
• 设d为a和b的一个公约数。
• 那么由r = a - kb，得d也是r的一个公约数。
• 因此d是a和r的一个公约数。
• 又由r = a % b，得d为b和a % b的一个公约数。
• 因此d既是a和b的公约数，也是b和a % b的公约数。
• 由d的任意性，得a和b的公约数都是b和a % b的公约数。
• 由a = kb + r，同理可证b和a % b的公约数都是a和b的公约数。
• 因此a和b的公约数与b和a % b的公约数全部相等，故其最大公约数相等。
• 即有gcd(a, b) = gcd(b, a % b)。
• 证毕

例子

• a = 24，b = 36，a % b = 24，gcd(24，36) = gcd(36，24)
• a = 36，b = 24，a % b = 12，gcd(36，24) = gcd(24，12)
• a = 24，b = 12，a % b = 12，gcd(24，12) = gcd(12，12)
• a = 12，b = 12，a % b = 0，gcd(12，12) = gcd(12，0) = 12
• 0和任意一个整数a的最大公约数都是a（注意：不是0）。

代码实现

可以发现，当a ＜ b时，辗转相处的操作的结果就是将a和b交换；当a ＞ b时，辗转相处的操作可以让a减小得非常快，当b为0时，得到最大公约数。因此，可以想到递归实现：

• 递归式：gcd(a, b) = gcd(b, a % b)。
• 递归边界：gcd(a, 0) = a。

int gcd(int a, int b) {
    if (b == 0) return a;
    else return gcd(b, a % b);
}

用三目运算符：

int gcd(int a, int b) {
    return !b ? a : gcd(b, a % b);
}

最小公倍数

• 正整数a与b的最小公倍数是指a与b的所有公倍数中最小的那个公倍数，一般用lcm(a, b)表示a和b的最小公倍数。
• 当得到a和b的最大公约数d时，可以马上得到a和b的最小公倍数为ab/d，这个公式通过集合可以快速理解。
  
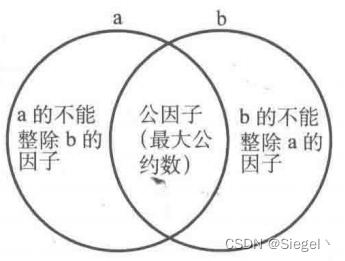
• 由图很容易发现，a和b的最大公约数即集合a与集合b的交集，而最小公倍数为集合a与集合b的并集。
• 要得到并集，由于ab会使公因子部分多计算一次，因此需要除掉一次公因子,于是就得到了a与b的最小公倍数为ab/d。
• 由于ab在实际计算时有可能溢出，因此更恰当的写法是a/db。
• 由于d是a和b的最大公约数，因此a/d一定可以整除。

代码实现

int lcm(int a, int b) {
    return a / gcd(a, b) * b;
}