NSGA-III算法:如何在多目标优化问题中找到最合适的解
当我们面临多个目标函数时,单目标的遗传算法可能无法满足需求。这时,我们可以引入多目标遗传算法。在这种情况下,目标函数可能存在冲突,例如,一个目标函数需要最小化,而另一个目标函数需要最大化。某个目标函数的提高可能需要以另一个函数的降低为代价。这就引出了帕累托解(Pareto解)的概念。即每个目标都想达到最优。
解决pareto解有以下几种常用方法:
权重系数转换法
对于每个目标函数f(xi)(i=1,2,3,4…),赋予权重wi(i=1,2,3…),wi为目标函数重要程度,有
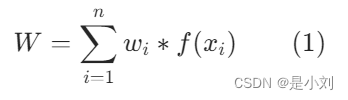
权重系数函数利用权重将多目标转化为单目标函数,将W作为评价函数。
缺点:需要自己确定特征数据的权重,主观影响较大。
排序选择法
基于pareto最优个体的概念对群体中的个体进行排序。然后根据这个次序进行种群选择。这样的话能够让pareto最优个体有更多的机会遗传到下一代。
缺点:仅仅度量了各个个体之间的优越次序,而并未度量各个个体的分散程度,所以容易生成相似的解,而不是分布较广的多个最优解。
带精英策略的非支配排序遗传算法–NSGAII
(1)采用快速非支配型排序,降低了算法复杂度。其复杂度为O(MN**2)。
(2)提出了拥挤度和拥挤度比较算子,代替需要制定共享半径的适应度共享策略。并在快速排序后的同级比较中作为胜出标准。使pareto解中的个体扩展到整个pareto域中,并均匀分布,保持了种群的多样性。
(3)引入精英策略,扩大采样空间。将父代种群和子代种群合并,保证优良个体能够留存下来。
算法步骤如下:
首先随机产生数量为n的初始种群
(2)然后对其进行非支配排序,,可以将种群中的个体按照pareto支配关系分成不同的层级。
(3)然后计算每个个体的拥挤度,拥挤度主要是用于衡量每个个体在目标空间中与其他个体的相似程度,拥挤度距离越大,说明个体越具有多样性。
(4)接下来,就是常规的选择,交叉,变异操作产生第一代子代种群。
从第二代开始,将父代和子代合并
然后对其进行快速非支配型排序,同时计算每个非支配层的个体进行拥挤度的计算。然后根据非支配关系和拥挤度来选择合适的个体组成新的父代种群。最后再通过选择、交叉,变异产生子代。重复。
还有几个主要的关键技术需要解释一下:
(1)快速非支配型排序
假设种群为P,则该算法需要计算P中的每个个体p的两个参数np和Sp,其中np为种群中支配个体p的个体数,Sp为种群中支配个体p的个体集合。遍历整个种群,这里那个两个参数的时间复杂度O(mN2)。
(2)拥挤度
在种群中给定点的周围个体密度,用id表示。它指出了在个体i周围包含个体i本身但不包含其他个体的最小的长方形。
(3)拥挤比较算子
经过快速非支配排序和拥挤度计算,种群中的每一个个体都得到了两个属性:非支配序rankn和拥挤度。利用这两个属性,我们可以区分种群中间任意两个个体间的支配和非支配关系。定义拥挤度比较算子,当且仅当irank>jrank或irank=jrank且id>jd,有个体i优于个体j。
(4)精英选择策略
精英策略是指在每一代的进化过程中,保留一部分优秀的个体,使得下一代的种群从父代和子代的合并种群中选择,从而提高算法的收敛性和解的质量。精英选择策略可以防止优秀的解被破坏或丢失,也可以加快非支配解集的收敛速度。
NSGAII中的精英选择策略具体如下:
- 在每一代,首先对父代种群进行交叉和变异操作,产生子代种群。
- 然后将父代种群和子代种群合并为一个大小为2N的种群,其中N是种群大小。
- 对合并种群进行快速非支配排序,根据Pareto支配关系将个体分成不同的层级,并给每个个体赋予一个等级值。
- 从最高层级开始,依次将每个层级的个体加入到下一代种群中,直到下一代种群达到N个个体或者超过N个个体。
- 如果最后一个加入的层级导致下一代种群超过N个个体,则对该层级的个体进行拥挤度计算和比较,根据拥挤度大小选择部分个体加入到下一代种群中,使得下一代种群恰好有N个个体。
- 重复上述步骤,直到达到预设的进化代数。
总结来说,相比于单目标函数求解,多目标函数求解明显难度提升了好几个数量级,其核心问题在于出现Pareto解。我们需要权衡各个目标函数之间的利弊,选择合适算法来求解。
下面是NSGA3算法流程图: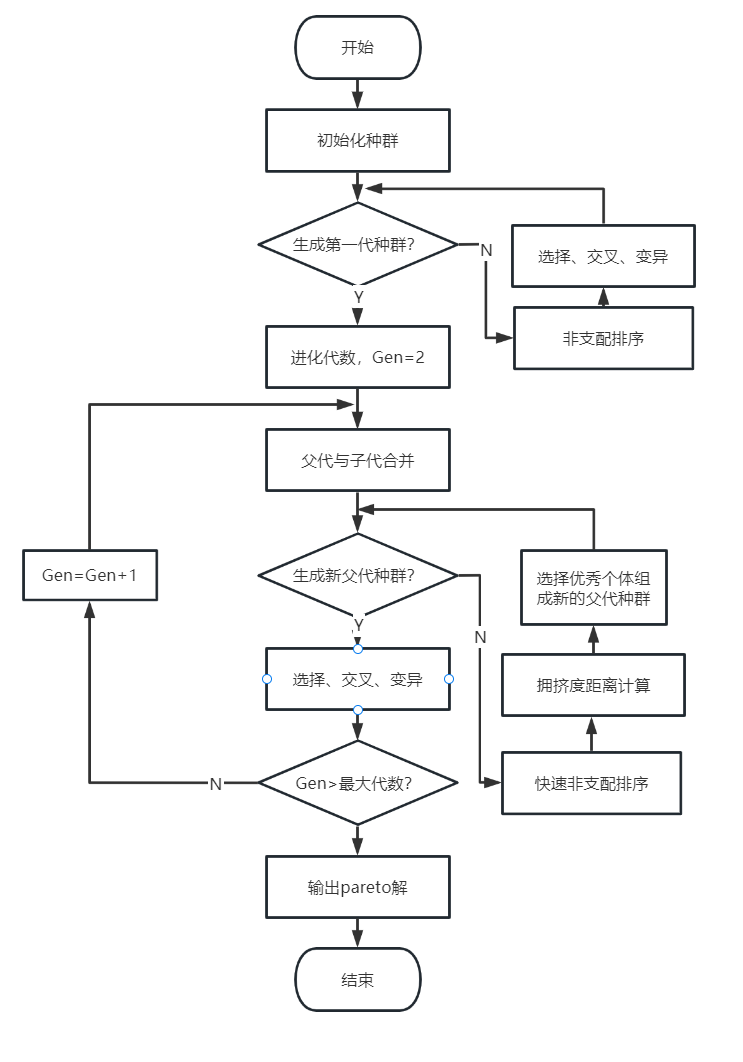
NSGA-III算法相比于NSGA和NSGA-II算法:
- NSGA-III算法引入了一组均匀分布的参考点,用于指导种群的选择,保持种群的多样性和收敛性。参考点的数量和位置可以根据目标个数和种群大小自适应地确定,而不需要人为地设定。
- NSGA-III算法采用了一种新的归一化方法,即用理想点和截距点将目标空间映射到单位超立方体中,然后计算每个个体与最近的参考点的距离,根据距离和参考点的拥挤度进行选择,这样可以避免目标之间的尺度差异和非均匀分布的影响。
- NSGA-III算法在选择过程中,不仅考虑了个体的非支配等级,还考虑了个体的参考点关联度,即个体与参考点的距离和参考点的拥挤度,这样可以更好地平衡种群的多样性和收敛性,同时也可以避免过度选择或忽略某些目标。
结论
多目标遗传算法的核心思想是,没有最好的解,只有最合适的解。所以,不要太担心你的选择是否正确,只要你能找到一个让你满意的解,就可以啦。
