当前位置： 首页 > article >正文

第二十六天-统计与机器学习SciPy，Scikit-Leaen

article 2024/12/24 20:13:04

目录

1.介绍

2.使用scipy

1. 安装

2.拟合曲线

3.随机变量与概率分布

4.假设检验

5.参数检验

3.使用Scikit-Learn

1. 机器学习库，建立在numpy,scipy,matplotlib基础上

2.包含功能

3.安装

1.官网：https://scikit-learn.org

2.下载

3.线性回归模型

4.归一化

5.标准化

6.OneHot独热编码

7.非监督学习-聚类算法K-Means

8.监督学习-KNN算法

9.监督学习-回归模型-多元线性回归模型

1.介绍

1.应用库基础关系

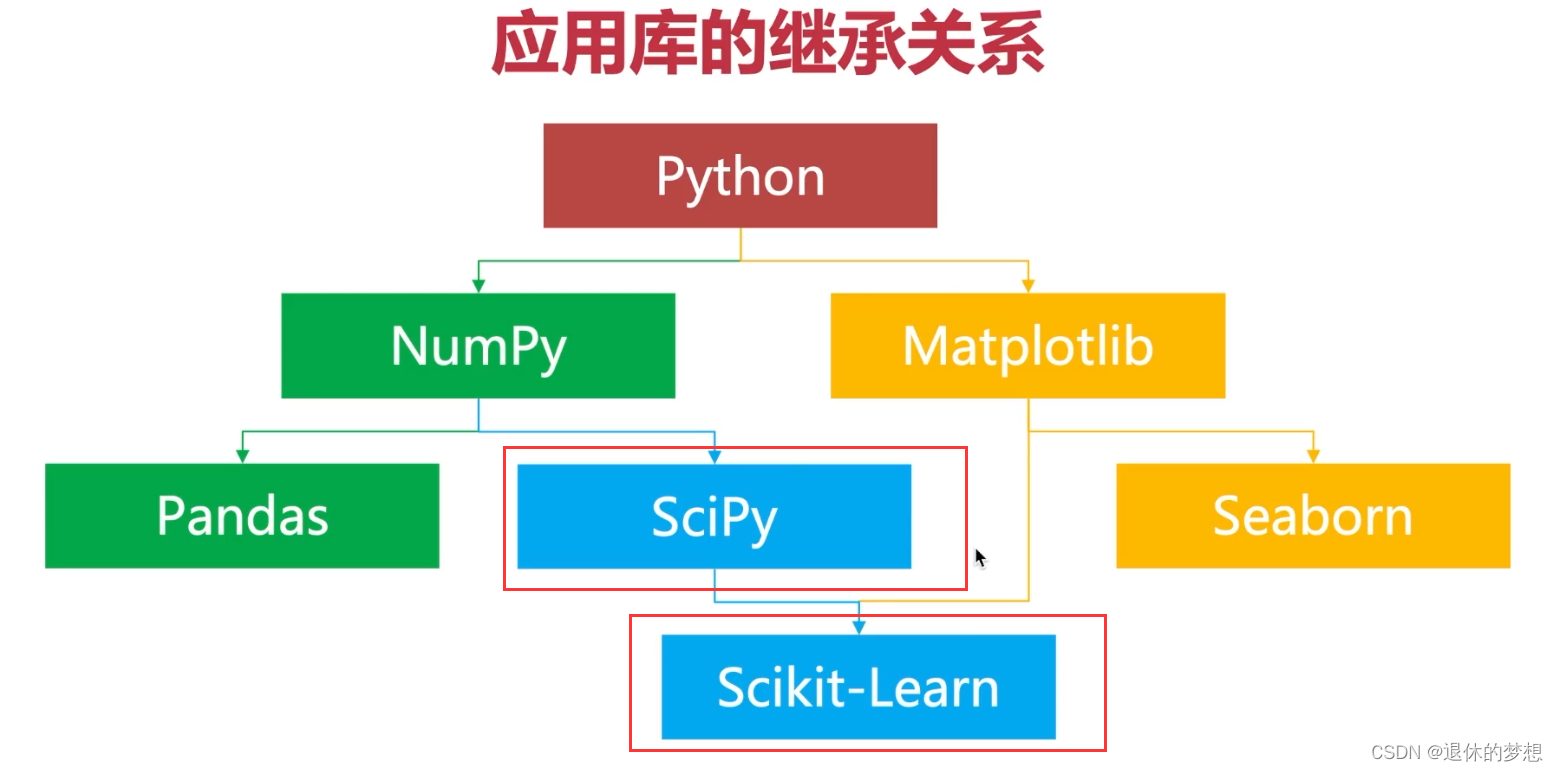
2..scipy是用于统计函数：如矩阵运算，参数优化，假设检验

3.Scikit-Learn回归算法：监督学习、分类算法、回归算法

4.Scikit-learn聚类算法：非监督学习，特征聚类分群

4.scipy官网：SciPy -

2.使用scipy

1. 安装

pip install scipy

import scipy

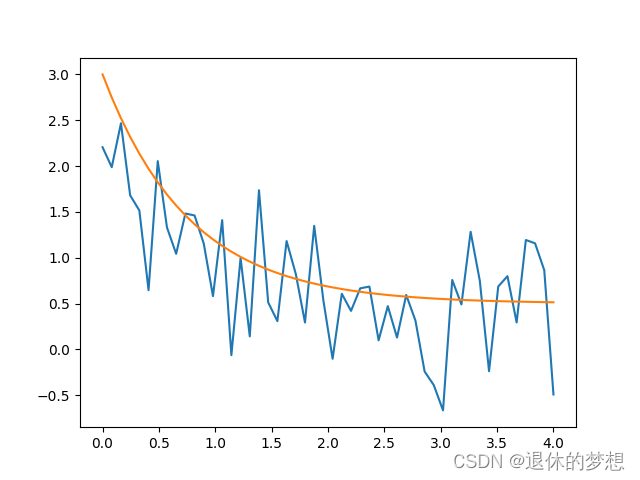
2.拟合曲线

# coding:utf-8

import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize


# 创建e方程= a*e^(-b*x)+c
def y(x, a, b, c):
    return a * np.exp(-b * x) + c


xdata = np.linspace(0, 4, 50)
ydata = y(xdata, 2.5, 1.3, 0.5)
ydata_noise = ydata + 0.5 * np.random.randn(xdata.size)
print(xdata)
print(ydata)

plt.plot(xdata, ydata_noise)
# 生成拟合曲线
params, pcov = scipy.optimize.curve_fit(y, xdata, ydata)
plt.plot(xdata,y(xdata,*params))

plt.show()

3.随机变量与概率分布

1. 统计学的应用价值

  • 应用数学的一个分支
  • 利用概率论建立数学模型，收集所2观察系统的数据
  • 进行量化分析，总结，进而进行推断和预测
  • 为相关决策提供依据和参考 

2.什么是随机变量

  • 观察数据样本：1.具有不确定性和随机性 2.落在某一个范围的概率是一定的

3.什么是概率分布

  • 随机变量取值的概率：某件事的概率，就是这件事在当前样本或者说实验中出现的次数，出现的可能性的意思

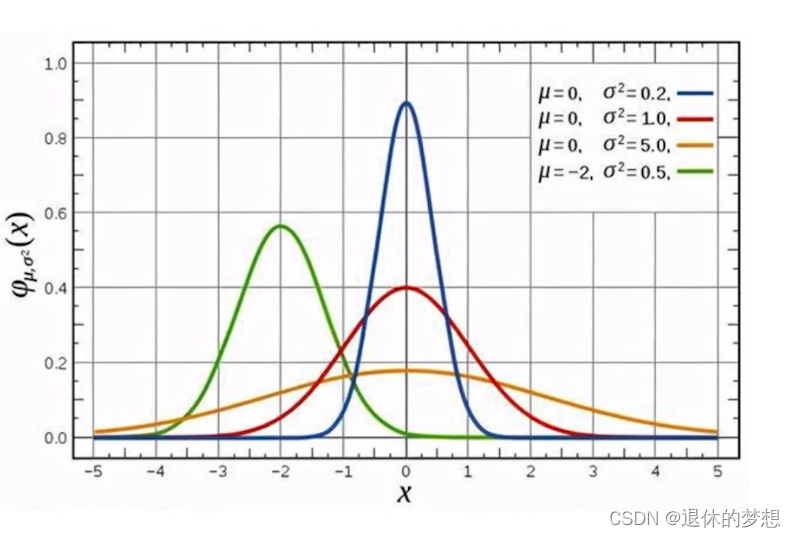
4.概率分布值正态分布：

  一般为中间高2边低成为正态分布，可以确立正常的取值范围

# coding:utf-8


import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
import seaborn as sns

#创建随机变量，设置size，设置loc期望值，设置scale方差
rvs1=st.norm.rvs(0,1,100)

#改的方差缓存变化
rvs2=st.norm.rvs(0,2,100)
rvs3=st.norm.rvs(0,3,100)

#绘制分布图
for i in [rvs1,rvs2,rvs3]:
    sns.distplot(i)
#设置lable
plt.legend(labels=["1","2","3"])

plt.show()

4.假设检验

1.什么是统计推断

  • 通过样本推断总体的一种统计方法
  • 通过概率分布的数量特征（如期望和方差）来反映22
  • 对总体的位置参数进行估计
  • 对于参数的假设进行检查
  • 对总体进行预测预报等

2.什么是假设检验

  • 判断样本与样本、样本与总体的差异
  • 是由”抽样误差”引起的还是“本质差别”照成的统计推断方法

如：

3.显著性检验

  • 通过对总体的特征，做出某种假设，并进行抽样研究的统计推理方法
  • 最终基于出现概率的大小，并判断接受或者拒绝某种假设

如：

# coding:utf-8


import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
import seaborn as sns
import matplotlib as mpl

mpl.rcParams["font.family"] = "FangSong"  # 设置字体
mpl.rcParams["axes.unicode_minus"] = False  # 正常显示负号

#设置样本的概率分布
#整体样本
mean0=72
#有效样本数量
mean1=68
#方差0.8
std1=0.8
rvs0=st.norm.rvs(mean0,1,1000)
rvs1=st.norm.rvs(mean1,std1,1000)

for i in [rvs0,rvs1]:
    sns.distplot(i)

#置信区间：总体概率为95%


#设置lable
plt.legend(labels=["72样本","68样本"])

plt.show()

5.参数检验

1.置信区间：总体概率为95%

2.样本差异性比较：stats.ks_2samp(样本1,样本2,"类型")

3.使用Scikit-Learn

1. 机器学习库，建立在numpy,scipy,matplotlib基础上

2.包含功能

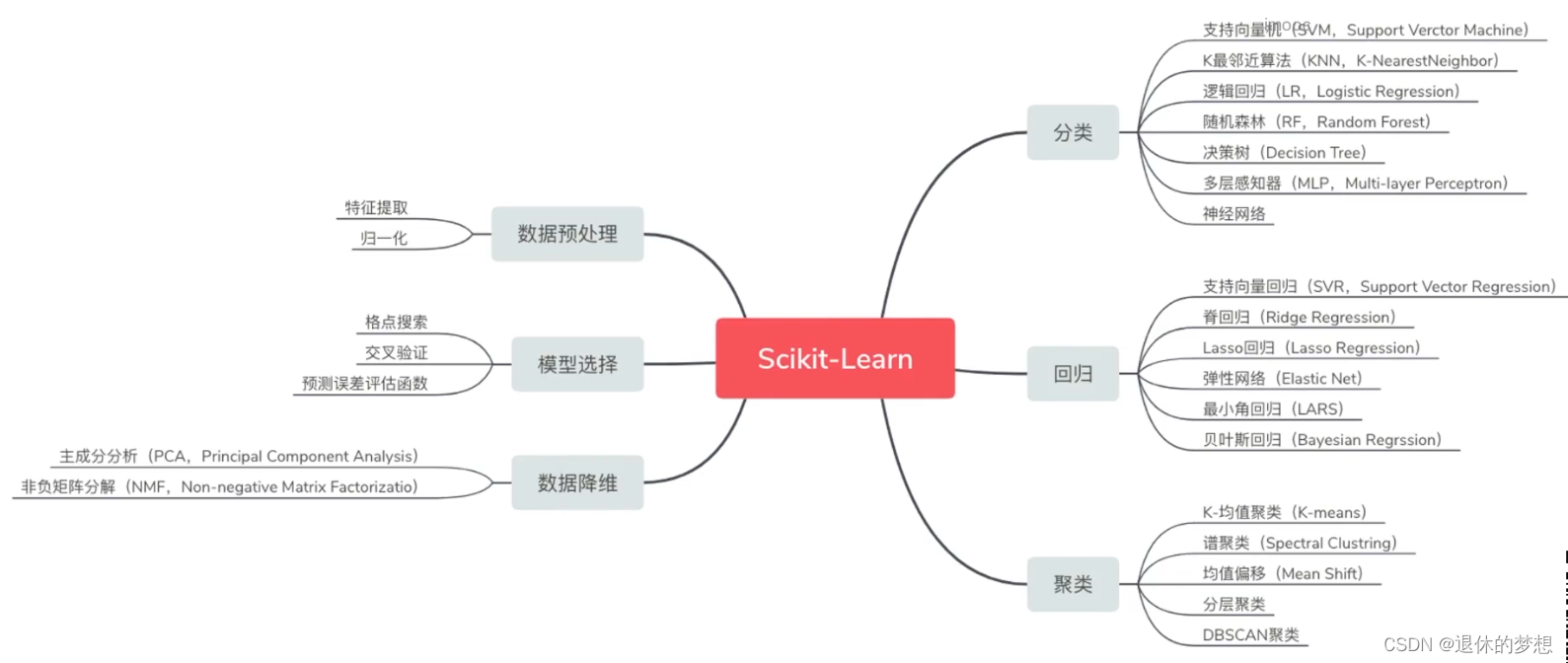
3.安装

1.官网：https://scikit-learn.org

2.下载

pip install scikit-learn

3.线性回归模型

# coding:utf-8

import pandas as pd
import numpy as np
import sklearn as sk
from sklearn import datasets
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 导入波士顿房价数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep=r"\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
# 人口中地位较低的百分比
target = raw_df.values[1::2, 2]
# print("data=====",data)
print("target======", target)
# 样本数据
# print(data.shape)


house = pd.DataFrame(data)
house.columns = ["城市的人均犯罪率", " 25,000英尺以上的住房占的比例", "每个城镇的非零售商业英亩的比例", "如果靠近河岸",
                 "环保指数", "每个住宅的平均房间数", "自住比例", "就业中心距离",
                 "到公路的可达指数", "物业税", "学生教师比例", "黑人比例", "人口中地位较低的百分比"]
print(house)
# 使用回归线性模型 y=w*x +b

mod = LinearRegression()  # 确定要调用的模型
x = data[:, np.newaxis, 5]  # 房间数
y = target  #
mod.fit(x, y)
# 相关性指数 0-1
print("相关性指数：", mod.score(x, y))
print("回归系数coef_：", mod.coef_)
print("回归系数intercept_：", mod.intercept_)

# 绘制样本
plt.scatter(x, y)
plt.plot(x, mod.predict(x), color="red")

plt.show()

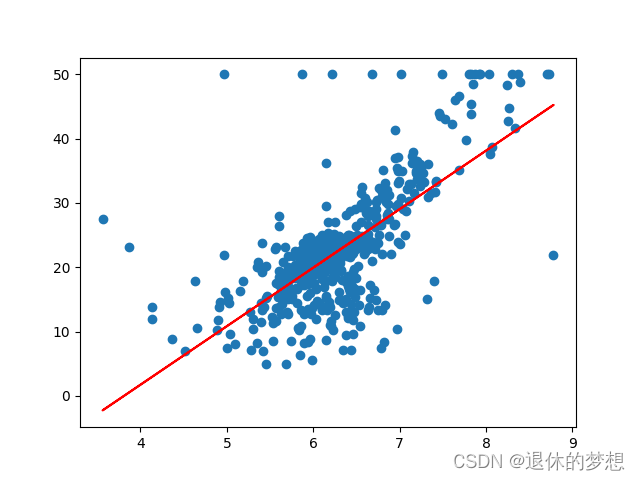
4.归一化

1.数据归一化的作用是为了降低数据差异，将数据的取值范围设置在0-1

# coding:utf-8

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mpl
import sklearn as sk
import matplotlib.pyplot as plt
from sklearn import preprocessing as prep

mpl.rcParams["font.family"] = "FangSong"  # 设置字体
mpl.rcParams["axes.unicode_minus"] = False  # 正常显示负号

fig, ax = plt.subplots(2, 2)
# 创建随机样本
data = pd.DataFrame({
    "a": np.random.exponential(3, 1000),  # a数据为 3的方差，生成1000个数字
    "b": np.random.normal(-5, 0.5, 1000),  # b数据为以-5位中心，0.5的方差，生成1000个数字
    "c": np.random.normal(0, 4, 1000)  # 以0位为中心，4的方差，生成1000个数字
})
print("数据样本:", data.describe())
# 原始数据 则线图
sns.lineplot(data, ax=ax[0, 0])
ax[0, 0].set_title("原始数据-折线图")

# 分布图
sns.distplot(data["a"], ax=ax[0, 1])
sns.distplot(data["b"], ax=ax[0, 1])
sns.distplot(data["c"], ax=ax[0, 1])
ax[0, 1].set_title("原始数据-分布图")

# 数据归一化的作用是为了降低数据差异，将数据的取值范围设置在0-1
# 归一化模型 算法：X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
scaler1 = prep.MinMaxScaler()
scaler1.fit(data)

minMax1 = pd.DataFrame(scaler1.transform(data), columns=["a", "b", "c"])

sns.lineplot(data=minMax1, ax=ax[1, 0])
ax[1, 0].set_title("归一化-折线图")

sns.distplot(minMax1["a"], ax=ax[1, 1])
sns.distplot(minMax1["b"], ax=ax[1, 1])
sns.distplot(minMax1["c"], ax=ax[1, 1])
ax[1, 1].set_title("归一化-分布图")

# 设置间距,避免名称重叠
fig.tight_layout()

plt.show()

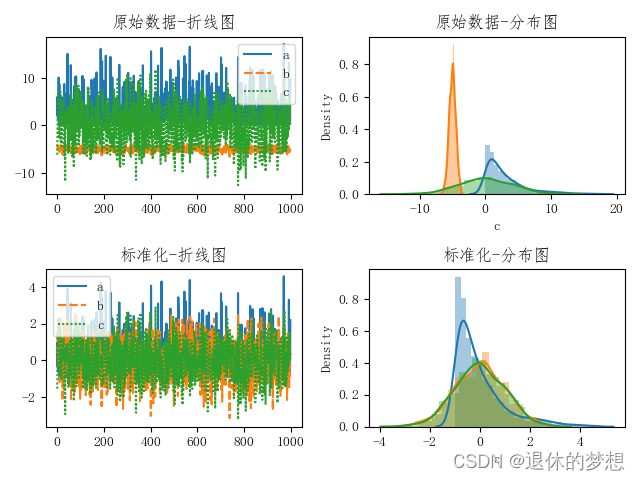
5.标准化

 数据标准化， 将数据转换为0为均值，1位方差
# coding:utf-8

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mpl
import sklearn as sk
import matplotlib.pyplot as plt
from sklearn import preprocessing as prep

mpl.rcParams["font.family"] = "FangSong"  # 设置字体
mpl.rcParams["axes.unicode_minus"] = False  # 正常显示负号

fig, ax = plt.subplots(2, 2)
# 创建随机样本
data = pd.DataFrame({
    "a": np.random.exponential(3, 1000),  # a数据为 3的方差，生成1000个数字
    "b": np.random.normal(-5, 0.5, 1000),  # b数据为以-5位中心，0.5的方差，生成1000个数字
    "c": np.random.normal(0, 4, 1000)  # 以0位为中心，4的方差，生成1000个数字
})
print("数据样本:", data.describe())
# 原始数据 则线图
sns.lineplot(data, ax=ax[0, 0])
ax[0, 0].set_title("原始数据-折线图")

# 分布图
sns.distplot(data["a"], ax=ax[0, 1])
sns.distplot(data["b"], ax=ax[0, 1])
sns.distplot(data["c"], ax=ax[0, 1])
ax[0, 1].set_title("原始数据-分布图")

# 数据标准化， 将数据转换为0为均值，1位方差
scaler1 = prep.StandardScaler()
scaler1.fit(data)

minMax1 = pd.DataFrame(scaler1.transform(data), columns=["a", "b", "c"])

sns.lineplot(data=minMax1, ax=ax[1, 0])
ax[1, 0].set_title("标准化-折线图")

sns.distplot(minMax1["a"], ax=ax[1, 1])
sns.distplot(minMax1["b"], ax=ax[1, 1])
sns.distplot(minMax1["c"], ax=ax[1, 1])
ax[1, 1].set_title("标准化-分布图")

# 设置间距,避免名称重叠
fig.tight_layout()

plt.show()

6.OneHot独热编码

1. 自然编码vs独热编码

独热编码是以0和1表示的，将特定类特征的转换为二进制

比如：性别：男、女 以编码标识为 1,0  独热编码为 男：[1,0] 女[0,1]

再比如：胜平负 1胜利 2平 3负 独热编码为 胜：[1,0,0] 平：[0,1,0]  负：[0,0,1]

from sklearn import preprocessing as prep
import pandas as pd

sex = ["f", "m"]
spf = ["s", "p"]
zhiffs = ["x", "z"]

df = pd.DataFrame([sex,spf,zhiffs])
# 创建模型》fit训练数据》transform显示数据》.attribute打印数据
oneHot = prep.OneHotEncoder(sparse_output=False,handle_unknown='ignore')
oneHot.fit(df)
print(oneHot.transform([["f","m"]]))

out:

[[1. 0. 0. 1. 0. 0.]]

7.非监督学习-聚类算法K-Means

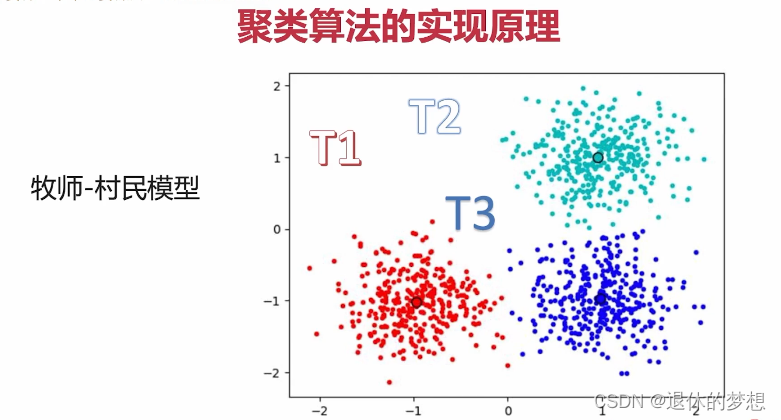
8.监督学习-KNN算法

9.监督学习-回归模型-多元线性回归模型


http://www.kler.cn/a/274227.html

相关文章：

  • 再服务器上建立新的编译环境
  • 利用Gurobi追溯模型不可行原因的四种方案及详细案例
  • 递归读取指定目录下的文件
  • PromptGIP：Unifying lmage Processing as Visual Prompting Question Answering
  • Linux中Mysql5.7主从架构(一主多从)配置教程
  • JVM对象分配内存如何保证线程安全？
  • Laravel Class ‘Facade\Ignition\IgnitionServiceProvider‘ not found 解决
  • docker-compose Install 容器化Windows 系统
  • Java 文件处理完全指南：创建、读取、写入和删除文件详细解析
  • BSD-3-Clause是一种开源软件许可协议
  • git是什么git能做什么
  • 腾讯春招后端一面（算法篇）
  • LlamaParse: 高效的PDF文件RAG解析工具
  • Java——网络编程
  • 论文阅读——Vision Transformer with Deformable Attention
  • Leetcode 387. First Unique Character in a String
  • 【研发日记】Matlab/Simulink技能解锁(五)——Simulink布线技巧
  • 在sql server 2016 always on集群里新增一个数据库节点
  • 【数据结构】链表力扣刷题详解
  • Flutter 初始WidgetState 简单应用案例分析
  • LAMP架构部署--yum安装方式
  • 微信小程序小白易入门基础教程1
  • pytorch DDP模式下, 获取数据的的preftech + stream
  • 【SVG】前端-不依靠第三方包怎么画连线???
  • 装X神器，装X图片生成器，高富帅模拟器
  • 安卓基础面试题