图论----最小生成树讲解与相关题解

目前已更新系列

当前--图论----最小生成树讲解与相关题解

滑动窗口系列算法总结与题解一

算法系列----并查集总结于相关题解

图论---dfs系列

差分与前缀和总结与对应题解（之前笔试真的很爱考）

数论---质数判断、质因子分解、质数筛（埃氏筛、
 

最小生成树

是什么、有什么用

最小生成树：在无向带权图中选择一些边，在保证连通性的情况下，边的总权值最小

最小生成树可能不止一颗，只要保证边的权值最小，那就是最小生成树

如果无向带权图有n个点那么最小生成树一定会有n-1条边

扩展：最小生成树一定是最小瓶颈树

解决该类问题最好用的方法时KrusKal算法

• 不需要建图，只用使用并查集的思想将建立一个father数组表示当前节点是属于哪个集合
• 然后将边按照权值进行排序，遍历排序后的边，尝试将边上的点进行合并
• 遍历完之后如果能够合并的边数==n-1条说明找到了一条最小生成树，没有找到说明该图不连通

一般遇到题目将你求将n个点联通然后求联通之后的每条边的权值最小，

或者求最小瓶颈树，也就是让每个点联通，保证总体权值最小，求在最小瓶颈树上边的最大权值，

Kruskal算法（最常用）

思路

• 1、把所有的边从小到大进行排序，从权值小的边开始考虑（可以使用最小堆，也可以调用sort进行排序）
• 2、如果连接当前的边不会形成环，就选择当前的边
• 3、如果当前的边会形成环，就不要当前的边
• 4、考察完所有边之后，最小生成树就得到了（或者得到n-1条边之后）

模板

题目链接：【模板】最小生成树 - 洛谷

最小生成树主要是用来求将找出图中所有

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.PriorityQueue;

/**
 * @Author wangdongsheng
 * @Date 2024/8/19 00:18
 */
public class Main {
    //建图所用
    public static final int MAXN=5010;
    public static final int MAXM=2*MAXN;



    //并查集所用
    static int[] father=new int[MAXN];
    //kuraskal算法所用
    //0:from,1:to,2:weight
    static PriorityQueue<int[]> heap=new PriorityQueue<>((a,b)->a[2]-b[2]);
    //并查集所用
    private static void build(int n){
        for (int i = 0; i <=n; i++) {

            father[i]=i;
        }
    }
    public static int find(int x){
        if (father[x]!=x){
            father[x]=find(father[x]);
        }
        return father[x];
    }
    //这里合并返回是否是同一个集合是为了如果能合并说明不是环那么计算权制
    //如果是false那么可能出现环不能计算权制
    public static boolean union(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if (fx!=fy){
            father[fx]=fy;
            return true;
        }
        return false;

    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        in.nextToken();int n=(int) in.nval;
        in.nextToken();int m=(int) in.nval;
        build(n);
        for (int i = 0; i < m; i++) {
            in.nextToken();int u=(int) in.nval;
            in.nextToken();int v=(int) in.nval;
            in.nextToken();int w=(int) in.nval;
            //放入小根队中，将边进行排序
            heap.offer(new int[]{u,v,w});
        }
        int cnt=0;//记录小根队中弹出的边数用来判断是否有环
        int ans=0;
        while (!heap.isEmpty()){
            int[] poll = heap.poll();
            int u=poll[0];
            int v=poll[1];
            int w=poll[2];
            if (union(u,v)){
                cnt++;
                ans+=w;

            }

        }
        System.out.println(cnt==n-1?ans:"orz");
    }

}

下面是使用sort进行排序的模板

public class 最小生成树 {
    public static int MAXN=5001;
    public static int MAXM=200001;
    public static int[] father=new int[MAXN];
    public static int[][] eages=new int[MAXM][3];
    public static void build(int m){
        for (int i = 1; i <=m ; i++) {
            father[i]=i;
        }
    }
    public static int find(int a){
        if(a!=father[a]){
            father[a]=find(father[a]);
        }
        return father[a];
    }
    public static boolean union(int a,int b){
        int fa=find(a);
        int fb=find(b);
        if (fa!=fb){
            //如果两个点代表的集合不是同一个，合并
            father[fa]=fb;
            return true;
        }else {
            return false;
            //说明两个点在同一个集合中，则说明要这条边就会形成环，返回false
        }
    }

    public static void main(String[] args) {
        int n,m;
        Scanner scanner = new Scanner(System.in);
        n=scanner.nextInt();
        m=scanner.nextInt();
        for (int i = 0; i < m; i++) {
            eages[i][0] = scanner.nextInt();
            eages[i][1] =scanner.nextInt();
            eages[i][2]=scanner.nextInt();
        }
        int ans=0;
        int eageCount=0;//记录合并使用了几条边，用于判断是否联通

        //排序
        Arrays.sort(eages,(a,b)->a[2]-b[2]);//以权值进行排序

        //开始并查集
        //初始化father数组
        build(n);
        for (int[] eage : eages) {
            if (union(eage[0],eage[1])){
                //合并
                eageCount++;
                ans+=eage[2];//加上权值
            }
            //出现环就不要这条边
        }
        System.out.println(eageCount==n-1?ans:"orz");
    }
}

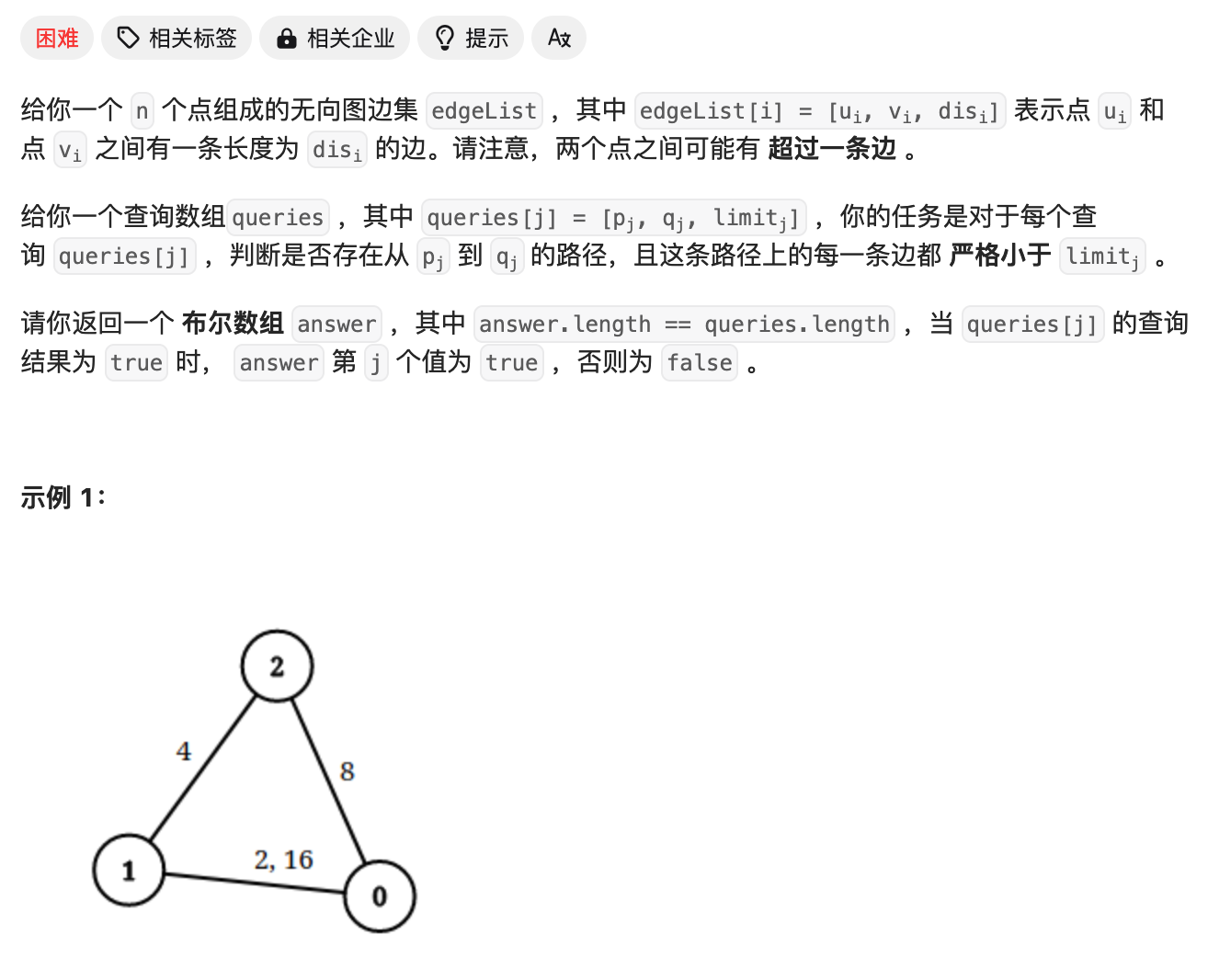
检查边长度限制的路径是否存在

题目描述

解析

这题主要是理解题目：题目的意思就是给你一个请求查询数组queries，然后queries[i][0]表示from,queries[i][1]表示to，queries[i][2]:表示权制，题目就是要找出有没有一条从from到to的路径，使得每一条表的权制不超过限制的权制，

class Solution {

    //这题要求的是，给定一个查询，查询，u,v,w表示u到v的每一条边必须要小于限制w
    //所以我们转化一下思维，我们通过最小生成树的思想，同样先合并最小权制的边，
    //然后，将边权制小于限制的进行合并，
    //最后查询的时候就直接判断是否在同一个集合中就好了
    //然后有几个查询我们就做几次最小生成树
    //然后优化一下，我们可以让查询的边安权制排序后进行找答案，
    //由于要排序，排序之后原来数组的顺序就改变了，
    //因此我们数组中还需要记录对应原始的下标，这样就能复用并查集了
    //这是个无向图
    public static int MAXN = 100010;
    public static final int MAXM = 2 * MAXN;
    public static int[] father = new int[MAXN];

    //并查集
    public static void build(int n) {
        for (int i = 0; i <= n; i++) {
            father[i] = i;
        }
    }

    public static int find(int x) {
        if (father[x] != x) {
            father[x] = find(father[x]);
        }
        return father[x];
    }

    public static void union(int x, int y) {
        int fx = find(x);
        int fy = find(y);
        if (fx != fy) {
            father[fx] = fy;
        }
    }

    public static boolean isSame(int x, int y) {
        return find(x) == find(y);
    }

    public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
        build(n);
        //拷贝查询数组，添加一个索引
        //0:索引，1:索引，2:v，3:w
        int[][] newQueries = new int[queries.length][4];
        for (int i = 0; i < queries.length; i++) {
            newQueries[i][0] = i;
            newQueries[i][1] = queries[i][0];
            newQueries[i][2] = queries[i][1];
            newQueries[i][3] = queries[i][2];
        }
        //
        // 将这个按照权制排序减少重复建立最小生成树
        Arrays.sort(newQueries, (a, b) -> a[3] - b[3]);
        //将给的边进行排序
        Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);
        boolean[] ans = new boolean[queries.length];
        //注意i放在外层，因为我们已经对查询的权制进行了排序，那么建立的并查集就是可以复用的
        int i = 0;
        for (int[] query : newQueries) {
            int rw = query[3];
            int ru = query[1];
            int rv = query[2];
            int index = query[0];
            //并查集
            for (; i < edgeList.length && (edgeList[i][2] < rw); i++) {
                int u = edgeList[i][0];
                int v = edgeList[i][1];
                union(u, v);

            }
            if (isSame(ru, rv)) {
                ans[index] = true;
            }
        }
        return ans;

    }
}

繁忙的都市

题目链接：[SCOI2005] 繁忙的都市 - 洛谷

题目描述

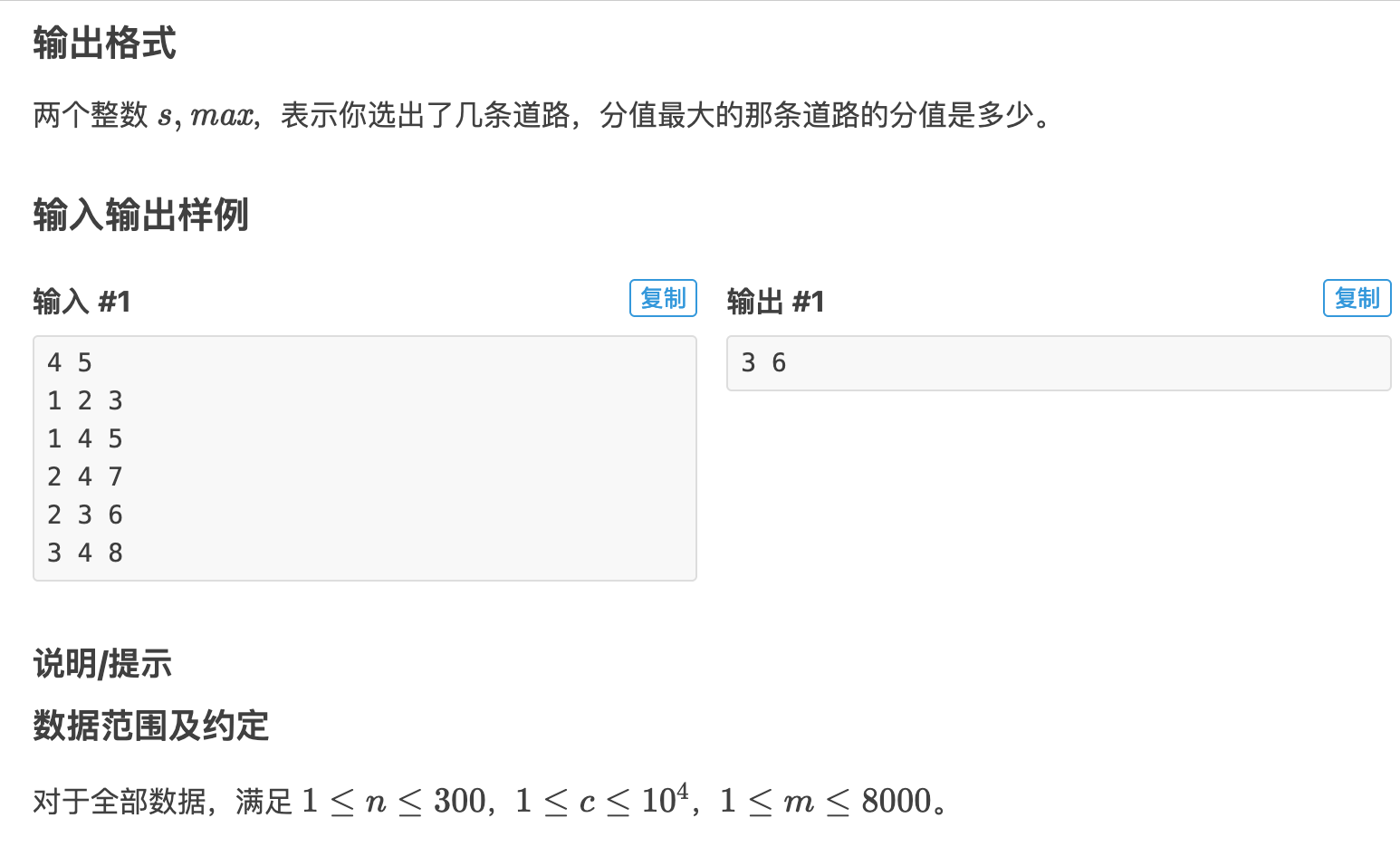
解析

这题也是模板题直接套模板就好了

public class Main {

    public static int MAXN=310;
    private static int MAXM=2*8010;

    //这里直接试用最小堆进行排序算了，就不用再去存放边的信息，然后再对边进行排序了
    private static PriorityQueue<int[]> minHeap=new PriorityQueue<>((a,b)->a[2]-b[2]);

    //并查集所用
    //记录并查中有多少条边，每次合并一次，边数就+1
    static int cnt=0;
    private static int[] father=new int[MAXN];
    private static void build(int n){
        for (int i = 0; i <=n; i++) {
            father[i]=i;
        }
        cnt=0;
    }
    private static int find(int x){
        if (father[x]!=x){
            father[x]=find(father[x]);
        }
        return father[x];
    }
    private static void union(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if (fx!=fy){
            father[fx]=fy;
            cnt++;
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        in.nextToken();int n=(int)in.nval;
        in.nextToken();int m=(int)in.nval;
        build(n);
        for (int i = 0; i < m; i++) {
            in.nextToken();int u=(int)in.nval;
            in.nextToken();int v=(int)in.nval;
            in.nextToken();int w=(int)in.nval;
            minHeap.offer(new int[]{u,v,w});
//            minHeap.offer(new int[]{v,u,w});
        }

        //Kruskal
        int max=0;

        while (!minHeap.isEmpty()){
            int[] poll = minHeap.poll();
            max=poll[2];
            union(poll[0],poll[1]);
            if (cnt==n-1) break;
        }
        System.out.println(cnt+" "+max);
    }
}