自制深度学习推理框架之卷积和池化算子的设计与实现
文章目录
- 一、池化算子
- 1.1 池化定义
- 1.2 maxpooling实现
- 1.2 1 Forward前向计算
- 1.2.2 GetInstance实例化Layer
- 1.2.3 LayerRegistererWrapper注册算子
- 二、卷积算子
- 2.1 卷积定义
- 2.2 Im2col优化卷积计算
- 2.3 分组卷积
- 2.4 Im2Col实现
- 2.5 卷积算子实现
- 2.5.1 GEMM实现
- 2.5.2 卷积算子的实例化
一、池化算子
1.1 池化定义
池化算子是神经网络中的一种常见操作,主要用于减少特征图的尺寸,同时保持其重要的特征信息。池化层通常位于卷积层之后,其作用是减少卷积层输出的尺寸,使模型更容易处理高维数据,同时减小计算量。池化算子通常有两种主要形式:**最大池化(Max Pooling)**和平均池化(Average Pooling)。
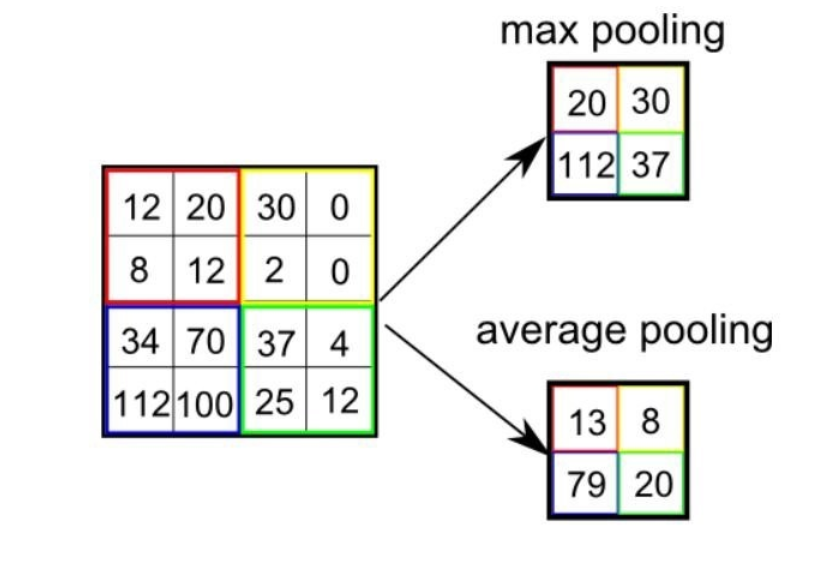
池化算子会在固定形状的窗口(即池化窗口)内对输入数据的元素进行计算,计算结果可以是池化窗口内元素的最大值或平均值,以上图为例,相同颜色区域表示一个2 x 2的池化窗口。在二维最大池化中,池化窗口从输入张量的左上角开始,按照从左往右、从上往下的顺序依次滑动(滑动的幅度称为stride=2)。在每个池化窗口内,取窗口中的最大值或平均值作为输出张量相应位置的元素。
每次进行池化操作时,池化窗口都按照从左到右、从上到下的顺序进行滑动。窗口每次向下移动的步长为stride height,向右移动的步长为stride width。池化操作的元素数量由pooling height和pooling width所组成的池化窗口决定。
池化操作后特征图的大小可以根据以下公式计算:假设输入特征图的大小为 H in × W in H_{\text{in}} \times W_{\text{in}} Hin×Win ,池化窗口的大小为 K h × K w K_h \times K_w Kh×Kw ,步幅(Stride)为 S h × S w S_h \times S_w Sh×Sw ,填充(Padding)为 P h × P w P_h \times P_w Ph×Pw ,则输出特征图的大小为 H out × W out H_{\text{out}} \times W_{\text{out}} Hout×Wout。
- 输出特征图的高度 H out H_{\text{out}} Hout :
H out = ⌊ H in + 2 P h − K h S h ⌋ + 1 H_{\text{out}} = \left\lfloor \frac{H_{\text{in}} + 2P_h - K_h}{S_h} \right\rfloor + 1 Hout=⌊ShHin+2Ph−Kh⌋+1
- 输出特征图的宽度 W out W_{\text{out}} Wout :
W out = ⌊ W in + 2 P w − K w S w ⌋ + 1 W_{\text{out}} = \left\lfloor \frac{W_{\text{in}} + 2P_w - K_w}{S_w} \right\rfloor + 1 Wout=⌊SwWin+2Pw−Kw⌋+1
如果使用填充,输入特征图的边缘会在池化前被填充指定数量的像素,以控制输出特征图的大小。这对于确保输入特征图大小和输出特征图大小满足某些需求(如特定的下采样率)非常有用。
对于多通道的池化算子和单通道上的池化算子实现方式基本相同,池化操作会分别应用于每个通道,每个通道的池化操作是独立的,池化窗口在每个通道内滑动,并生成相应的输出。池化不改变输入特征图的维度,只改变特征图的大小!
1.2 maxpooling实现
最大池化指的是在一个窗口的范围内,取所有元素的最大值
// MaxPoolingLayer 类表示一个最大池化层,继承自 NonParamLayer。
class MaxPoolingLayer : public NonParamLayer {
public:
// 初始化最大池化层的参数。
explicit MaxPoolingLayer(uint32_t padding_h, uint32_t padding_w,
uint32_t pooling_size_h, uint32_t pooling_size_w,
uint32_t stride_h, uint32_t stride_w);
// 前向传播函数,用于执行最大池化操作。
// - inputs: 输入特征图的张量列表,每个张量表示一个输入通道。
// - outputs: 输出特征图的张量列表,每个张量表示一个输出通道。
InferStatus Forward(
const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
std::vector<std::shared_ptr<Tensor<float>>>& outputs) override;
// 静态方法,用于从 RuntimeOperator 实例化 MaxPoolingLayer 对象。
// - op: 包含层参数的 RuntimeOperator 对象。
// - max_layer: 输出的最大池化层对象指针。
static ParseParameterAttrStatus GetInstance(
const std::shared_ptr<RuntimeOperator>& op,
std::shared_ptr<Layer>& max_layer);
private:
uint32_t padding_h_ = 0; // 高度方向的填充大小,默认值为0
uint32_t padding_w_ = 0; // 宽度方向的填充大小,默认值为0
uint32_t pooling_size_h_ = 0; // 池化窗口的高度,默认值为0
uint32_t pooling_size_w_ = 0; // 池化窗口的宽度,默认值为0
uint32_t stride_h_ = 1; // 高度方向的步幅,默认值为1
uint32_t stride_w_ = 1; // 宽度方向的步幅,默认值为1
};
最大池化层用于降低特征图的分辨率,通过选取池化窗口内的最大值进行下采样。MaxPoolingLayer类这是一个表示最大池化操作的类。最大池化是卷积神经网络中常用的操作,用于下采样特征图。
1.2 1 Forward前向计算
Forward函数执行最大池化操作,输入和输出均为张量列表,每个张量表示一个通道的特征图。方法负责在输入特征图上应用最大池化操作,并将结果存储在输出张量中。
所有算子都会派生于Layer父类并重写其中带参数的Forward方法,子类的Forward方法会包含派生类算子的具体计算过程:
- 从输入数组中提取每个输入张量,并对其进行空值和维度检查,以确保数据有效性。
- 根据算子的定义和输入张量的值,执行特定的计算逻辑。
- 将计算结果写回到输出张量中,从而完成算子的计算过程。
InferStatus MaxPoolingLayer::Forward(
const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
std::vector<std::shared_ptr<Tensor<float>>>& outputs) {
// 检查输入张量是否为空
if (inputs.empty()) {
LOG(ERROR) << "The input tensor array in the max pooling layer is empty";
return InferStatus::kInferFailedInputEmpty;
}
// 检查输入和输出张量的数量是否匹配
if (inputs.size() != outputs.size()) {
LOG(ERROR)
<< "The input and output tensor array size of the max pooling layer "
"do not match";
return InferStatus::kInferFailedInputOutSizeMatchError;
}
const uint32_t batch = inputs.size(); // 批处理的大小,即输入张量的数量
const uint32_t pooling_h = pooling_size_h_; // 池化窗口的高度
const uint32_t pooling_w = pooling_size_w_; // 池化窗口的宽度
// 检查步幅参数是否有效(步幅不能为0)
if (!stride_h_ || !stride_w_) {
LOG(ERROR) << "The stride parameter is set incorrectly. It must always be "
"greater than 0";
return InferStatus::kInferFailedStrideParameterError;
}
.......
// 对每个输入张量执行最大池化操作
for (uint32_t i = 0; i < batch; ++i) {
const std::shared_ptr<Tensor<float>>& input_data = inputs.at(i);
// 确保输入张量非空
CHECK(input_data == nullptr || !input_data->empty())
<< "The input tensor array in the max pooling layer has an "
"empty tensor "
<< i << "th";
const uint32_t input_h = input_data->rows(); // 输入张量的高度
const uint32_t input_w = input_data->cols(); // 输入张量的宽度
const uint32_t input_padded_h = input_data->rows() + 2 * padding_h_; // 填充后的输入高度
const uint32_t input_padded_w = input_data->cols() + 2 * padding_w_; // 填充后的输入宽度
const uint32_t input_c = input_data->channels(); // 输入张量的通道数
// 计算输出张量的高度和宽度
const uint32_t output_h = uint32_t(
std::floor((int(input_padded_h) - int(pooling_h)) / stride_h_ + 1));
const uint32_t output_w = uint32_t(
std::floor((int(input_padded_w) - int(pooling_w)) / stride_w_ + 1));
std::shared_ptr<Tensor<float>> output_data = outputs.at(i);
// 如果输出张量为空或未分配,则创建新张量
if (output_data == nullptr || output_data->empty()) {
output_data =
std::make_shared<Tensor<float>>(input_c, output_h, output_w);
outputs.at(i) = output_data;
}
// 检查输出张量的尺寸是否正确
CHECK(output_data->rows() == output_h && output_data->cols() == output_w &&
output_data->channels() == input_c)
<< "The output tensor array in the max pooling layer "
"has an incorrectly sized tensor "
<< i << "th";
// 对每个通道进行最大池化
for (uint32_t ic = 0; ic < input_c; ++ic) {
const arma::fmat& input_channel = input_data->slice(ic); // 获取输入通道
arma::fmat& output_channel = output_data->slice(ic); // 获取输出通道
// 遍历每个池化窗口的位置
for (uint32_t c = 0; c < input_padded_w - pooling_w + 1; c += stride_w_) {
int output_col = int(c / stride_w_); // 计算输出列索引
for (uint32_t r = 0; r < input_padded_h - pooling_h + 1;
r += stride_h_) {
int output_row = int(r / stride_h_); // 计算输出行索引
float* output_channel_ptr = output_channel.colptr(output_col); // 获取输出通道列指针
float max_value = std::numeric_limits<float>::lowest(); // 初始化最大值为最小可能的浮点数
// 在池化窗口内寻找最大值
for (uint32_t w = 0; w < pooling_w; ++w) {
const float* col_ptr = input_channel.colptr(c + w - padding_w_);
for (uint32_t h = 0; h < pooling_h; ++h) {
float current_value = 0.f;
// 检查当前元素是否在有效的输入范围内
if ((h + r >= padding_h_ && w + c >= padding_w_) &&
(h + r < input_h + padding_h_ &&
w + c < input_w + padding_w_)) {
current_value = *(col_ptr + r + h - padding_h_);
} else {
current_value = std::numeric_limits<float>::lowest(); // 如果不在范围内,赋最小值
}
max_value = max_value > current_value ? max_value : current_value; // 更新最大值
}
}
*(output_channel_ptr + output_row) = max_value; // 将最大值写入输出
}
}
}
}
return InferStatus::kInferSuccess; // 返回成功状态
}
首先检查输入张量是否为空,以及输入和输出张量的数量是否匹配。如果不满足这些条件,函数会返回错误状态。
将输入和输出的张量个数记作batch , 也就是一个批次处理的数据数量。通过输入张量的高度和宽度以及池化窗口、填充、步幅等参数,计算输出张量的高度和宽度。如果计算出的尺寸无效(宽度或高度为0),函数会返回错误。
完成上面两个步骤后,接下来就可以进行池化操作。对每个输入通道,即batch size个输入张量进行遍历处理,根据前面的计算公式获得该输出张量的高度和宽度,然后就对每个通道进行最大池化。
// 对每个通道进行最大池化
for (uint32_t ic = 0; ic < input_c; ++ic) {
const arma::fmat& input_channel = input_data->slice(ic); // 获取输入通道
arma::fmat& output_channel = output_data->slice(ic); // 获取输出通道
// 遍历每个池化窗口的位置
for (uint32_t c = 0; c < input_padded_w - pooling_w + 1; c += stride_w_) {
int output_col = int(c / stride_w_); // 计算输出列索引
for (uint32_t r = 0; r < input_padded_h - pooling_h + 1;
r += stride_h_) {
int output_row = int(r / stride_h_); // 计算输出行索引
float* output_channel_ptr = output_channel.colptr(output_col); // 获取输出通道列指针
float max_value = std::numeric_limits<float>::lowest(); // 初始化最大值为最小可能的浮点数
// 在池化窗口内寻找最大值
// padding_h_ padding_w_ 池化窗口高宽
// input_h input_w 填充前输入特征图高宽
for (uint32_t w = 0; w < pooling_w; ++w) {
const float* col_ptr = input_channel.colptr(c + w - padding_w_);
for (uint32_t h = 0; h < pooling_h; ++h) {
float current_value = 0.f;
// 检查当前元素是否在有效的输入范围内
if ((h + r >= padding_h_ && w + c >= padding_w_) &&
(h + r < input_h + padding_h_ &&
w + c < input_w + padding_w_)) {
current_value = *(col_ptr + r + h - padding_h_);
}
else {
current_value = std::numeric_limits<float>::lowest(); // 如果不在范围内,赋最小值
}
max_value = max_value > current_value ? max_value : current_value; // 更新最大值
}
}
*(output_channel_ptr + output_row) = max_value; // 将最大值写入输出
}
}
}
对多通道的输入特征图进行逐通道的处理,每次进行一个通道上的最大池化操作,首先获取当前输入张量上的第ic个通道input_channel。然后在输入特征图中进行窗口移动(就如同下图所示),每次纵向移动的步长为stride_h, 每次横向移动的步长为stride_w。
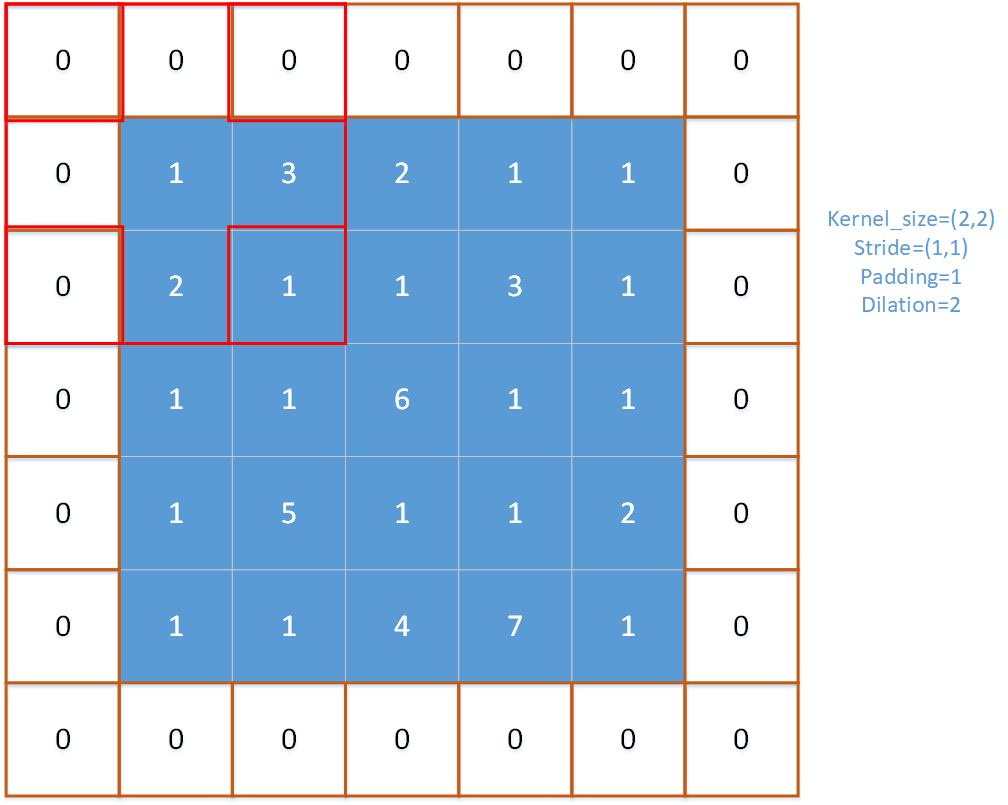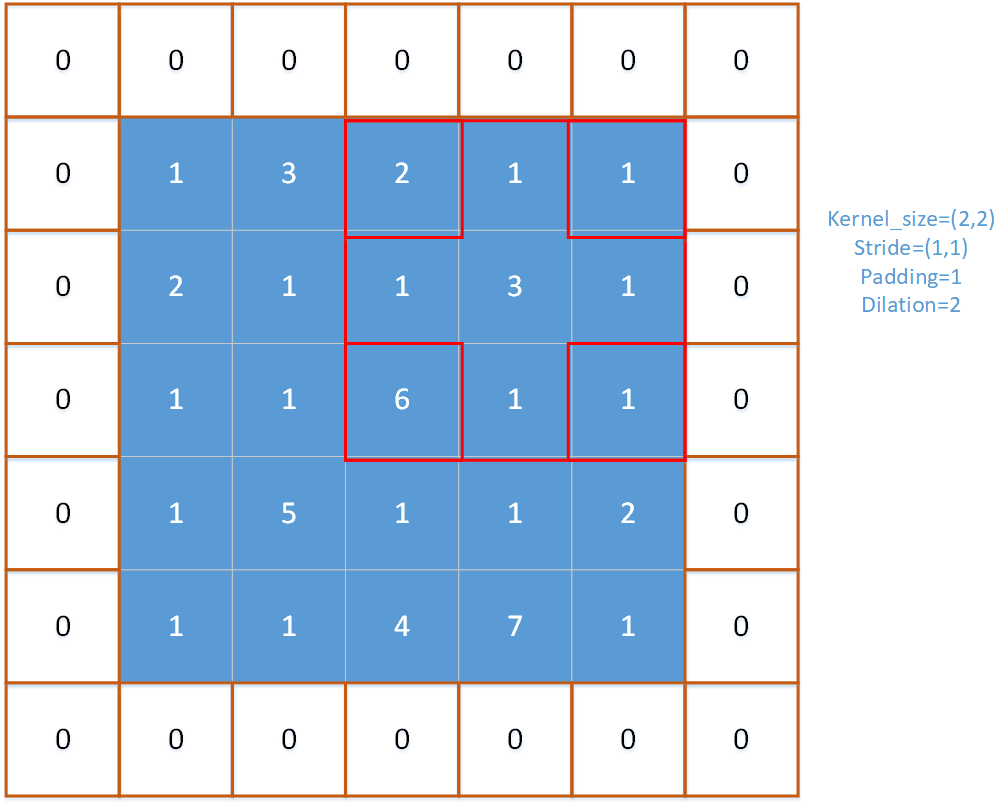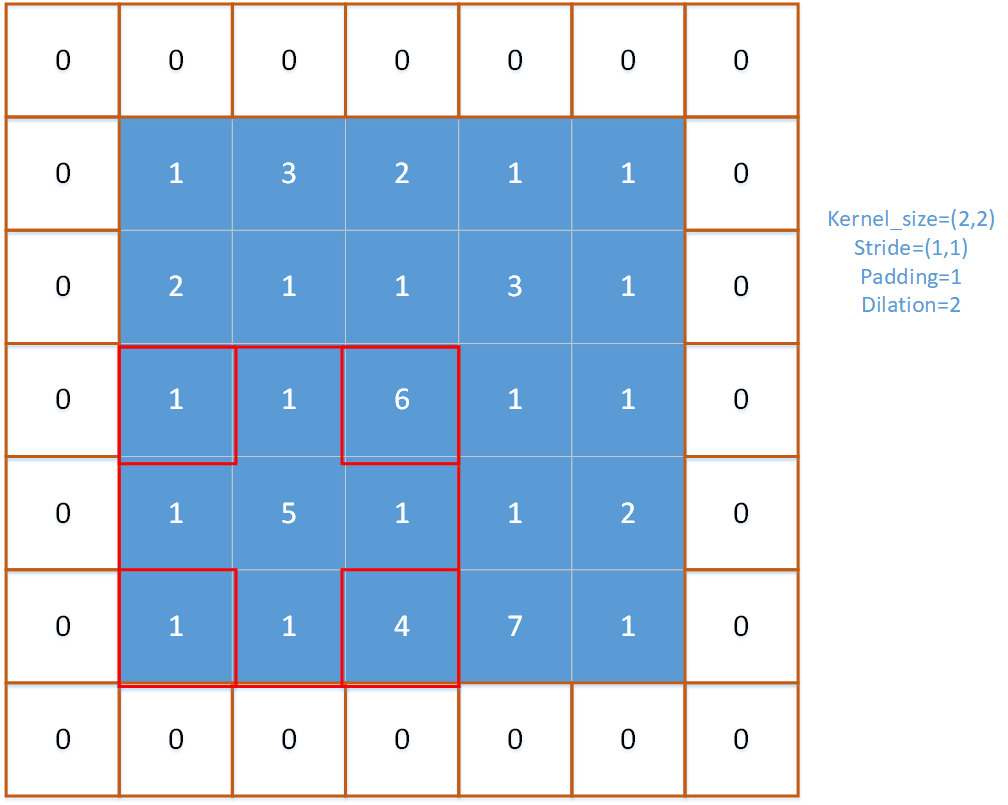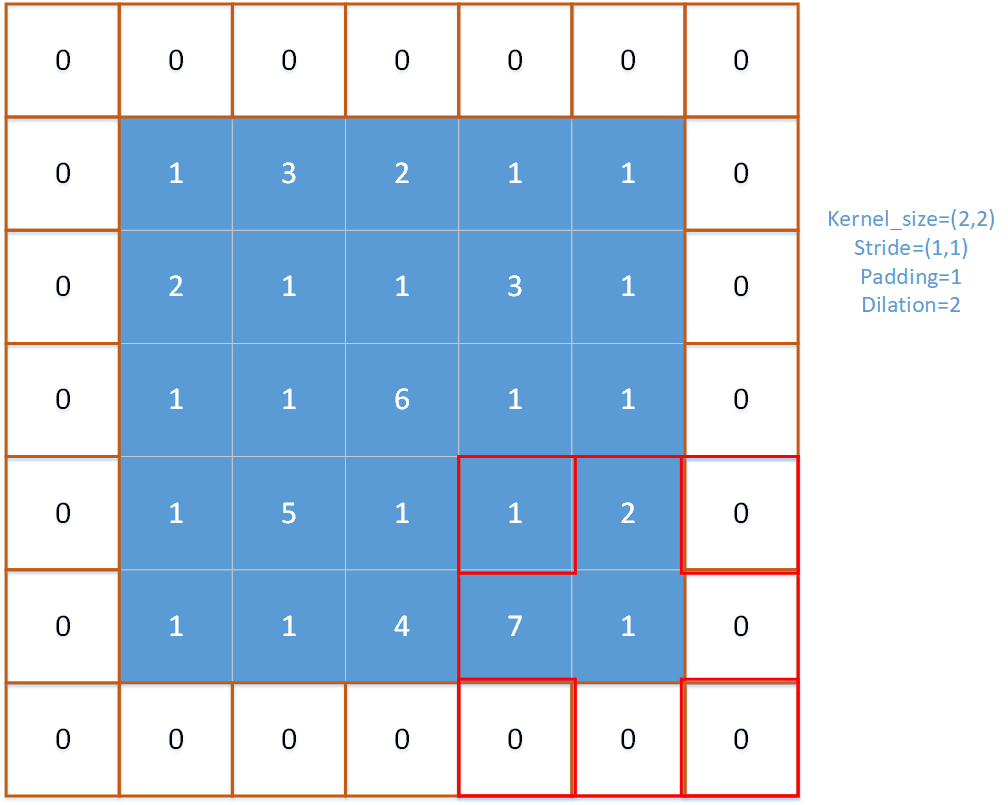
注意以下r,c是指的池化窗口(一般是左上角的格子)在输入特征图的位置,r是窗口的行位置,c是从窗口的位置,w是窗口内的列偏移量,h是窗口内的行偏移量。对一个窗口内的pooling_h × pooling_w个元素求得最大值。在这个内部循环中,有两种情况(使用if判断的地方):
- 当前遍历的元素位于有效范围内,将该元素的值记录下来;
- 当前遍历的元素超出了输入特征图的范围,将该元素的值赋值为一个最小值。
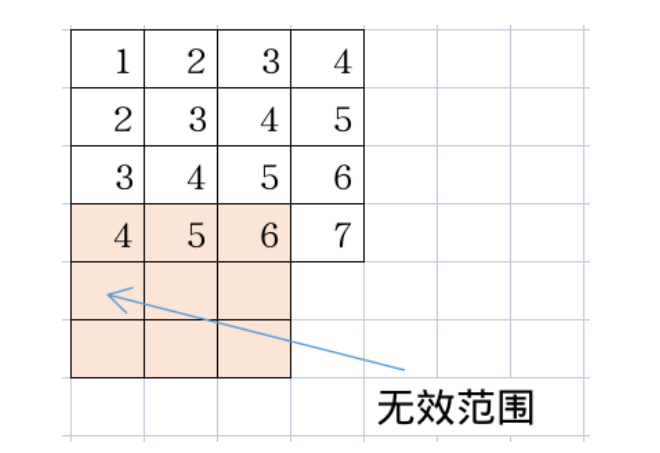
以下是关于无效值范围的图示,可以观察到,在一个窗口大小为3的池化算子中,当该窗口移动到特定位置时,就会出现无效范围,即超出了输入特征图的尺寸限制。
**在内部循环中,当获取到窗口的最大值后,需要将该最大值写入到对应的输出张量中。**以下是输出张量写入的位置索引:
output_data->slice(ic);获得第ic个输出张量;output_channel.colptr(int(c / stride_w_));计算第ic个张量的输出列位置,列的值和当前窗口的位置有关,c表示滑动窗口当前所在的列数.*(output_channel_ptr + int(r / stride_h_)) = max_value;计算输出的行位置,行的位置同样与当前窗口的滑动有关,h表示当前滑动窗口所在的行数。
以下面的图示作为一个例子来讲解对output的输出位置:

在以上情况中,**窗口的滑动步长为2,窗口此时所在的列c等于2,窗口所在的行r等于0。**通过观察下面的输出张量,可以看出在该时刻要写入的输出值为5,其写入位置的计算方法如下:
- 写入位置的列 = c/stride_w = 2/2 =1
- 写入位置的行 = r/stride_h = 0/2 = 0
所以对于该时刻,池化窗口求得的最大值为5,写入的位置为output(0,1).
1.2.2 GetInstance实例化Layer
GetInstance方法:静态方法,用于从 RuntimeOperator 对象中解析参数并创建 MaxPoolingLayer 实例。这通常在模型构建过程中使用。
ParseParameterAttrStatus MaxPoolingLayer::GetInstance(
const std::shared_ptr<RuntimeOperator>& op,
std::shared_ptr<Layer>& max_layer) {
// 检查传入的操作符对象是否为空,如果为空,则打印错误信息并返回失败状态
CHECK(op != nullptr) << "MaxPooling get instance failed, operator is nullptr";
// 获取操作符的参数映射
const std::map<std::string, std::shared_ptr<RuntimeParameter>>& params = op->params;
// 检查参数映射中是否包含 "stride" 参数,如果没有找到则打印错误并返回失败状态
if (params.find("stride") == params.end()) {LOG(ERROR) << "Can not find the stride parameter";
return ParseParameterAttrStatus::kParameterMissingStride;}
// "stride" 参数转换为 RuntimeParameterIntArray 类型
auto stride = std::dynamic_pointer_cast<RuntimeParameterIntArray>(params.at("stride"));
if (!stride) {LOG(ERROR) << "Can not find the stride parameter";
return ParseParameterAttrStatus::kParameterMissingStride;}
......
// 获取 padding, stride 和 kernel_size 的值
const auto& padding_values = padding->value;
const auto& stride_values = stride->value;
const auto& kernel_values = kernel_size->value;
const uint32_t dims = 2; // 期望的维度数量
// 检查 padding 参数的维度是否为 2,否则返回错误
if (padding_values.size() != dims) {LOG(ERROR) << "Can not find the right padding parameter";
return ParseParameterAttrStatus::kParameterMissingPadding;}
......
// 创建 MaxPoolingLayer 对象并初始化 max_layer 指针
max_layer = std::make_shared<MaxPoolingLayer>(
padding_values.at(0), padding_values.at(1), kernel_values.at(0),
kernel_values.at(1), stride_values.at(0), stride_values.at(1));
// 返回参数解析成功状态
return ParseParameterAttrStatus::kParameterAttrParseSuccess;
}
GetInstance 方法的作用是根据传入的 RuntimeOperator对象中的参数,创建并初始化一个 MaxPoolingLayer对象。如果在解析参数的过程中遇到任何问题(例如参数缺失或类型错误),都会返回相应的错误状态,并记录日志信息。最后,成功解析所有参数后,创建一个新的 MaxPoolingLayer对象并返回成功状态。
RuntimeOperator这个数据结构中包含了算子初始化所需的参数和权重信息,首先访问并获取该算子中的所有参数params。在params中获取到了用于初始化池化算子的stride参数,即窗口滑动步长。如果参数中没有stride参数,则返回对应的错误代码。同理可以获取padding、kernel_size参数,注意这些参数`std::shared_ptr<RuntimeParameterIntArray>类型的智能指针,通过下面即可获得对应的参数大小。
// 取出对应的参数值
const auto& padding_values = padding->value;
const auto& stride_values = stride->value;
const auto& kernel_values = kernel_size->value;
最后使用这些参数对池化算子进行初始化,并将其赋值给max_layer参数进行返回。
max_layer = std::make_shared<MaxPoolingLayer>(
padding_values.at(0), padding_values.at(1), kernel_values.at(0),
kernel_values.at(1), stride_values.at(0), stride_values.at(1));
与 ReLU 层相比,MaxPooling 层的额外步骤主要集中在解析和处理涉及步幅、填充、核大小等池化参数上,还需要在执行池化操作前后进行复杂的维度计算和输入输出匹配检查。ReLU 层的逻辑更为简单,几乎不涉及这些额外步骤。
1.2.3 LayerRegistererWrapper注册算子
通过 LayerRegistererWrapper实现了 MaxPoolingLayer类型的层注册,使得在运行时可以根据 “nn.MaxPool2d” 标识符动态创建 MaxPoolingLayer 实例,将最大池化的初始化过程注册到了推理框架中。
LayerRegistererWrapper kMaxPoolingGetInstance("nn.MaxPool2d",
MaxPoolingLayer::GetInstance);
二、卷积算子
2.1 卷积定义
卷积是信号处理和图像处理中常用的运算操作之一。它通过将输入信号(如图像、音频等)与一个卷积核(也称为滤波器或权重)进行相乘和累加的过程,用于在深度神经网络中提取特定的特征。
- 在离散情况下,一维卷积操作可以定义为:
y [ n ] = ∑ k = − ∞ ∞ x [ k ] ⋅ h [ n − k ] y[n] = \sum_{k=-\infty}^{\infty} x[k] \cdot h[n-k] y[n]=k=−∞∑∞x[k]⋅h[n−k]
其中,x表示输入信号,h表示卷积核,y表示输出信号。这个公式表示输出信号中的每个元素 y[n]是通过对输入信号 x进行加权累加计算得到的,计算过程中使用了卷积核 h确定的权重。
-
二维输入(多通道,此处以单通道为例),只需要将卷积定义拓展为二维:
Y [ i , j ] = ∑ m ∑ n H [ m , n ] ⋅ X [ i + m , j + n ] Y[i, j] = \sum_{m} \sum_{n} H[m, n] \cdot X[i+m, j+n] Y[i,j]=m∑n∑H[m,n]⋅X[i+m,j+n]
其中,X表示输入矩阵,H表示卷积核,Y表示输出矩阵,i和j表示输出矩阵中的输出像素坐标,m和n表示卷积核中的坐标,i+m和j+n用于将卷积核和输入矩阵进行对齐,分别表示输入图像中的某个元素坐标。通过这两个偏移量,我们可以确定卷积核在输入矩阵中的位置,并将其与对应位置的像素值相乘,然后求和得到输出矩阵的每个元素 Y[i,j]。
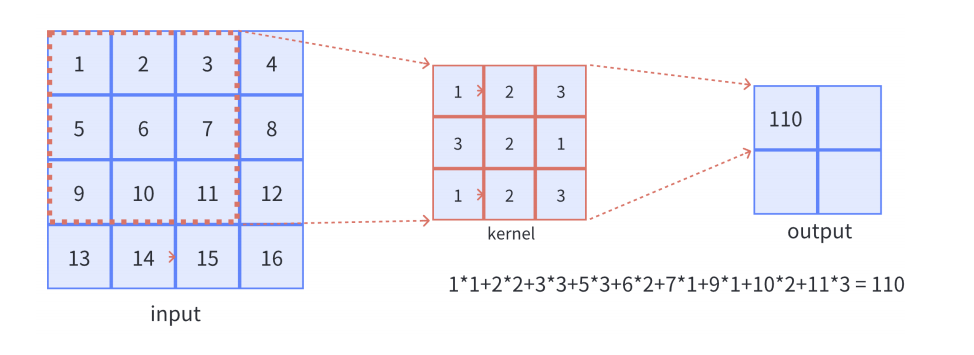
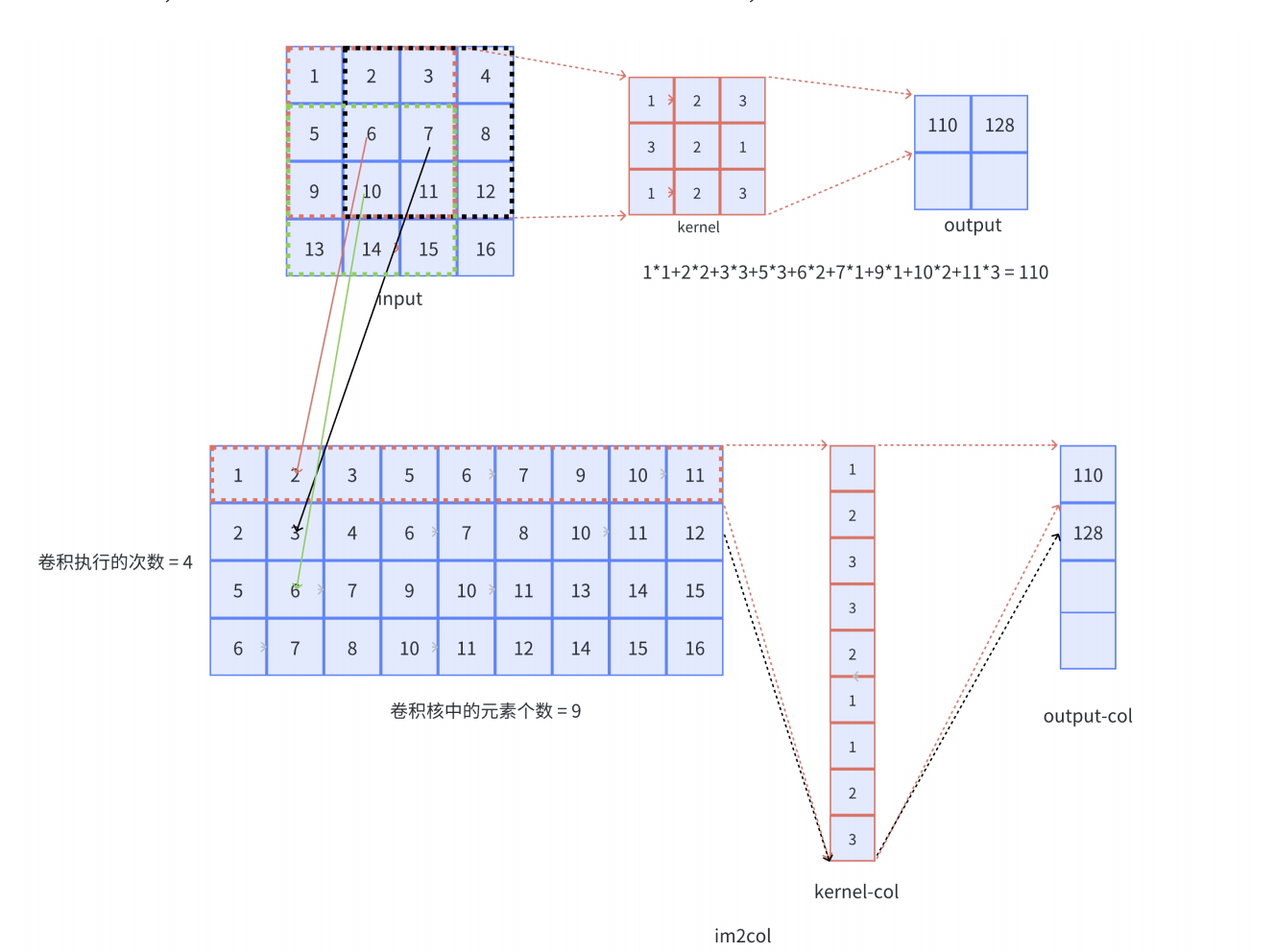
- 对于单通道-单卷积核计算,如下图,对二维卷积的计算过程进行直观展示,卷积核以滑动窗口的形式,从输入中滑过,计算点积并求和,得到卷积后的输出存于
output中。
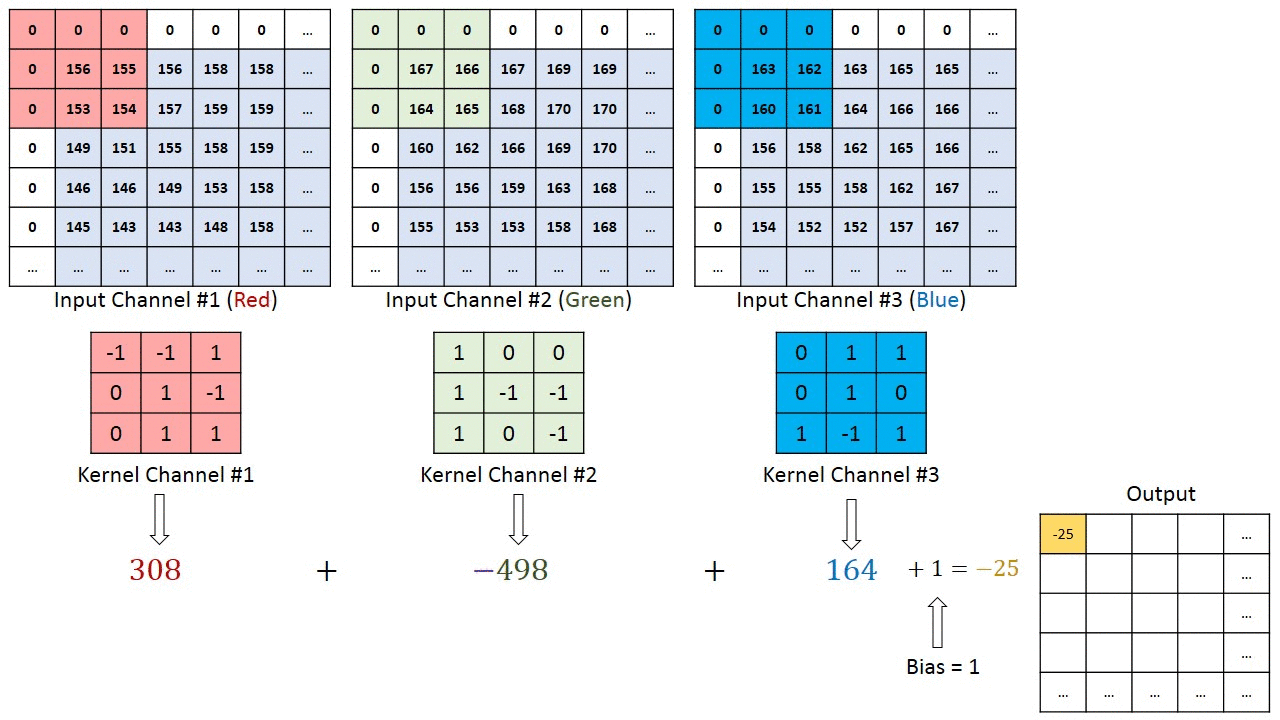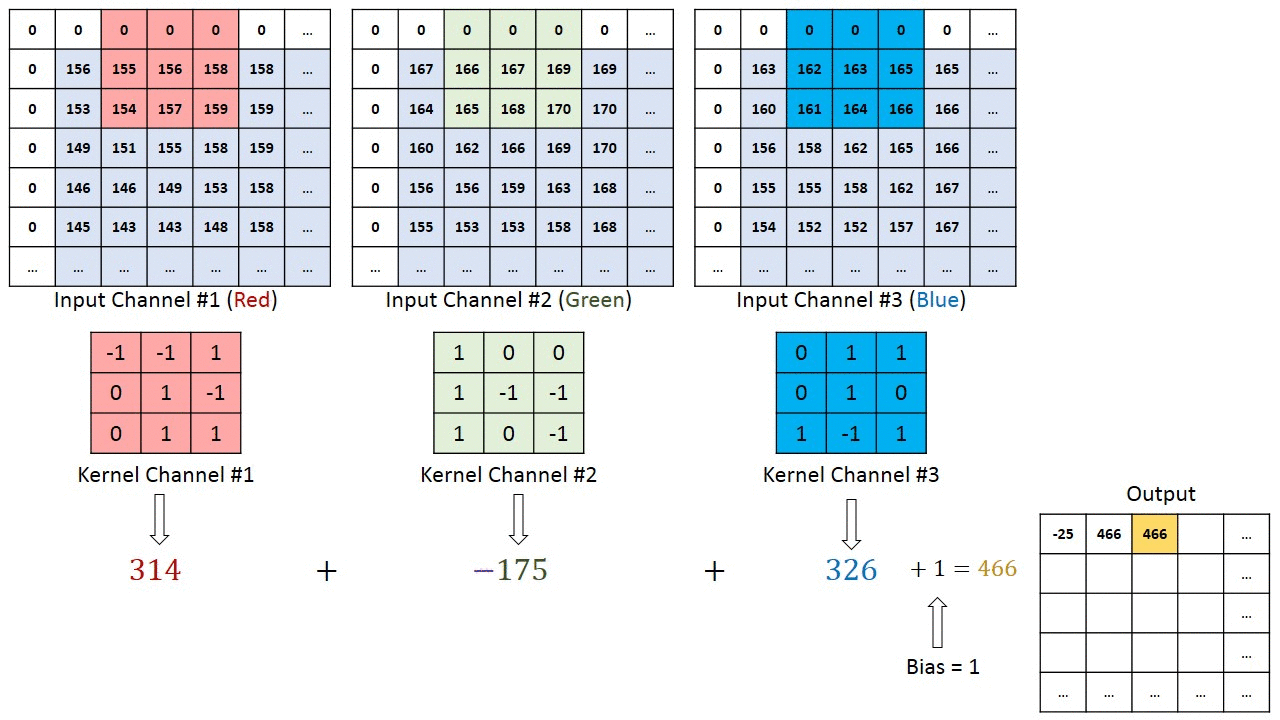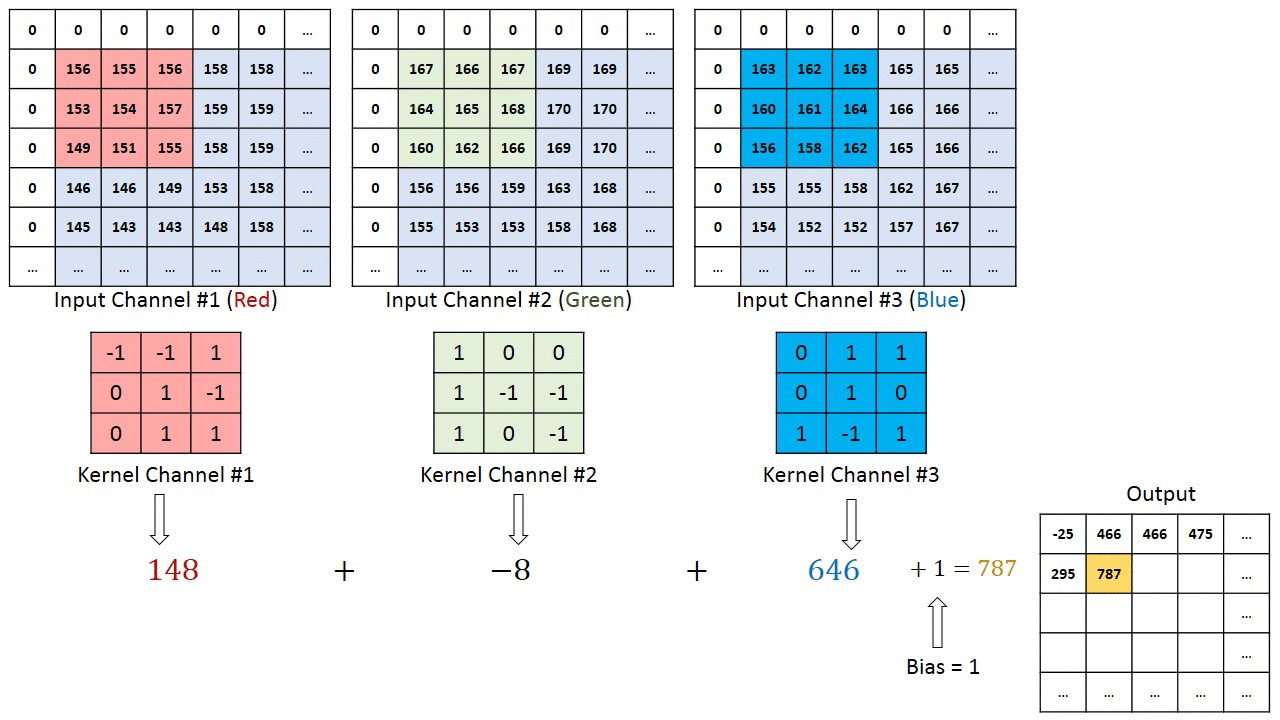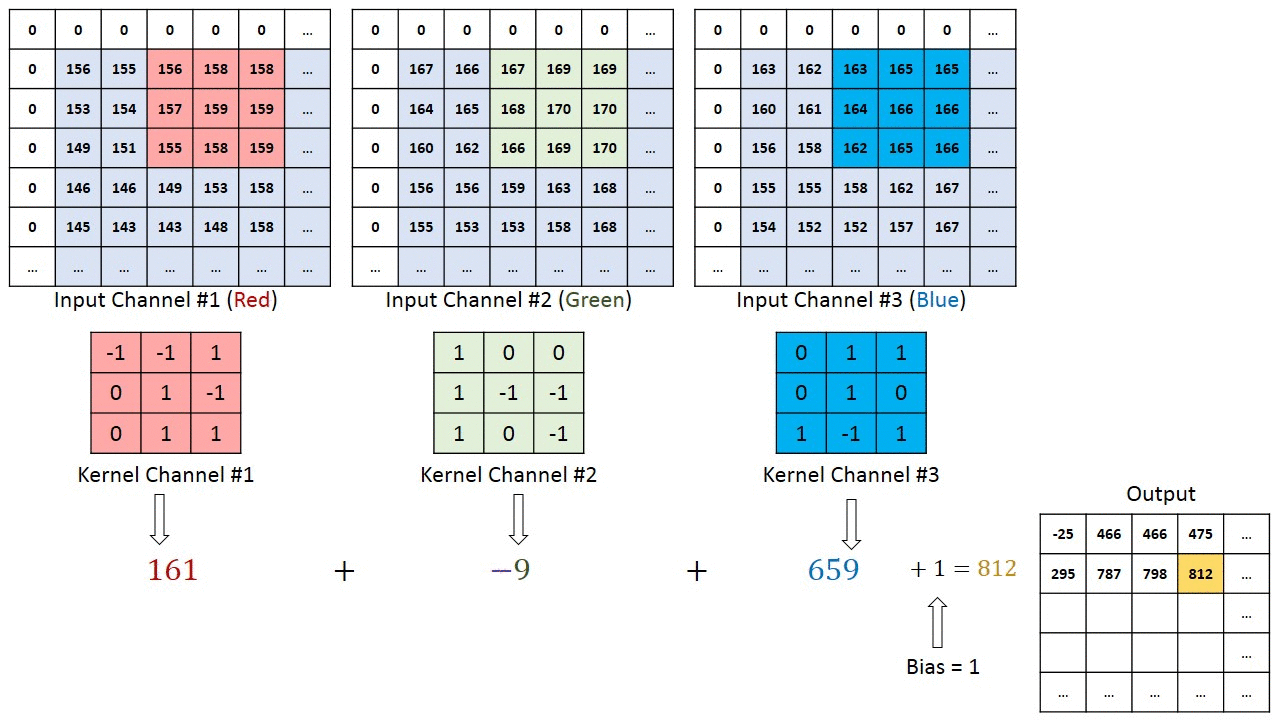
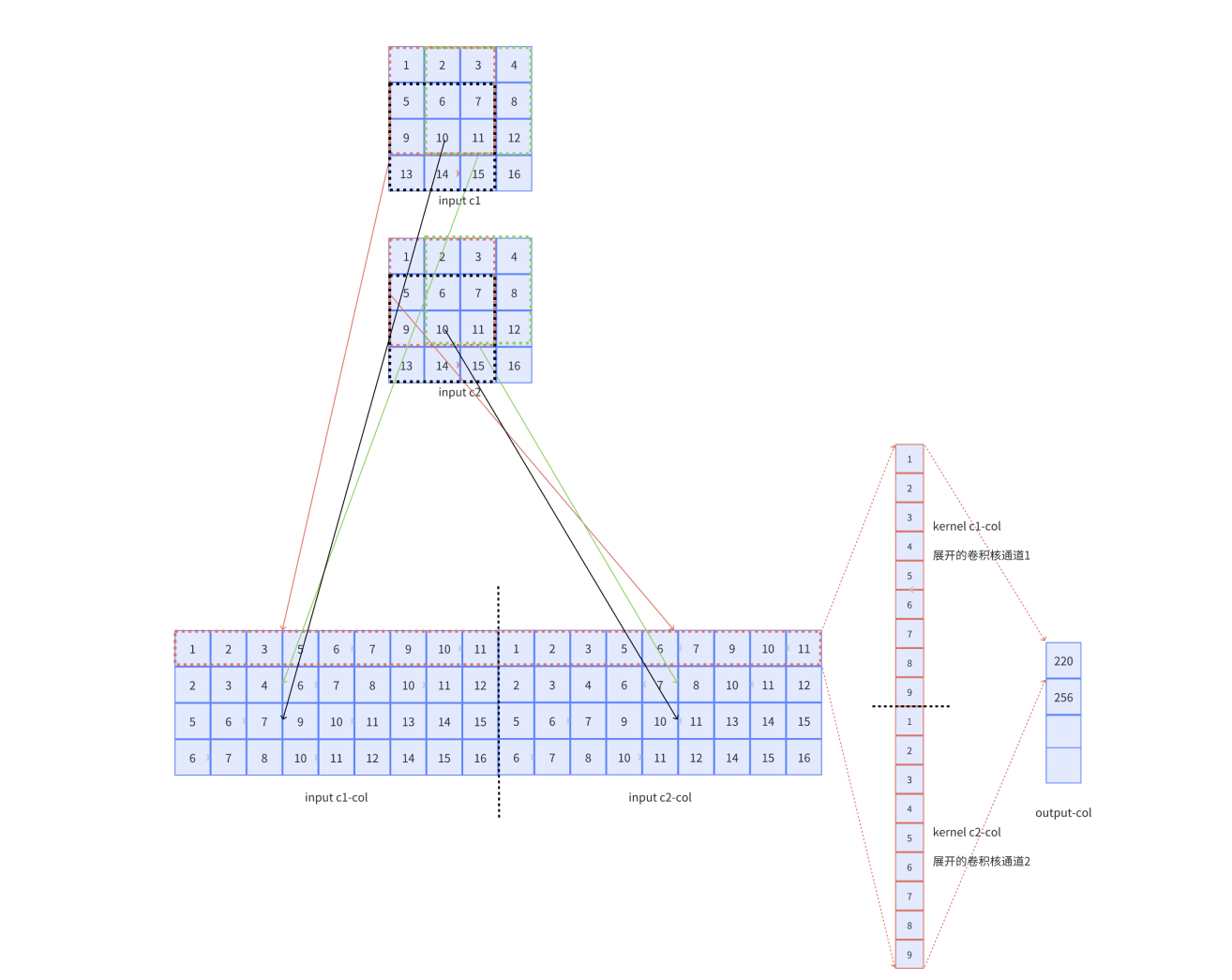
- 对于多通道-单卷积核计算,只需对多个单通道的卷积结果求和即可(请注意,下图中的kernel属于同一个卷积核中的不同通道),此时需要注意的是
输入的通道数与卷积核的通道数相等。 (输出通道数等于卷积核的个数)
如下图所示,可以看到一个多通道的输入和一个多通道的单卷积核进行卷积计算,最后得到了一个单通道的输出output. 输入张量的通道数需要和卷积核的通道数个数相同,这里都是2个通道。input第一个通道和kernel第一个通道 对应位置内求卷积;input第二个通道和kernel第二个通道对应位置内求卷积,最后两者相加,得到对应位置的输出。
-
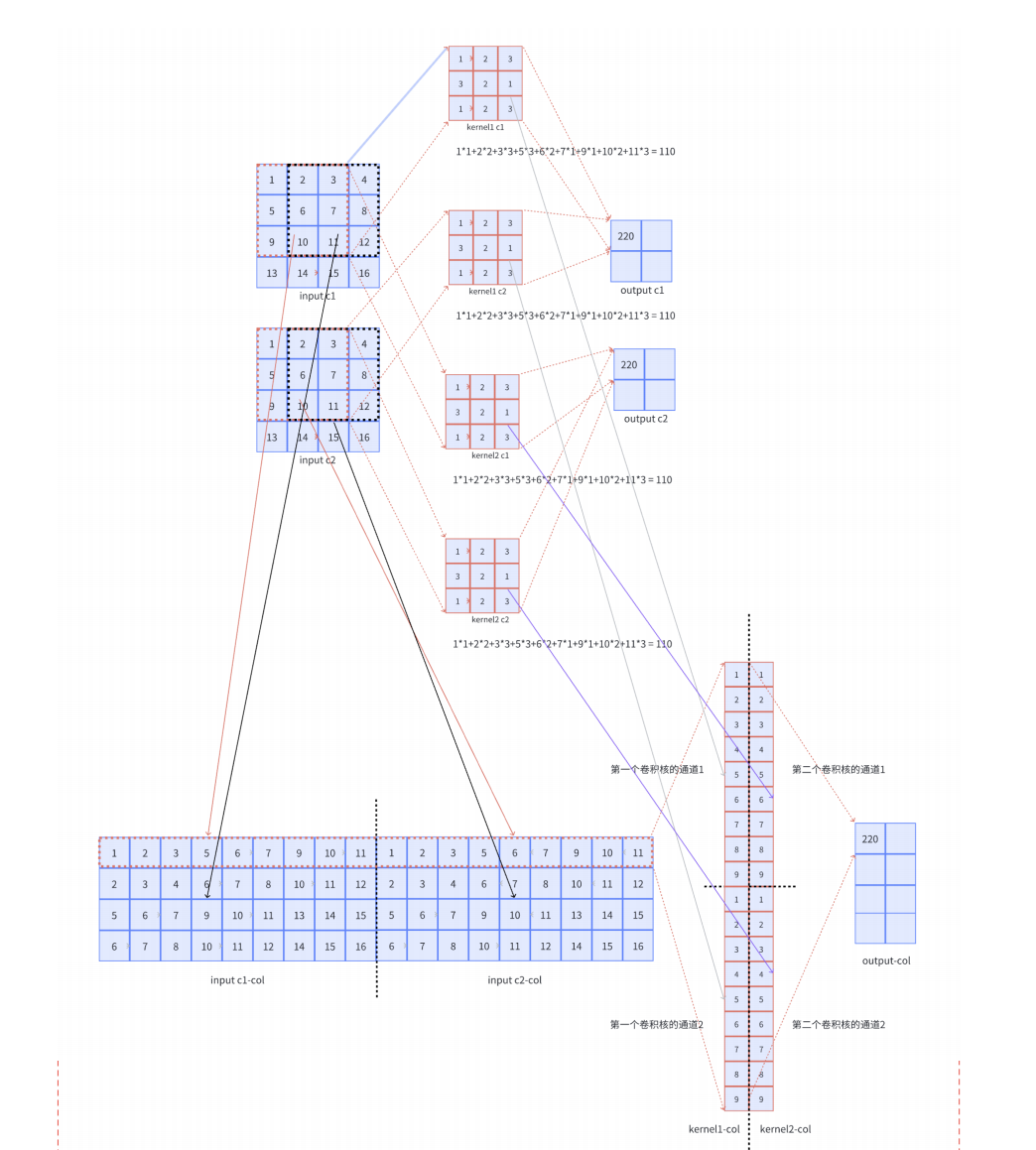
对于多通道-多卷积核计算,只需要知道卷积核个数对应输出通道个数即可。
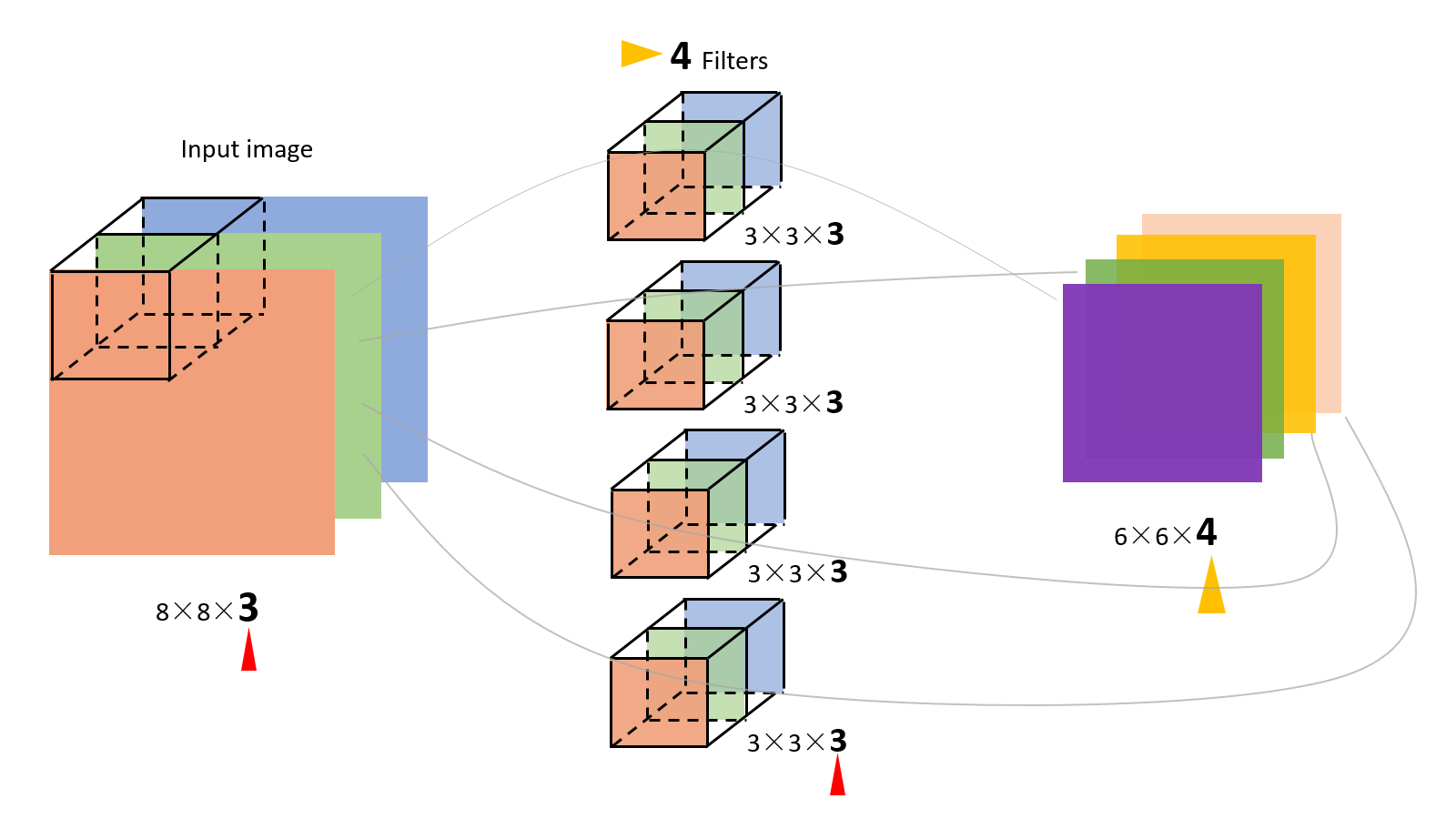
如下图所示,相当于每个卷积核都与输入特征图进行卷积,分别输出一个通道。
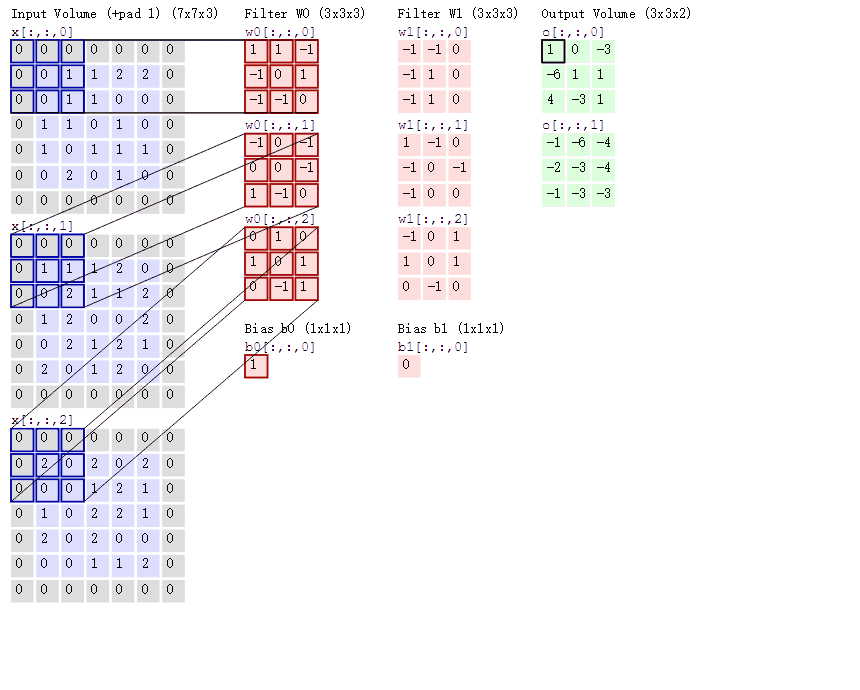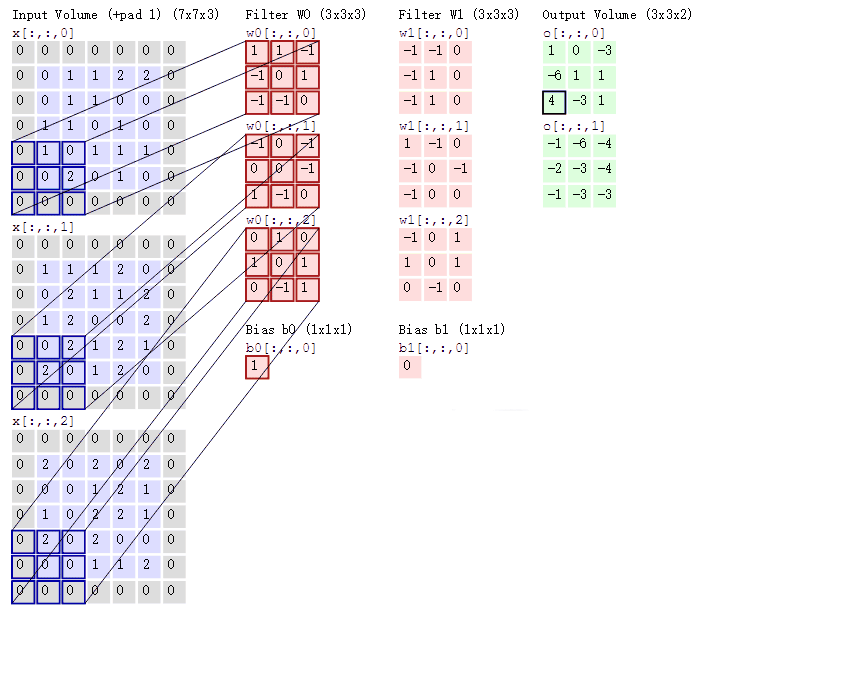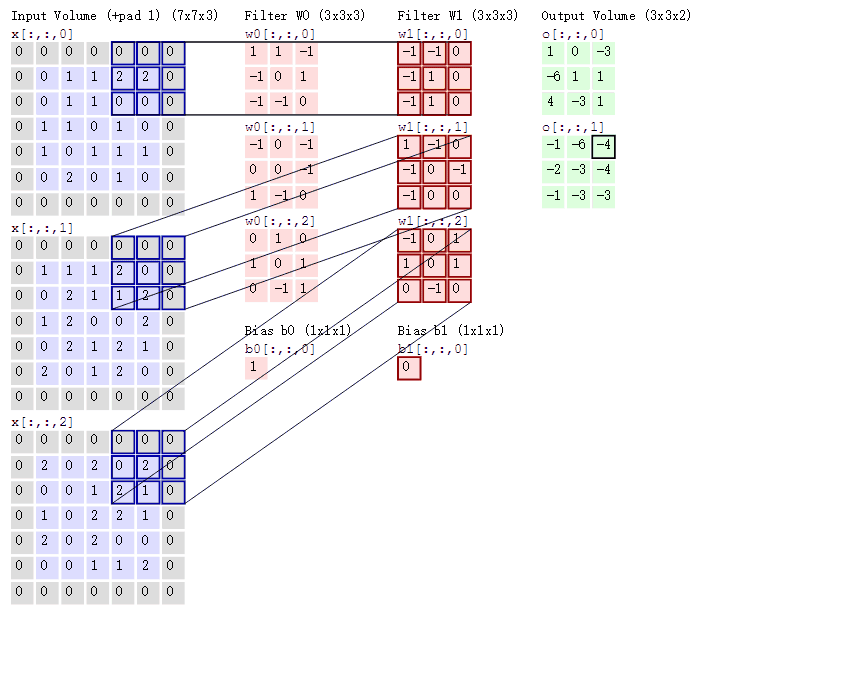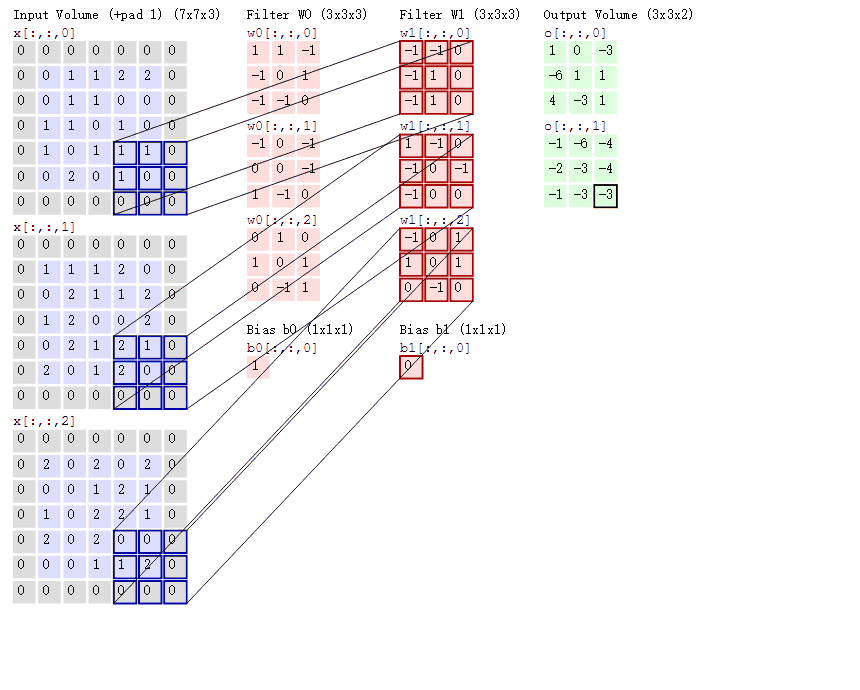
- 组卷积(
group conv),顾名思义就是将卷积分组,即在深度上进行分组,**原本一个卷积核管全部通道,当分组之后,一个卷积核只需要管( input channel / group)个通道。**分组卷积早在AlexNet便得到了应用,Alex认为组卷积能够增加 卷积核之间的对角相关性,并减少训练参数,不容易过拟合,达到类似正则的效果。
总结:**卷积核的通道数等于输入特征图的通道数,而输出特征图的通道数等于卷积核的个数。**在卷积计算中,输入输出大小的维度有以下的对应关系:
假设输入特征图的大小为 H in × W in H_{\text{in}} \times W_{\text{in}} Hin×Win ,池化窗口的大小为 K h × K w K_h \times K_w Kh×Kw ,步幅(Stride)为 S h × S w S_h \times S_w Sh×Sw ,填充(Padding)为 P h × P w P_h \times P_w Ph×Pw ,则输出特征图的大小为 H out × W out H_{\text{out}} \times W_{\text{out}} Hout×Wout。
- 输出特征图的高度 H out H_{\text{out}} Hout :
H out = ⌊ H in + 2 P h − K h S h ⌋ + 1 H_{\text{out}} = \left\lfloor \frac{H_{\text{in}} + 2P_h - K_h}{S_h} \right\rfloor + 1 Hout=⌊ShHin+2Ph−Kh⌋+1
- 输出特征图的宽度 W out W_{\text{out}} Wout :
W out = ⌊ W in + 2 P w − K w S w ⌋ + 1 W_{\text{out}} = \left\lfloor \frac{W_{\text{in}} + 2P_w - K_w}{S_w} \right\rfloor + 1 Wout=⌊SwWin+2Pw−Kw⌋+1
2.2 Im2col优化卷积计算
在卷积神经网络(CNN)中,由于卷积运算的计算量大,因此对卷积操作进行加速成为了非常重要的研究方向。以下是几种主流的卷积加速方法:
-
im2col + GEMM:这是一种
将卷积操作转换为矩阵乘法(GEMM)的技术。它通过将输入张量展开为更大的矩阵(im2col),然后利用高度优化的BLAS库进行矩阵乘法。该方法被Caffe、MXNet等主流计算框架广泛采用,因其利用了现有的高效矩阵乘法算法,通常具有较高的计算速度。 -
Winograd算法:Winograd算法是一种用于小卷积核(如3x3)的高效算法。它在大部分场景中显示出较大的性能优势,目前cudnn中的卷积计算即采用了Winograd方法来加速卷积运算。
-
Strassen算法:这是Volker Strassen在1969年提出的时间复杂度低于O(N^3)的矩阵乘法算法. Strassen算法在处理大卷积核时具有优势,但目前还未在主流开源框架中广泛应用。
-
FFT(快速傅里叶变换):傅里叶变换和快速傅里叶变换在经典图像处理中的卷积操作中经常使用。然而,在卷积神经网络(ConvNet)中,由于卷积核通常较小(如3x3),FFT方法反而会增加计算时间开销,因此很少被用于CNN中的卷积计算。
作为早期的深度学习框架,Caffe中卷积的实现采用的是基于 im2col 的方法,至今仍是卷积重要的优化方法之一。Im2col 是计算机视觉领域中将图片转换成矩阵的矩阵列(column)的计算过程。由于二维卷积的计算比较复杂不易优化,因此在 AI 框架早期,Caffe 使用 Im2col 方法将三维张量转换为二维矩阵,从而充分利用已经优化好的 GEMM 库来为各个平台加速卷积计算。最后,再将矩阵乘得到的二维矩阵结果使用 Col2Im 将转换为三维矩阵输出。

Im2col的核心思想是将卷积计算转化成矩阵计算,利用现有较为成熟的矩阵加速方法实现卷积运算的加速。Im2col+Matmul 方法主要包括两个步骤:
1.使用 Im2col 将输入矩阵展开一个大矩阵,矩阵每一列表示卷积核需要的一个输入数据。
2.使用上面转换的矩阵进行 Matmul 运算,得到的数据就是最终卷积计算的结果。
算法过程:
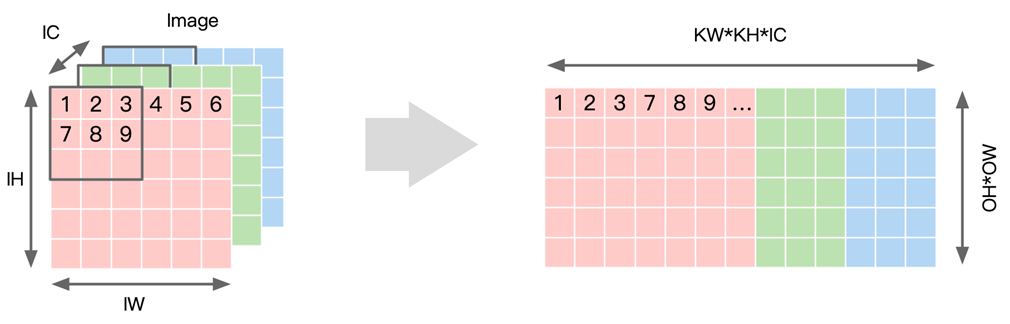
卷积操作转换为矩阵相乘,对 Kernel 和 Input 进行重新排列。将输入数据按照卷积窗进行展开并存储在矩阵的列中,多个输入通道的对应的窗展开之后将拼接成最终输出 Matrix 的一列:
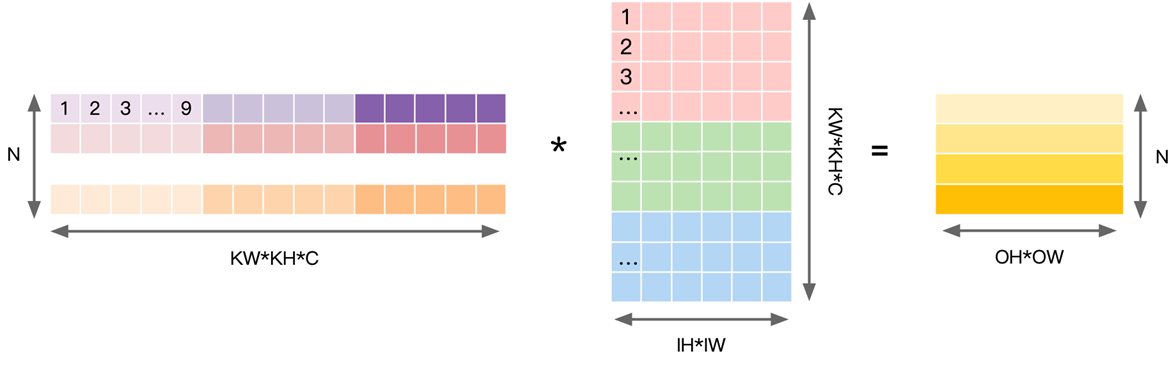
- 对 Input 进行重排,得到的矩阵见右侧,行数对应输出 OH*OW 个数;每个行向量里,先排列计算一个输出点所需要输入上第一个通道的 KH*KW 个数据,再按次序排列之后通道,直到通道 IC。
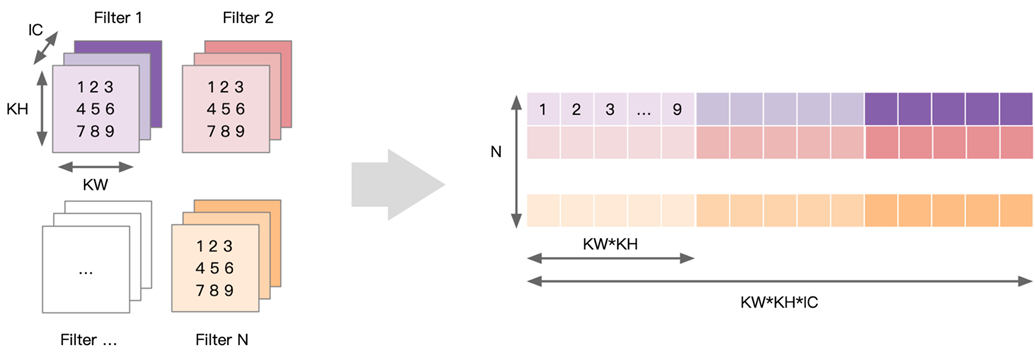
- 对权重数据进行重排,即以卷积的 stride 为步长展开后续卷积窗并存在 Matrix 下一列。
将 N 个卷积核展开为权重矩阵的一行,因此共有 N 行,每个行向量上先排列第一个输入通道上KH*KW 数据,再依次排列后面的通道直到 IC。
- 通过数据重排,完成 Im2col 的操作之后会得到一个输入矩阵,卷积的 Weights 也可以转换为一个矩阵,卷积的计算就可以转换为两个矩阵相乘的求解,得到最终的卷积计算结果。
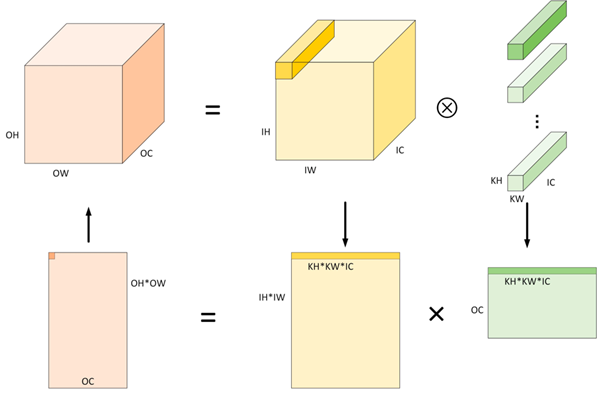
Im2col 算法计算卷积的过程,具体过程如下(简单起见忽略 Padding 的情况,即认为 OH=IH,OW=IW):
1.将输入由 N×IH×IW×IC 根据卷积计算特性展开成 (OH×OW)×(N×KH×KW×IC) 形状二维矩阵。显然,转换后使用的内存空间相比原始输入多约 KH∗KW−1 倍;
2.权重形状一般为 OC×KH×KW×IC 四维张量,可以将其直接作为形状为 (OC)×(KH×KW×IC) 的二维矩阵处理;
3.对于准备好的两个二维矩阵,将 (KH×KW×IC) 作为累加求和的维度,运行矩阵乘可以得到输出矩阵 (OH×OW)×(OC);
4.将输出矩阵 (OH×OW)×(OC) 在内存布局视角即为预期的输出张量 N×OH×OW×OC,或者使用 Col2Im 算法变为下一个算子输入 N×OH×OW×OC
Im2col 计算卷积使用 GEMM 的代价是额外的内存开销。使用 Im2col 将三维张量展开成二维矩阵时,原本可以复用的数据平坦地分布到矩阵中,将输入数据复制了 KH∗KW−1 份。转化成矩阵后,可以在连续内存和缓存上操作,而且有很多库提供了高效的实现方法(BLAS、MKL),Numpy 内部基于 MKL 实现运算的加速。
在实际实现时,离线转换模块实现的时候可以预先对权重数据执行 Im2col 操作,Input Data Im2col和GEMM的数据重排会同时进行,以节省运行时间。
下图展示单通道卷积的Im2col展开方式:对于输入,每行代表一个卷积核窗口扫过的区域,展开的行数为input-col,也就是卷积总执行次数,每行的列数为一个卷积核元素的个数,本例中input被展开为一个4x9的矩阵;对于卷积核,一个卷积核展成一列,本例中卷积核被展开为一个9x1的向量;卷积计算就被成功转化成矩阵计算,
- 多通道的输入单卷积核
- 多通道输入多卷积核
参考资料:https://www.bilibili.com/video/BV1Q4411T7aD/
2.3 分组卷积
分组卷积(Grouped Convolution) 是一种通过减少计算量来加速卷积神经网络的方法。在标准卷积中,输入通道和输出通道之间是完全连接的,即每个输出通道都与所有输入通道相连接并参与卷积计算。而在分组卷积中,输入通道和输出通道被分为若干组,每组的输入通道只与相应的输出通道进行卷积运算。
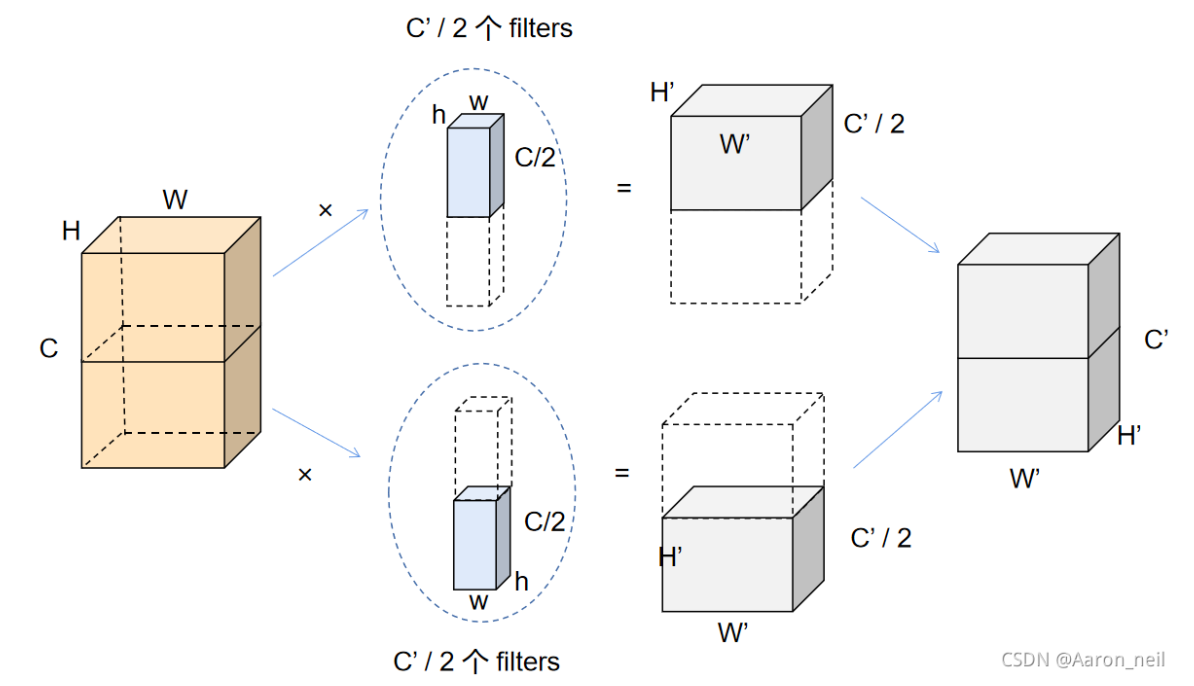
分组卷积 的表示如上图(group=2) ,每个filters组,包含 C’/2个 数量的filter, 每个filter 的通道数为传统2D-卷积filter的一半。每个filters组作用于原来 W × H × C 对应通道数的一半,也就是 W × H × C/2。最终每个filters组对应输出输出 C’ / 2 个通道的特征。最后将通道堆叠得到了最终的 C’个通道,实现了和上述标准2D 卷积一样的效果。
对于分组卷积的卷积计算,属于group1的两个卷积核与属于group1的输入特征图通道展开后进行相乘,属于group2的两个卷积核与属于group2的输入特征图通道展开后进行相乘。

2.4 Im2Col实现
因为armadillo自身是列主序的,所以这里相当于在做
Im2Row。
Im2Col的代码实现如下:
arma::fmat ConvolutionLayer::Im2Col(sftensor input, uint32_t kernel_w,
uint32_t kernel_h, uint32_t input_w,
uint32_t input_h, uint32_t input_c_group,
uint32_t group, uint32_t row_len,
uint32_t col_len) const {
// 创建一个大小为 (input_c_group * row_len, col_len) 的矩阵
arma::fmat input_matrix(input_c_group * row_len, col_len);
// 计算输入图像的填充后的高度和宽度
const uint32_t input_padded_h = input_h + 2 * padding_h_;
const uint32_t input_padded_w = input_w + 2 * padding_w_;
// 定义填充值为 0
const float padding_value = 0.f;
// 遍历输入通道组中的每个通道
for (uint32_t ic = 0; ic < input_c_group; ++ic) {
// 获取当前通道的指针,指向输入张量的原始数据
float* input_channel_ptr =
input->matrix_raw_ptr(ic + group * input_c_group);
// 初始化当前列的索引
uint32_t current_col = 0;
// 计算当前通道在输出矩阵中的行偏移量
uint32_t channel_row = ic * row_len;
// 遍历填充后的输入图像的宽度,步长为 stride_w_
for (uint32_t w = 0; w < input_padded_w - kernel_w + 1; w += stride_w_) {
// 遍历填充后的输入图像的高度,步长为 stride_h_
for (uint32_t r = 0; r < input_padded_h - kernel_h + 1; r += stride_h_) {
// 获取当前列的指针,指向输出矩阵中的当前列
float* input_matrix_ptr =
input_matrix.colptr(current_col) + channel_row;
// 增加列索引
current_col += 1;
// 遍历卷积核的宽度
for (uint32_t kw = 0; kw < kernel_w; ++kw) {
// 计算当前宽度位置的区域偏移量
const uint32_t region_w = input_h * (w + kw - padding_w_);
// 遍历卷积核的高度
for (uint32_t kh = 0; kh < kernel_h; ++kh) {
// 判断是否在有效输入区域内
if ((kh + r >= padding_h_ && kw + w >= padding_w_) &&
(kh + r < input_h + padding_h_ &&
kw + w < input_w + padding_w_)) {
// 获取区域指针,指向输入张量的当前区域
float* region_ptr =
input_channel_ptr + region_w + (r + kh - padding_h_);
// 将区域值复制到输出矩阵中
*input_matrix_ptr = *region_ptr;
} else {
// 如果在填充区域,则填充为0
*input_matrix_ptr = padding_value;
}
// 移动输出矩阵指针到下一行
input_matrix_ptr += 1;
}
}
}
}
}
// 返回填充后的输入矩阵
return input_matrix;
}
函数输入参数:
-
sftensor input: 输入张量,通常表示输入特征图,包含多个通道。
-
uint32_t kernel_w, kernel_h: 卷积核的宽度和高度。
-
uint32_t input_w, input_h: 输入特征图的宽度和高度。
-
uint32_t input_c_group: 每组的输入通道数。
-
uint32_t group: 当前处理的分组索引。
-
uint32_t row_len: 每个输入通道在转换后的矩阵中的行数,即卷积窗口大小 (
kernel_h * kernel_w)。 -
uint32_t col_len: 转换后的矩阵的列数,卷积窗口滑动的次数也,对应于特征图上卷积窗口的位置数量。
对于下图的情况,row_len等于9,表示展开后的行数;col_len等于4,表示卷积窗口滑动的次数。
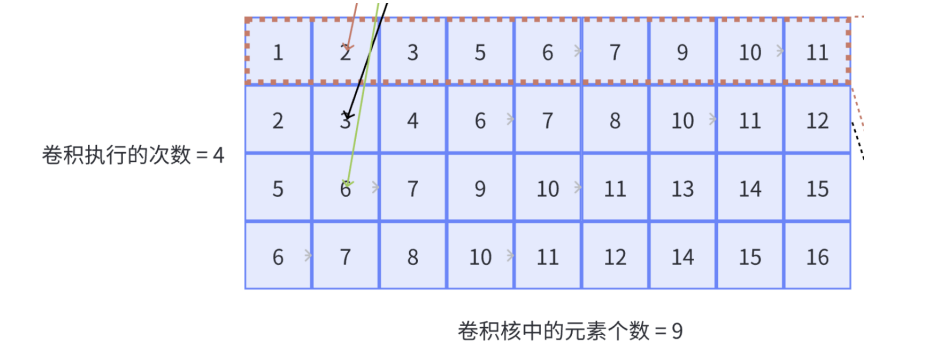
arma::fmat input_matrix(input_c_group * row_len, col_len);
const uint32_t input_padded_h = input_h + 2 * padding_h_;
const uint32_t input_padded_w = input_w + 2 * padding_w_;
首先初始化矩阵input_matrix,用于存储对输入图像展开后的矩阵, input_padded_*表示输入填充后的尺寸大小。这里的input_matrix行数等于
i
n
p
u
t
_
c
_
g
r
o
u
p
×
r
o
w
_
l
e
n
input\_c\_group\times row\_len
input_c_group×row_len,从下方的图中可以看出,对于多输入通道的情况,它的列数等于输入通道数和卷积核相乘(因为armadillo是列主序的,实际执行Im2Row,所以行列相反),它的行数等于col_len(行列相反),也就是卷积窗口进行滑动的次数。
函数通过嵌套循环遍历每一个输入通道的每一个位置的每一个卷积核区域,ic 用来遍历当前组的所有输入通道。
for (uint32_t ic = 0; ic < input_c_group; ++ic) {
// 获取当前通道的输入
float* input_channel_ptr =
input->matrix_raw_ptr(ic + group * input_c_group);
uint32_t current_col = 0;
// 当前通道的展开应该放在哪个行位置
// 因为多个通道同一位置是横向摆放的
uint32_t channel_row = ic * row_len;
// 表示在一个输入通道上进行滑动
for (uint32_t w = 0; w < input_padded_w - kernel_w + 1; w += stride_w_) {
for (uint32_t r = 0; r < input_padded_h - kernel_h + 1; r += stride_h_) {
float* input_matrix_ptr =
input_matrix.colptr(current_col) + channel_row;
然后遍历输入特征图的每一个卷积位置,通过遍历输入特征图的宽度 w 和高度 r,对于每一个 (w, r) 位置上的卷积操作,提取出一个 kernel_w x kernel_h 的子区域,将该子区域的数据存入 input_matrix的适当位置。
对于每一个卷积核位置(kw, kh),计算该位置在输入特征图中的实际坐标,并提取出相应的像素值。
for (uint32_t kw = 0; kw < kernel_w; ++kw) {
// w是窗口所在的列 kw是窗口内当前的偏移量
// r是卷积窗口所在的行,kh是窗口内的行偏移量
const uint32_t region_w = input_h * (w + kw - padding_w_);
for (uint32_t kh = 0; kh < kernel_h; ++kh) {
if ((kh + r >= padding_h_ && kw + w >= padding_w_) &&
(kh + r < input_h + padding_h_ &&
kw + w < input_w + padding_w_)) {
float* region_ptr = //指向窗口内元素的位置
input_channel_ptr + region_w + (r + kh - padding_h_);
*input_matrix_ptr = *region_ptr;
}
...
input_matrix_ptr += 1;
input_matrix_ptr依次指向上图中channel_row之后的各个位置,用于存放展开后的各元素。
接下来,需要处理卷积窗口内的所有元素。首先,要定位到当前需要展开的元素region_ptr, 也就是下图黄色范围。定位的方法是先将指针定位到输入通道的列,即
i
n
p
u
t
_
c
h
a
n
n
e
l
_
p
t
r
+
(
w
+
k
w
−
p
a
d
d
i
n
g
_
w
)
input\_channel\_ptr + (w + kw - padding\_w)
input_channel_ptr+(w+kw−padding_w),然后再将指针定位到输入通道数的行,即
i
n
p
u
t
_
c
h
a
n
n
e
l
_
p
t
r
+
(
r
+
k
h
−
p
a
d
d
i
n
g
_
h
)
input\_channel\_ptr+(r + kh - padding\_h)
input_channel_ptr+(r+kh−padding_h)。这样就能得到当前需要处理元素的内存地址。

region_ptr表示正在展开的输入特征图的内存索引位置,而input_matrix_ptr表示展开后存放元素的位置的指针。
最后函数返回input_matrix 是一个重排后的矩阵,每一列对应输入特征图的一个卷积窗口位置,而每一行对应每个通道在不同卷积窗口位置的值。
在处理分组卷积时,input_c_group和 group 参数确保了输入通道的分组处理。每一组通道独立进行处理,并且生成独立的 input_matrix子矩阵,最后可以与卷积核对应分组的权重矩阵进行矩阵乘法,从而完成分组卷积的计算。
2.5 卷积算子实现
Forward 函数的主要作用是执行卷积层的前向传播。它涉及输入张量的验证与处理、卷积核的初始化与检查、矩阵转换、卷积操作的计算(包括分组卷积的处理),并将结果存储到输出张量中。
InferStatus ConvolutionLayer::Forward(
const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
std::vector<std::shared_ptr<Tensor<float>>>& outputs)
首先是对批次数据逐个处理。
for (uint32_t i = 0; i < batch_size; ++i) {
...
...
}
const uint32_t input_c = input->channels();
const uint32_t input_padded_h = input->rows() + 2 * padding_h_;
const uint32_t input_padded_w = input->cols() + 2 * padding_w_;
const uint32_t output_h =
std::floor((int(input_padded_h) - int(kernel_h)) / stride_h_ + 1);
const uint32_t output_w =
std::floor((int(input_padded_w) - int(kernel_w)) / stride_w_ + 1);
...
uint32_t col_len = output_h * output_w;
在以上的代码中,计算了输入张量的尺寸,输出张量的尺寸以及col_len(也就是卷积窗口执行计算的次数)。
// 4 /2 = 2
uint32_t input_c_group = input_c / groups_;
// 分组卷积里才有的情况
for (uint32_t g = 0; g < groups_; ++g) {
const auto& input_matrix =
// 展开属于一个group中的所有输入通道
Im2Col(input, kernel_w, kernel_h, input->cols(), input->rows(),
input_c_group, g, row_len, col_len);
std::shared_ptr<Tensor<float>> output_tensor = outputs.at(i);
if (output_tensor == nullptr || output_tensor->empty()) {
output_tensor =
std::make_shared<Tensor<float>>(kernel_count, output_h, output_w);
outputs.at(i) = output_tensor;
}
在以上的代码中,对group进行迭代遍历,其中g表示当前的组号,input_c_group表示每组卷积需要处理的通道数,Im2Col函数中会对属于该组的输入通道进行展开。
for (uint32_t g = 0; g < groups_; ++g) {
...
...
const uint32_t kernel_count_group_start = kernel_count_group * g;
for (uint32_t k = 0; k < kernel_count_group; ++k) {
arma::frowvec kernel;
if (groups_ == 1) {
// 非分组的情况
kernel = kernel_matrix_arr_.at(k);
} else {
// 分组卷积的情况
kernel = kernel_matrix_arr_.at(kernel_count_group_start + k);
}
ConvGemmBias(input_matrix, output_tensor, g, k, kernel_count_group,
kernel, output_w, output_h);
}
}
kernel_count_group是分组卷积中,每组卷积分得的卷积核个数,所以在内层for循环中,使用kernel_count_goup, k等变量定位到对应的卷积核。
k e r n e l i n d e x = k + g × k e r n e l c o u n t g r o u p kernel \, index=k+g \times kernel\,count\,group kernelindex=k+g×kernelcountgroup
这里对属于同一组的输入通道和卷积核(每组卷积核的个数是kernel_count_group个)进行逐一的相乘,也就是说,这里进行相乘的卷积核和输入通道都属于同一个group。
小结:
-
首先计算得到了每个组需要处理的通道数input_channel_group,随后再对该组这些输入通道进行展开(
Im2Col函数)。 -
获取到1中对应的卷积核组,将它们逐个取出,取出的方式为:
k e r n e l i n d e x + g r o u p × k e r n e l c o u n t g r o u p kernel\,index+group\times kernel\,count\,group kernelindex+group×kernelcountgroup
-
然后,将取出的同组每个卷积核与步骤1中得到的同一组输入通道进行相乘,得到结果。
2.5.1 GEMM实现
ConvGemmBias方法是 ConvolutionLayer类中处理卷积核矩阵与输入矩阵乘法并添加偏置的函数。函数接受多个参数来执行这些计算,并将结果存储在输出张量中。
void ConvolutionLayer::ConvGemmBias(
const arma::fmat& input_matrix, sftensor output_tensor, uint32_t group,
uint32_t kernel_index, uint32_t kernel_count_group,
const arma::frowvec& kernel, uint32_t output_w, uint32_t output_h) const {
// 从 output_tensor 中获取对应分组和卷积核索引的矩阵,该矩阵大小为 output_h * output_w
arma::fmat output(
output_tensor->matrix_raw_ptr(kernel_index + group * kernel_count_group),
output_h, output_w, false, true);
// 检查输出矩阵的大小是否正确
CHECK(output.size() == output_h * output_w)
<< "卷积层中,输出矩阵的大小应为 output_h x output_w";
// 如果启用了偏置并且偏置不为空,执行带偏置的矩阵乘法
if (!this->bias_.empty() && this->use_bias_) {
std::shared_ptr<Tensor<float>> bias;
bias = this->bias_.at(kernel_index);
if (bias != nullptr && !bias->empty()) {
float bias_value = bias->index(0);
// 使用偏置进行卷积计算
output = kernel * input_matrix + bias_value;
} else {
LOG(FATAL) << "偏置张量为空或为 nullptr";
}
} else {
// 不使用偏置的卷积计算
output = kernel * input_matrix;
}
}
参数说明:
-
input_matrix: 卷积操作前处理过的输入矩阵,即展开后的输入特征
-
output_tensor: 用来存储卷积计算结果的输出张量
-
group: 当前进行
Im2Col的组(group)数 -
kernel_index: 当前处理的卷积核索引。
-
kernel_count_group: 每个分组中的卷积核数量。
-
kernel: 当前使用的卷积核。
-
output_*: 输出张量的宽度和高度。
从 output_tensor中提取当前分组和卷积核对应的矩阵,大小为 output_h * output_w。如果启用了偏置,并且偏置存在,则将偏置值添加到卷积结果中。如果没有启用偏置,直接执行矩阵乘法 kernel * input_matrix 并将结果存入输出矩阵。
arma::fmat output(
output_tensor->matrix_raw_ptr(kernel_index + group * kernel_count_group),
output_h, output_w, false, true);
以上的代码中定位了输出矩阵所在的位置,kernel_count_group表示属于一个group的卷积核数量。kernel_index表示当前group内的卷积核索引,group表示当前的组数,所以使用
k
e
r
n
e
l
i
n
d
e
x
+
g
r
o
u
p
×
k
e
r
n
e
l
c
o
u
n
t
g
r
o
u
p
kernel\,index+group\times kernel\,count\,group
kernelindex+group×kernelcountgroup索引到当前卷积核对应的输出矩阵位置。
if (!this->bias_.empty() && this->use_bias_) {
std::shared_ptr<Tensor<float>> bias;
bias = this->bias_.at(kernel_index);
if (bias != nullptr && !bias->empty()) {
float bias_value = bias->index(0);
output = kernel * input_matrix + bias_value;
} else {
LOG(FATAL) << "Bias tensor is empty or nullptr";
}
} else {
output = kernel * input_matrix;
}
然后将展开后的输入矩阵input_matrix和展开后的卷积核kernel相乘,得到结果矩阵output。
2.5.2 卷积算子的实例化
使用LayerRegistererWrapper将该算子的实例化过程注册到了深度学习推理框架中。
LayerRegistererWrapper kConvGetInstance("nn.Conv2d",
ConvolutionLayer::GetInstance);
具体的实例化函数如下,同样是先得到初始化算子需要的参数params,这些参数的初始化过程和池化算子的初始化过程类似。
ParseParameterAttrStatus ConvolutionLayer::GetInstance(
const std::shared_ptr<RuntimeOperator>& op,
std::shared_ptr<Layer>& conv_layer)
然后根据以上的得到的参数对卷积算子进行初始化,但是在这里,还没有对卷积算子中的权重(weight和bias)进行加载。
conv_layer = std::make_shared<ConvolutionLayer>(
out_channel->value, in_channel->value, kernels.at(0), kernels.at(1),
paddings.at(0), paddings.at(1), strides.at(0), strides.at(1),
groups->value, use_bias->value);
卷积算子中的权重和偏移量初始化、加载过程:
const std::map<std::string, std::shared_ptr<RuntimeAttribute>>& attrs =
op->attribute;
...
const auto& bias = attrs.at("bias");
const std::vector<int>& bias_shape = bias->shape;
if (bias_shape.empty() || bias_shape.at(0) != out_channel->value) {
LOG(ERROR) << "The attribute of bias shape is wrong";
return ParseParameterAttrStatus::kAttrMissingBias;
}
const std::vector<float>& bias_values = bias->get<float>();
conv_layer->set_bias(bias_values);
}
首先获取到了RuntimeOperator中的权重变量attrs。然后找到其中的bias键。如果该键存在,就获取其中的偏移量权重(bias),并将其赋值给conv_layer。
const auto& weight = attrs.at("weight");
const std::vector<int>& weight_shape = weight->shape;
if (weight_shape.empty()) {
LOG(ERROR) << "The attribute of weight shape is wrong";
return ParseParameterAttrStatus::kAttrMissingWeight;
}
const std::vector<float>& weight_values = weight->get<float>();
conv_layer->set_weights(weight_values);
auto conv_layer_derived =
std::dynamic_pointer_cast<ConvolutionLayer>(conv_layer);
CHECK(conv_layer_derived != nullptr);
conv_layer_derived->InitIm2ColWeight();
return ParseParameterAttrStatus::kParameterAttrParseSuccess;
同样的,获取RuntimeOperator中的weight键,如果该键存在,就获取其对应的权重变量,并将它赋值给conv_layer。 至此,完成了卷积算子的实例化。可以看到,这里有一个InitIm2ColWeight函数,它是在展开该卷积算子对应的卷积核。对于一个卷积算子来说,它的输入是不确定的,所以需要在运行时再调用Im2Col进行展开,而一个卷积算子中的权重是固定的,所以可以在初始化的时候进行展开。
