当前位置： 首页 > article >正文

贝塞尔曲线

article 2024/11/14 9:30:42

QPainterPath 可以用来画贝塞尔曲线，什么是贝塞尔曲线呢？开始学的时候，经常听到贝塞尔曲线，但一直不知道是什么东西，很神秘的样子，据说很复杂，一直没敢学，人类对陌生的东西总是有恐惧感，这一部分就来揭开贝塞尔曲线神秘的面纱（大部分内容都来自于网络）。

贝塞尔曲线（The Bézier Curves），是一种在计算机图形学中相当重要的参数曲线（3D的称为曲面）。贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所发表，他运用贝塞尔曲线来为汽车的主体进行设计。

一般的矢量图形软件通过它来精确画出曲线，贝塞尔曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。

贝塞尔曲线还是很抽象的，如果不是看了下面的这些动态图，演示了贝塞尔曲线的生成过程，估计仍然很难明白贝塞尔曲线是什么样的，控制点是什么，有什么用。

塞尔曲线的通用公式为：

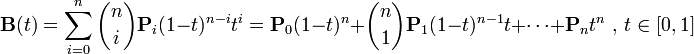
看上去是不是很复杂，难以理解？谁都一样，开始时看到这么复杂的公式，都会头大，但是看完下面的一阶，二阶，三阶贝塞尔曲线的方程和生成动画后就明白了，原来大名鼎鼎的贝塞尔曲线也不难嘛。

一阶贝塞尔曲线 就是线段，没有控制点，其参数方程为
 


下图是生成一阶贝塞尔曲线的动画：

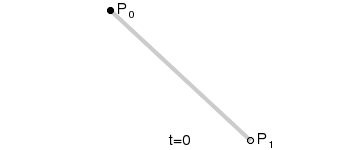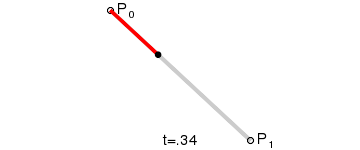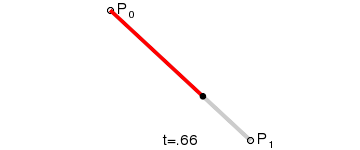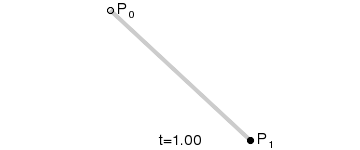
二阶贝塞尔曲线 只有一个控制点，为 P1，其参数方程为
 


下图是生成二阶贝塞尔曲线的动画：

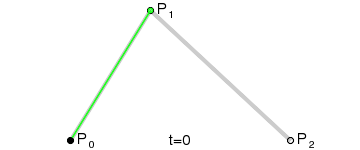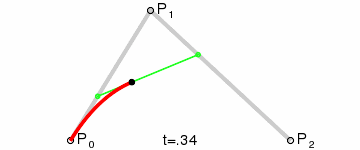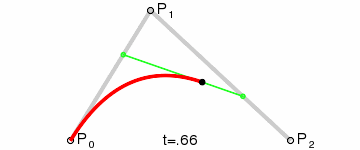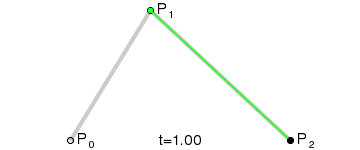
把其中的任意一帧拿出来分析，可以看到 MP0/MP1，NP1/Np2，KM/KN 都为 t/(1-t)，是不是一下又明白了很多，其他阶的贝塞尔曲线也是这样的。

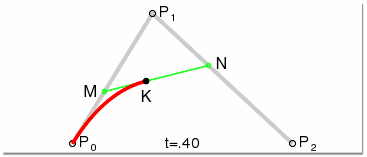
三阶贝塞尔曲线 有两个控制点，为 P1, P2，其参数方程为
 


下图是生成三阶贝塞尔曲线的动画：

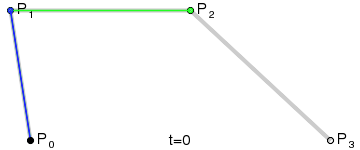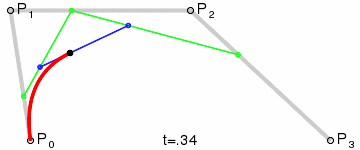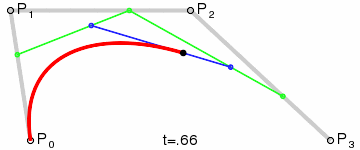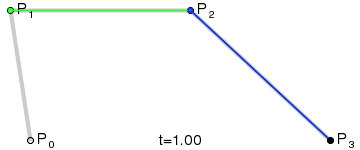
贝塞尔曲线的更多介绍和动画请参考 http://bbs.csdn.net/topics/390358020。

绘制二阶贝塞尔曲线使用 quadTo()，第一个参数是控制点，第二个参数是曲线的终点

1

void QPainterPath::quadTo(const QPointF &c, const QPointF &endPoint)

绘制三阶贝塞尔曲线使用 cubicTo()，第一个和第二个参数是控制点，第三个参数是曲线的终点

1

void QPainterPath::cubicTo(const QPointF &c1, const QPointF &c2, const QPointF &endPoint)

或许你会问：为什么只看到了控制点和终点，没有看到起点？这是因为 QPainterPath 默认的起点在 (0, 0)，可以使用 moveTo() 改变起点，前一条线的终点就是下一条线的起点，结束亦是开始，人生亦是如此，生活处处皆道理，留心处处是学问，一花一世界，一叶一菩提，编程亦能悟道。

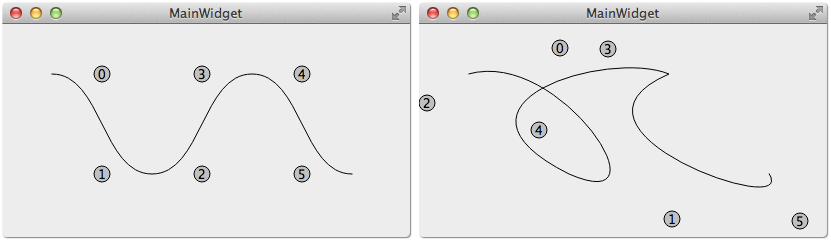
这里演示一个小程序，QPainterPath 添加了三条贝塞尔曲线，每条曲线有两个控制点，如图显示的 0 到 5 个共 6 个控制点，拖动控制点就会改变它的坐标，然后生成新的贝塞尔曲线并显示出来，实时的看到变化的结果。通过拖动控制点，可以生成各种不同的平滑曲线，这就是贝塞尔曲线的魅力所在。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

// 文件名：BezierCurveWidget.h
#ifndef BEZIERCURVEWIDGET_H
#define BEZIERCURVEWIDGET_H

#include <QWidget>
#include <QPointF>
#include <QList>
#include <QPainterPath>

class BezierCurveWidget : public QWidget {
    Q_OBJECT

public:
    explicit BezierCurveWidget(QWidget *parent = 0);
    ~BezierCurveWidget();

protected:
    void mousePressEvent(QMouseEvent *event) Q_DECL_OVERRIDE;
    void mouseMoveEvent(QMouseEvent *event) Q_DECL_OVERRIDE;
    void paintEvent(QPaintEvent *event) Q_DECL_OVERRIDE;

    /**
     * 使用 breakPoints 和 controlPoints 创建贝塞尔曲线
     * 当控制点的坐标变化后都重新生成一次贝塞尔曲线
     */
    QPainterPath createBezierCurve();

    /**
     * 创建显示控制点的圆的 bounding rectangle
     * @param index 控制点在 controlPoints 中的下标
     */
    QRect createControlPointBundingRect(int index);

    /**
     * 为了设置坐标方便，从 (0, 0) 开始设置而不是实际绘制的坐标，对绘制贝塞尔曲线和控制点的
     * 坐标系做了偏移，在计算的时候，坐标也要是相对于新坐标系的坐标才行，不能是原始的坐标，
     * 所以要对其也好做相应的偏移
     * @param point - 例如鼠标按下时在 widget 上的原始坐标
     */
    QPointF translatedPoint(const QPointF &point) const;

private:
    QPainterPath bezierCurve;       // 贝塞尔曲线
    QList<QPointF *> breakPoints;   // 贝塞尔曲线端点的坐标
    QList<QPointF *> controlPoints; // 贝塞尔曲线控制点的坐标
    int pressedControlPointIndex;   // 鼠标按住的控制点在 controlPoints 里的下标
    int controlPointRadius;         // 显示控制点的圆的半径

    int translatedX; // 坐标系 X 轴的偏移量
    int translatedY; // 坐标系 Y 轴的偏移量
    int flags;       // 文本显示的参数
};

#endif // BEZIERCURVEWIDGET_H


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

// 文件名：BezierCurveWidget.cpp
#include "BezierCurveWidget.h"
#include <QPainter>
#include <QMouseEvent>

BezierCurveWidget::BezierCurveWidget(QWidget *parent) : QWidget(parent) {
    // 贝塞尔曲线的端点
    breakPoints.append(new QPointF(0, 0));
    breakPoints.append(new QPointF(100, 100));
    breakPoints.append(new QPointF(200, 0));
    breakPoints.append(new QPointF(300, 100));

    // 第一段贝塞尔曲线控制点
    controlPoints.append(new QPointF(50, 0));
    controlPoints.append(new QPointF(50, 100));

    // 第二段贝塞尔曲线控制点
    controlPoints.append(new QPointF(150, 100));
    controlPoints.append(new QPointF(150, 0));

    // 第三段贝塞尔曲线控制点
    controlPoints.append(new QPointF(250, 0));
    controlPoints.append(new QPointF(250, 100));

    // 坐标设置好后就可以生成贝塞尔曲线了
    bezierCurve = createBezierCurve();

    controlPointRadius = 8;
    translatedX = 50;
    translatedY = 50;
    flags = Qt::AlignHCenter | Qt::AlignVCenter; // 水平和垂直居中
}

BezierCurveWidget::~BezierCurveWidget() {
    qDeleteAll(breakPoints);
    qDeleteAll(controlPoints);
}

void BezierCurveWidget::mousePressEvent(QMouseEvent *event) {
    pressedControlPointIndex = -1;

    // 绘制贝塞尔曲线和控制点的坐标系做了偏移，鼠标按下的坐标也要相应的偏移
    QPointF p = translatedPoint(event->pos());

    // 鼠标按下时，选择被按住的控制点
    for (int i = 0; i < controlPoints.size(); ++i) {
        QPainterPath path;
        path.addEllipse(*controlPoints.at(i), controlPointRadius, controlPointRadius);

        if (path.contains(p)) {
            pressedControlPointIndex = i;
            break;
        }
    }
}

void BezierCurveWidget::mouseMoveEvent(QMouseEvent *event) {
    // 移动选中的控制点
    if (pressedControlPointIndex != -1) {
        QPointF p = translatedPoint(event->pos());
        controlPoints.at(pressedControlPointIndex)->setX(p.x());
        controlPoints.at(pressedControlPointIndex)->setY(p.y());
        bezierCurve = createBezierCurve(); // 坐标发生变化后重新生成贝塞尔曲线
        update(); // 刷新界面
    }
}

QPainterPath BezierCurveWidget::createBezierCurve() {
    QPainterPath curve;
    curve.moveTo(*breakPoints.at(0));
    curve.cubicTo(*controlPoints[0], *controlPoints[1], *breakPoints[1]);
    curve.cubicTo(*controlPoints[2], *controlPoints[3], *breakPoints[2]);
    curve.cubicTo(*controlPoints[4], *controlPoints[5], *breakPoints[3]);

    return curve;
}

QRect BezierCurveWidget::createControlPointBundingRect(int index) {
    int x = controlPoints.at(index)->x() - controlPointRadius;
    int y = controlPoints.at(index)->y() - controlPointRadius;

    return QRect(x, y, controlPointRadius * 2, controlPointRadius * 2);
}

QPointF BezierCurveWidget::translatedPoint(const QPointF &point) const {
    return point - QPointF(translatedX, translatedY);
}

void BezierCurveWidget::paintEvent(QPaintEvent *) {
    QPainter painter(this);
    painter.setRenderHint(QPainter::Antialiasing);
    painter.translate(translatedX, translatedY);

    // 绘制贝塞尔曲线
    painter.drawPath(bezierCurve);

    // 绘制控制点和控制点的序号
    painter.setBrush(Qt::lightGray);
    for (int i = 0; i < controlPoints.size(); ++i) {
        QRect rect = createControlPointBundingRect(i);
        painter.drawEllipse(rect);
        painter.drawText(rect, flags, QString("%1").arg(i));
    }
}

1
2
3
4
5
6
7
8
9
10

// 文件名：main.cpp
#include "BezierCurveWidget.h"
#include <QApplication>

int main(int argc, char *argv[]) {
    QApplication a(argc, argv);
    BezierCurveWidget w;
    w.show();
    return a.exec();
}

这个程序不能像拖动控制点那样拖动曲线的端点改变贝塞尔曲线，这就作为留给大家的作业吧。


http://www.kler.cn/a/283147.html

相关文章：

  • FatLab：我的编程课程系列
  • 【日志】392.判断子序列
  • 软件测试面试八股文（超详细整理）
  • 单元测试、集成测试、系统测试有什么区别
  • nginx部署H5端程序与PC端进行区分及代理多个项目及H5内页面刷新出现404问题。
  • 【网络工程】计算机硬件概述
  • uniapp小程序怎么判断滑动的方向
  • Redis—基础篇
  • 如何让大模型学会自我反思
  • VMware安装Ubuntu 23.10.1系统图文版
  • Yolo环境搭建（深度学习基础环境）
  • 在Docker中，本地的镜像文件都存放在哪里？
  • 数据安全守护者：精通数据备份与恢复的艺术
  • 优化大型语言模型微调：MoLA层级专家分配策略
  • CSS3 3D 转换
  • HarmonyOS鸿蒙开发（ Beta5版）Navigation组件常规加载与动态加载
  • Ubuntu 20.04 源码编译安装OpenCV 4.5.0
  • C++：继承用法详解~
  • 从挫败到精通：三步克服编程学习的难关
  • 【Leetcode 2206 】 将数组划分成相等数对 —— 哈希表与数组模拟哈希表
  • Elasticsearch 中，term 查询和 match 查询的区别
  • JavaScript常见知识点总结
  • 搜维尔科技：‌XSENS高精度惯性动作捕捉系统，人形机器人Al训练专用设备
  • 华为HCIP-datacom 真题 (2024年下半年最新题库)
  • Vue + Spring Boot + SQL Server + Python 部署到 Windows 服务器
  • 最长公共子序列