第七讲 贪心
文章目录
- 股票买卖 II
- 货仓选址(贪心:排序+中位数)
- 糖果传递(❗·贪心:中位数)
- 雷达设备(贪心+排序)
- 付账问题(平均值+排序❓)
- 乘积最大(排序/双指针)
- 后缀表达式(👍绝对值/分类讨论/贪心)
股票买卖 II

思路:只要对于今天来说明天的价格比今天高,我们就买,明天卖了肯定会获利。
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = (int) (1e5 + 10);
static int[] a = new int[N];
static long ans = 0;
public static void main(String[] args) throws Exception{
int n = sc.nextInt();
for(int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
}
for(int i = 2; i <= n; i++) {
if(a[i] > a[i - 1]) {
ans += (a[i] - a[i - 1]);
}
}
System.out.println(ans);
}
}
货仓选址(贪心:排序+中位数)
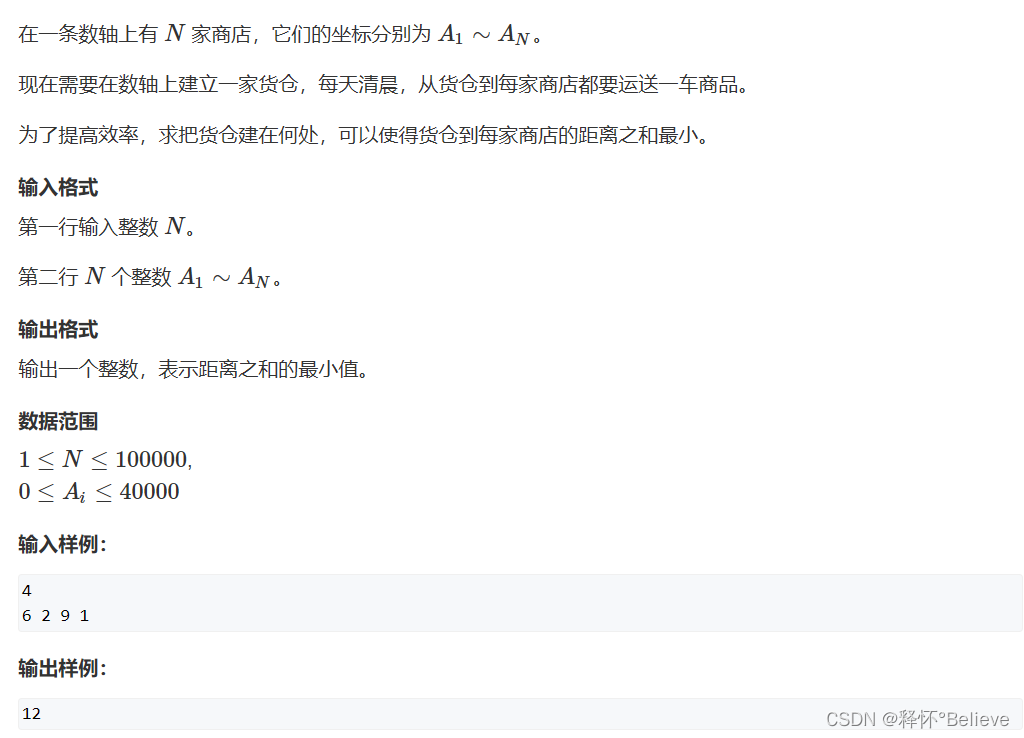
选中位数对两边来说都比较优
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = (int) (1e5 + 10);
static int[] a = new int[N];
static long ans = 0;
public static void main(String[] args) throws Exception{
int n = sc.nextInt();
for(int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
}
Arrays.sort(a,1, 1 + n);
int mid = (n + 1)/2;
for(int i = 1; i <= n; i++) {
ans = ans + Math.abs(a[i] - a[mid]);
}
System.out.println(ans);
}
}
糖果传递(❗·贪心:中位数)
本人还不是太明白
雷达设备(贪心+排序)
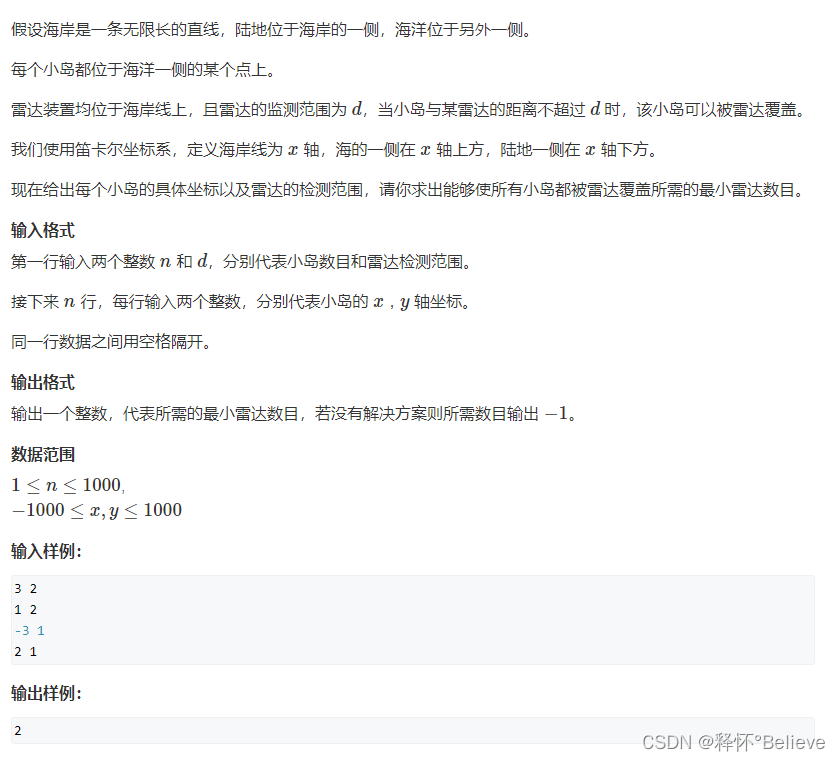
这道题也不太会,太菜了,😢
看的别人的题解,很妙题解
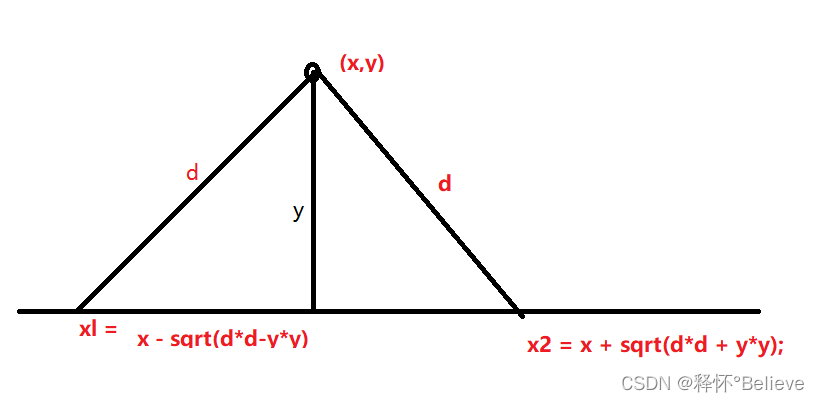
首先我们需要将小岛的坐标转换为区间,x只有在[x1,x2]才可以被搜到。
转换为以后就变成了区间覆盖问题 ,但是我们需要对区间从小到达(右端点)从小到大排序,我们只需要哦使用最近的雷达去判断是否可以,如果不可以就需要在加一个。
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = (int) (1e4 + 10);
static node[] a = new node[N];
static int ans = 0;
static int n = 0,d = 0;
static boolean[] vis = new boolean[N];
public static void main(String[] args) throws Exception{
n = sc.nextInt();
d = sc.nextInt();
for(int i = 1; i <= n; i++) {
int x,y;
x = sc.nextInt();
y = sc.nextInt();
y = Math.abs(y);
if(y > d) {
System.out.println(-1);
return;
}
a[i] = new node();
a[i].l = x - Math.sqrt(d*d-y*y);
a[i].r = x + Math.sqrt(d*d-y*y);
}
Arrays.sort(a,1,1 + n,new cmp());
// for(int i = 1; i <= n; i++) {
// System.out.println(a[i].r);
// }
for(int i = 1;i <= n; i++) {
if(!vis[i]) {
ans++;
vis[i] = true;
for(int j = i + 1; j <= n; j++) {
if(a[j].l <= a[i].r) {
vis[j] = true;
}
}
}
}
System.out.println(ans);
}
}
class node{
double l,r;
}
class cmp implements Comparator<node>{
public int compare(node o1, node o2) {
if(o1.r < o2.r) {
return -1;
}else {
return 1;
}
}
}
付账问题(平均值+排序❓)

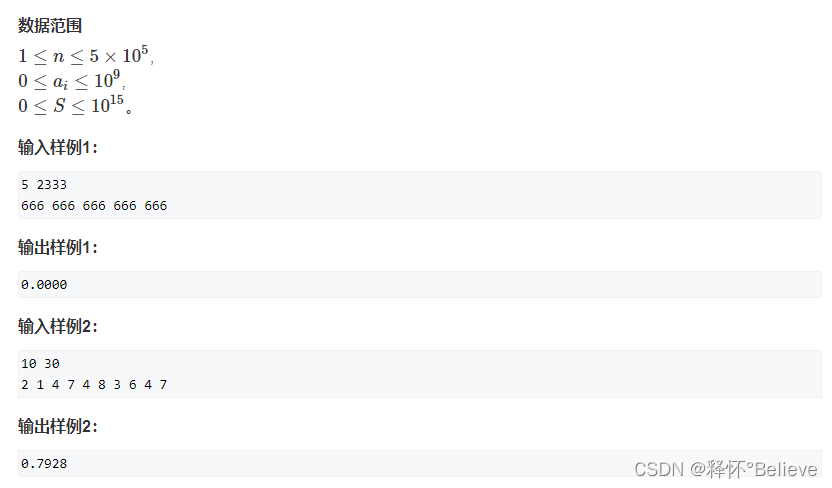
思路:显然是所有人付的钱越接近平均数标准差越小,我们让所有人的数据尽可能接近标准差,首先算出平均值,然后将其进行排序,低于平均值的人把所有钱都拿出来,其余的由其他人平摊(需要注意精度问题,竟然还要用long double)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 500010;
int n;
int a[N];
int main()
{
long double s;
cin >> n >> s;
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
long double res = 0, avg = s / n;
for (int i = 0; i < n; i ++ )
{
double cur = s / (n - i);//当前需要交多少钱
if (a[i] < cur) cur = a[i];//如果当前的钱不够,那么就全部交
res += (cur - avg) * (cur - avg); //把平方加到答案里面
s -= cur;//剩下需要交的钱就减少了cur
}
printf("%.4Lf\n", sqrt(res / n));
return 0;
}
乘积最大(排序/双指针)

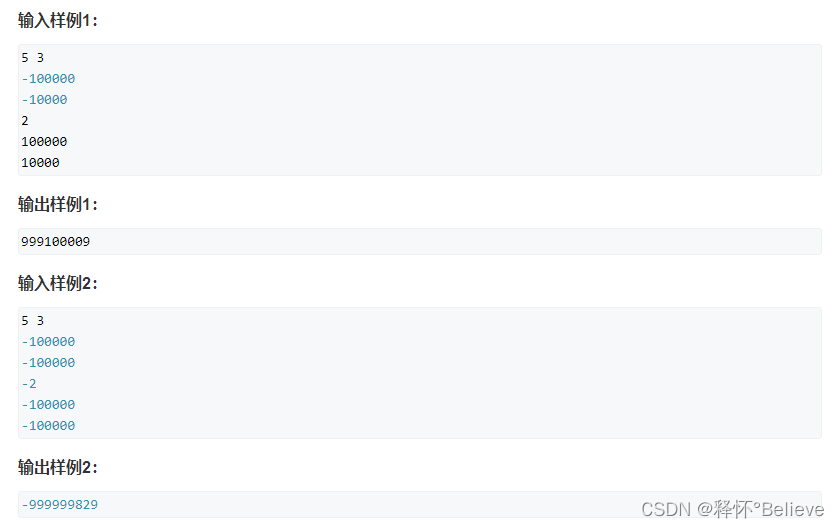
思路:对于k是奇数且k<n的情况,我们需要特殊处理一下,转换为普遍情况,我们取一个最大的数,此时k就转换为偶数,我们可以使用双指针算法,首先对所有数进行排序,很显然负数绝对值大的在左边,偶数绝对值大的在右边,如果必须选一个正的一个负的话,显然是选的负数绝对值较小的与正数数值较小的,加个负号,显然是比较小的。
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 100010;
static int ans = 0;
static int n = 0,k = 0;
static int[]a = new int[N];
static int mod = 1000000009;
public static void main(String[] args) throws Exception{
n = sc.nextInt();
k = sc.nextInt();
for(int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
}
Arrays.sort(a,1,1 +n);
long res = 1;//初始化乘积
int l = 1, r = n;
int sign = 1;//标记符号位
if(k % 2 == 1) {
res = a[r--];//选取最大的一个数
if(res < 0) {
sign = -1;
}
k--;
}
while(k > 0) {
long x = (long)a[l] * a[l+1];
long y = (long)a[r] * a[r-1];
if(x * sign > y * sign) {
res = ((res % mod) * (x % mod));//不太懂为啥
l += 2;
}else {
res = ((y % mod) * (res % mod));
r -= 2;
}
k-=2;
}
System.out.println(res%mod);
}
// static int md(int x) {
// if(x > 0) {
// return x%mod;
// }else {
//
// }
// }
}
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 100010;
static int ans = 0;
static int n = 0,k = 0;
static int[]a = new int[N];
static int mod = 1000000009;
public static void main(String[] args) throws Exception{
n = sc.nextInt();
k = sc.nextInt();
for(int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
}
Arrays.sort(a,1,1 +n);
long res = 1;//初始化乘积
int l = 1, r = n;
int sign = 1;//标记符号位
if(k % 2 == 1) {
res = a[r--];//选取最大的一个数
if(res < 0) {
sign = -1;
}
k--;
}
while(k > 0) {
long x = (long)a[l] * a[l+1];
long y = (long)a[r] * a[r-1];
if(x * sign > y * sign) {
res = (md(x) * md(res));//不太懂为啥
l += 2;
}else {
res = (md(y) * md(res));
r -= 2;
}
k-=2;
}
System.out.println(md(res));
}
static long md(long x) {
if(x > 0) {
return x % mod;
}else {
return 0-((0-x)%(long)1000000009);
}
}
}
是否判断正负都是可以的,不太懂
后缀表达式(👍绝对值/分类讨论/贪心)

中缀表达式:运算符在两个操作数的位置
后缀表达式:运算符在两个操作数的后面
前缀表达式:运算符在两个操作数的前面
其实感觉和后缀表达式没有太大的关系,即使不懂也可以做
显然我们需要谈论:
(1)最简单的一种就是全是➕号,此时我们不需要进行什么操作,显然答案就是所有数的和。
(2)有一个➖号,此时我们可以通过不同的加减号的位置,可以是➕号也发挥减号的作用,-(+…+…)=>(-…-…),此时等价于好多➖号
(3)存在多个➖号,此时减号既可以当➕号,也可以当➖,因为-(-x) = +x,此时我们需要讨论所给数的正负,
对于全为加号的我们不在讨论,
如果存在减号,
1)如果全是正数,那么至少会有一个数会被减掉
2)如果全是负数,我们需要找一个最大的负数,其他的全变正数,比如-2,-3,-4,-5和3个减号,我们可以变为-2-(-5)-(-4)-(-3)此时显然是最大的。
3)有正有负,所有正数匹配正号,所有负数匹配负号,最终就是所有数的绝对值之和,比如1,2,(-3)转换为,2个➖号:1-(-3-2)=6,2-(-3-1)=6
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;
import java.util.Scanner;
public class Main{
static Scanner sc = new Scanner(System.in);
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 1000100;
static long ans = 0;
static int n = 0,m = 0;
static int[]a = new int[N];
public static void main(String[] args) throws Exception{
n = sc.nextInt();
m = sc.nextInt();
int k = n + m + 1;
for(int i = 1; i <= k; i++) {
a[i] = sc.nextInt();
ans = ans + (long)a[i];
}
if(m == 0) {
System.out.println(ans);
}else {
Arrays.sort(a,1,1+k);
ans = 0;
ans = a[k] - a[1];
// System.out.println(ans);
for(int i = 2; i < k; i++) {
ans = ans + (long)Math.abs(a[i]);
}
System.out.println(ans);
}
}
}
