CS224W—07 Machine Learning with Heterogeneous Graphs

CS224W—07 Machine Learning with Heterogeneous Graphs

本节中，我们将学习如何在异构图中进行图神经网络学习。

Heterogeneous Graphs

图中的节点类型/边类型不同，就会形成一个异构图（Heterogeneous Graph），例如下图中的节点有两种类型：Paper节点/Author节点；第二个图中的边有两种类型：Cite/Like；也可以是多种节点和边的结合，如第三个图。

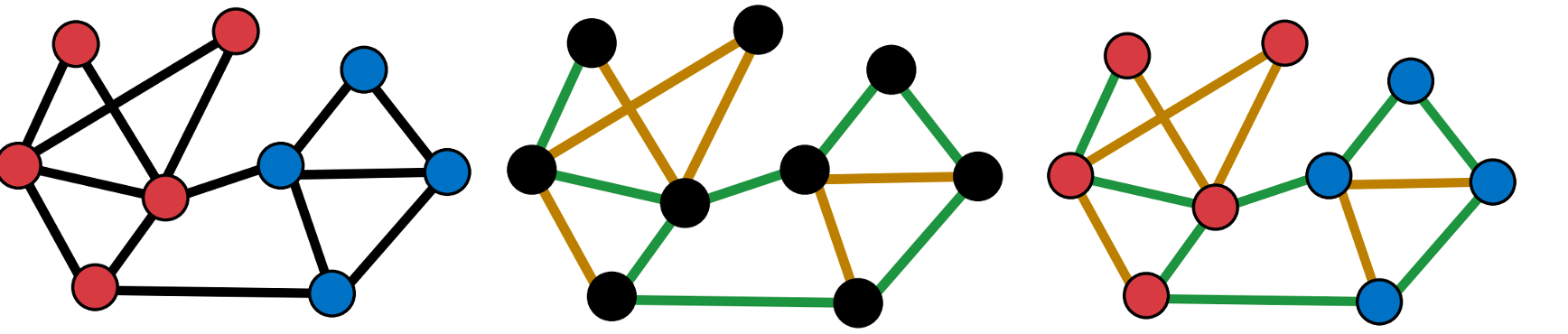
为了更好的捕捉节点和边的交互，使用relation type来描述一条边：

Relation Type: (node_start, edge, node_end)

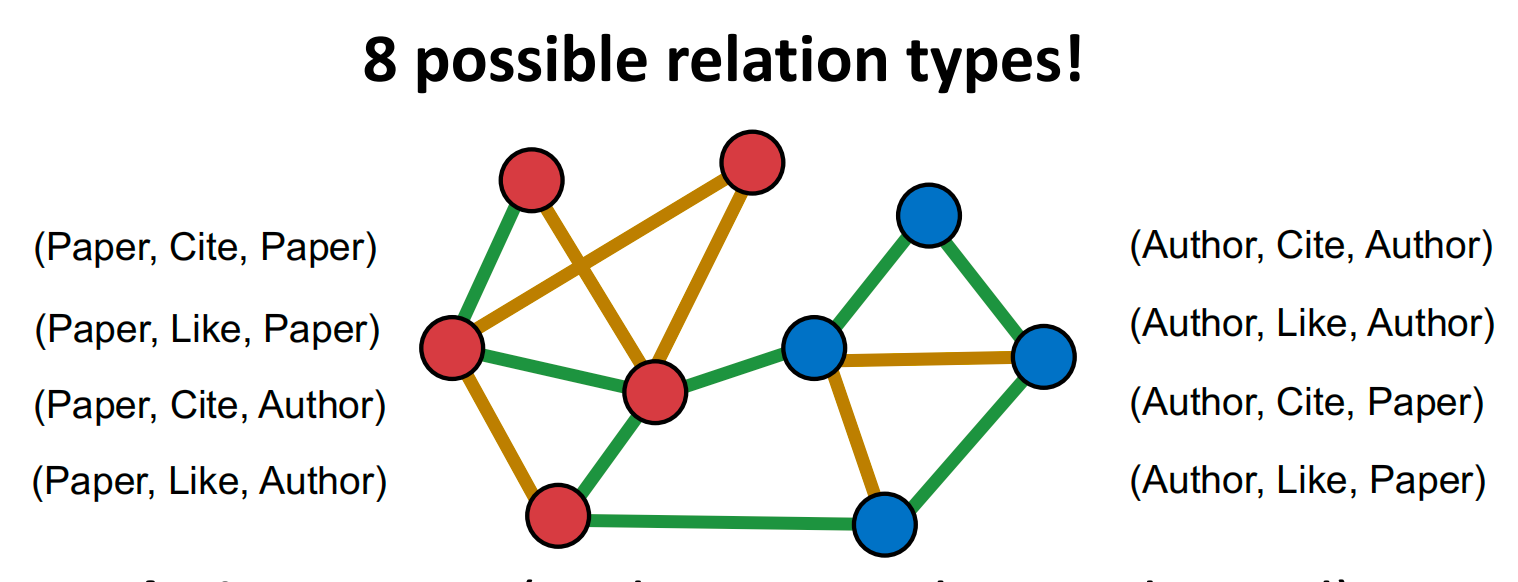
异构图定义为
$$G=(V,E,\tau ,\varphi )$$

• 具有节点类型 $\tau (v)$ 的节点 $v\in V$

• 具有边类型 $\varphi (u,v)$ 的边 $(u,v)\in E$

• 边 $e$ 的relation type是一个元组：$r(u,v)=\left(\tau (u),\varphi (u,v),\tau (v)\right)$

观察：我们也可以将节点和边的类型视为特征 示例：为节点和边添加一位有效指示器

• 给每个“作者节点”附加特征 [1, 0]；
• 给每个“论文节点”附加特征 [0, 1]
• 同样，我们可以为不同类型的边分配边特征；然后，异构图简化为标准图

那我们何时需要异构图？

• 情景1:不同的节点/边类型有不同形状的特征
• 情景2:不同的relation type代表不同类型的interaction
  • 比如 (English, translate, French) 和 (English, translate, Chinese) 需要不同的模型。

异构图的计算成本是很高的，也有许多方法将异构图转换为同构图来进行计算。

Relational GCN (RGCN)

论文地址：https://arxiv.org/pdf/1703.06103

经典的GCN：

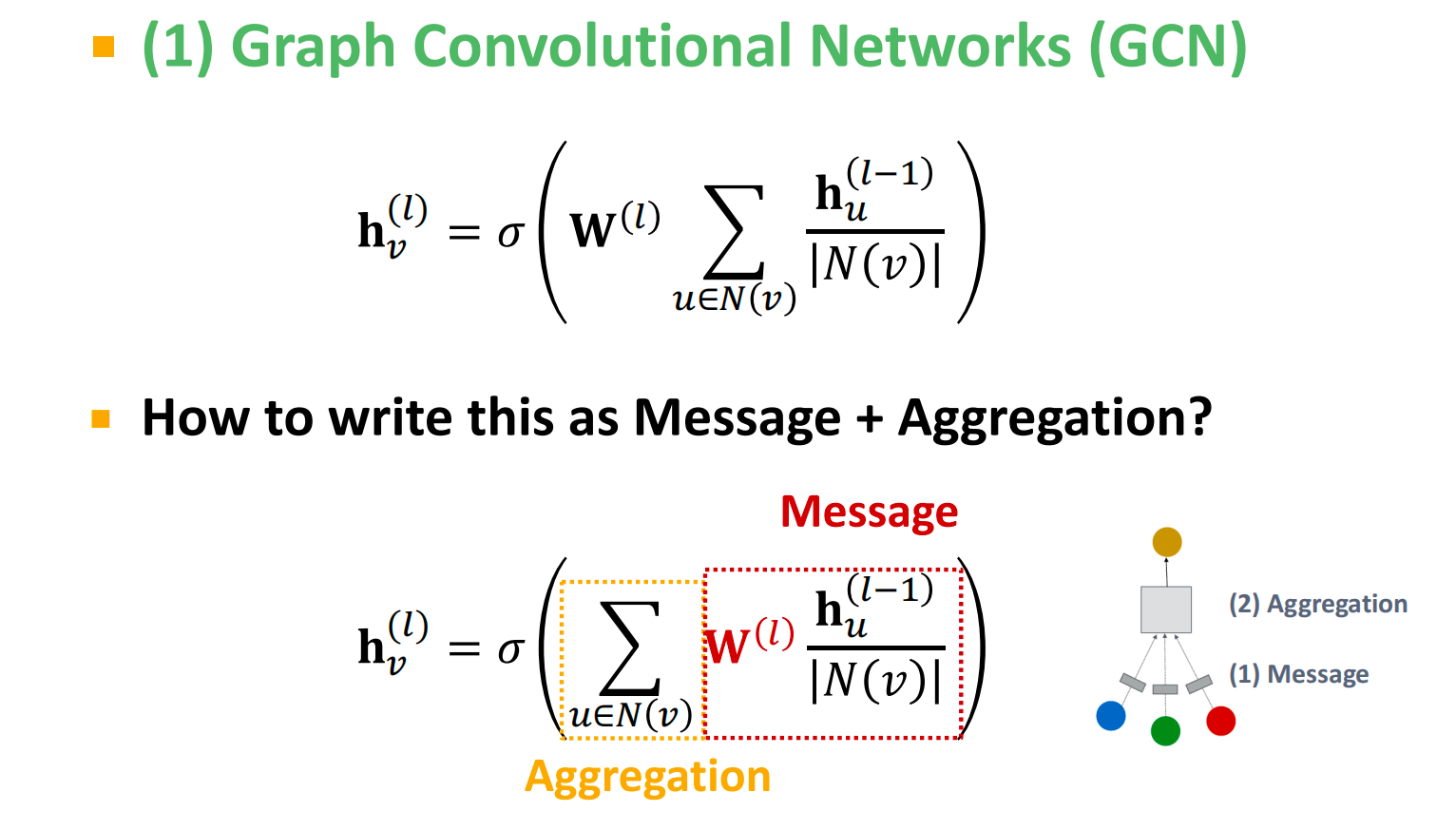
对于只有一种relation的有向图：

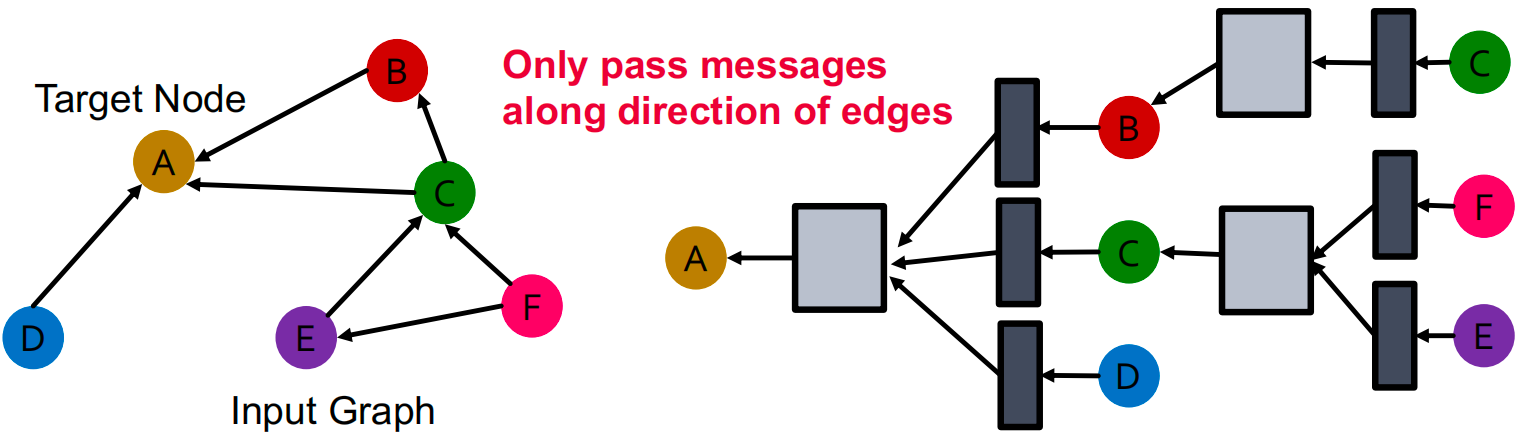
对于有多种relation types的图，不同的relation type 使用不同的神经网络参数：

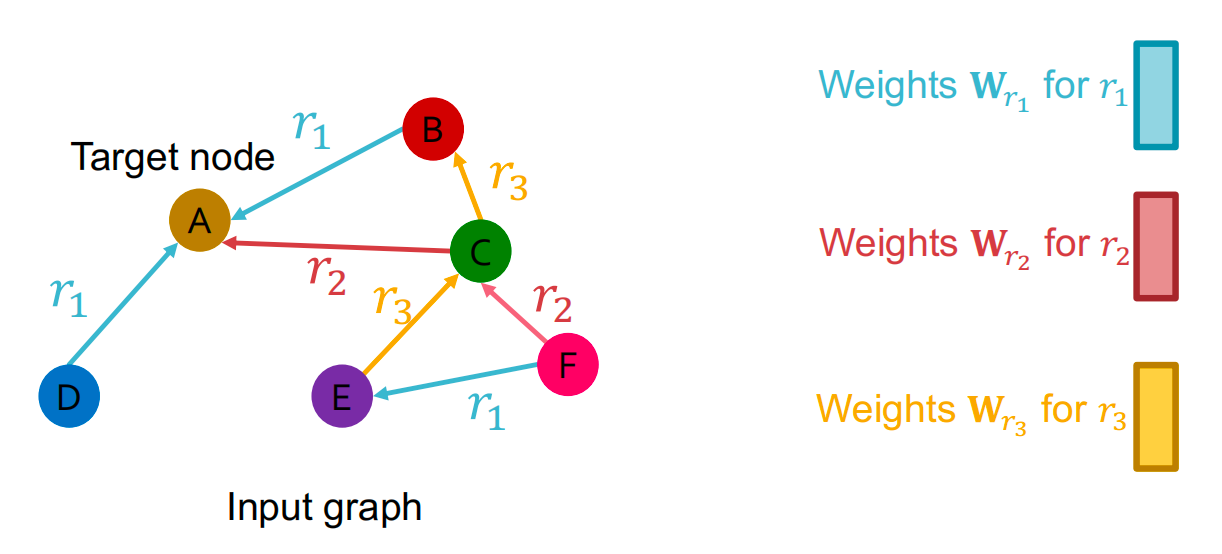
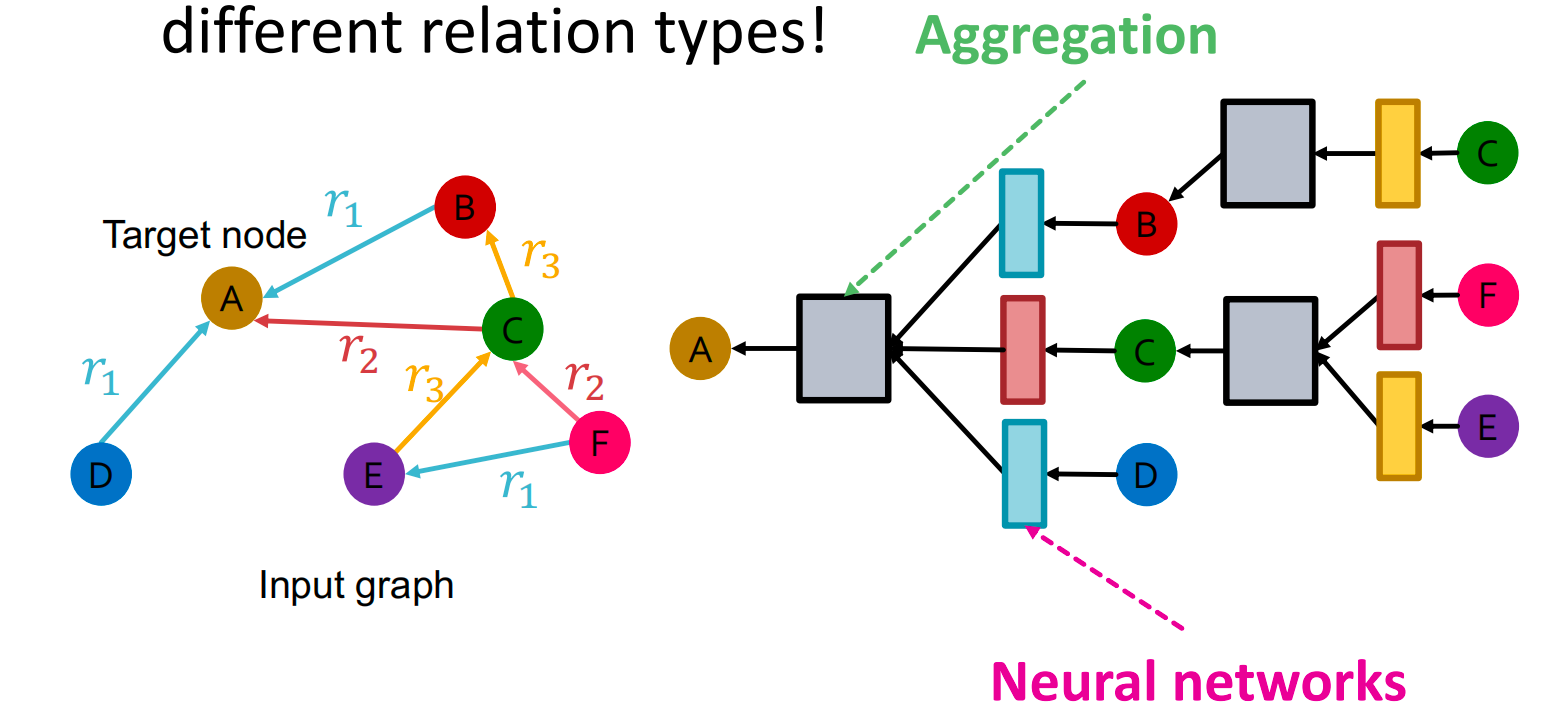
RGCN Definition

$${\mathbf{h}}_v^{(l+1)}=\sigma \left(\sum _{r\in R}\sum _{u\in N_v^r}\frac{1}{C_{\nu ,r}}{\mathbf{W}}_r^{(l)}{\mathbf{h}}_u^{(l)}+{\mathbf{W}}_0^{(l)}{\mathbf{h}}_v^{(l)}\right)$$

Message：

• 每个给定relation ( r ) 的领居消息：
  $${\mathbf{m}}_{u,r}^{(l)}=\frac{1}{c_{v,r}}{\mathbf{W}}_r^{(l)}{\mathbf{h}}_u^{(l)},c_{v,r}=|N_v^r|$$

• 自身消息：
  $${\mathbf{m}}_v^{(l)}={\mathbf{W}}_0^{(l)}{\mathbf{h}}_v^{(l)}$$

Aggregation:

• 对来自邻居和自身的消息进行求和，然后进行激活：
  $${\mathbf{h}}_v^{(l+1)}=\sigma \left(\mathrm{Sum}\left(\left\{{\mathbf{m}}_{u,r}^{(l)},u\in N(v)\right\}\cup \left\{{\mathbf{m}}_v^{(l)}\right\}\right)\right)$$

RGCN Scalability

每种关系都有 $L$ 个矩阵：$W_r^{(1)},W_r^{(2)}\cdots W_r^{(L)}$。每个 $W_r^{(l)}$ 的大小是 $d^{(l+1)}\times d^{(l)}$，$d^{(l)}$ 是第 $l$ 层的隐藏维度。

参数数量相对于关系数量的快速增长！过拟合成为一个问题。

两种方法来正则化权重 $W_r^{(l)}$：

1. 使用分块对角矩阵（ Block Diagonal Matrices）
2. 基/字典学习（Basis/Dictionary learning）

Block Diagonal Matrices

关键：使权重变得稀疏！使用分块对角矩阵对 $W_r$ 进行稀疏化

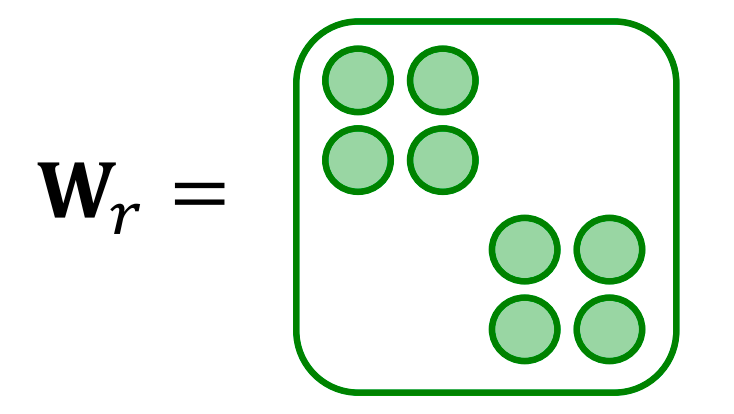
限制：只有邻近的神经元/维度可以通过 $W$ 进行交互。 如果使用 $B$ 个低维矩阵，则参数数量从 $d^{(l+1)}\times d^{(l)}$ 减少到 $B\times \frac{d^{(l+1)}}{B}\times \frac{d^{(l)}}{B}$。

Basis Learning

关键：在不同的relation之间分享权重

将每种关系的矩阵表示为基变换的线性组合：
$$W_r=\sum _{b=1}^B{a}_{rb}\cdot V_b,$$
其中 $V_b$ 在所有关系中共享。

1. $V_b$ 是基矩阵。

2. $a_{rb}$ 是矩阵 $V_b$ 的重要性权重。

现在每种关系只需要学习 { a r b } b = 1 B \{a_{r b}\}_{b=1}^{B} {arb​}b=1B​，这是 $B$ 个标量。

Example: Entity/Node Classification

任务：对于给定节点，预测其标签

如果我们从 $k$ 个类别中预测节点 A 的类别，取最后一层（预测头）：$h_A^{(L)}\in {\mathbb{R}}^k$，$h_A^{(L)}$ 中的每个项代表该类别的概率。

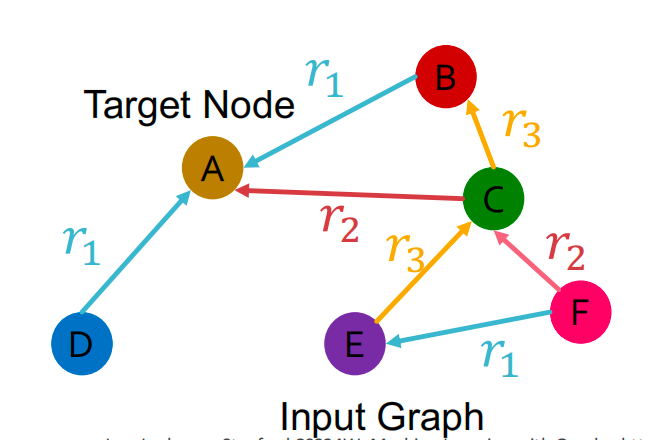
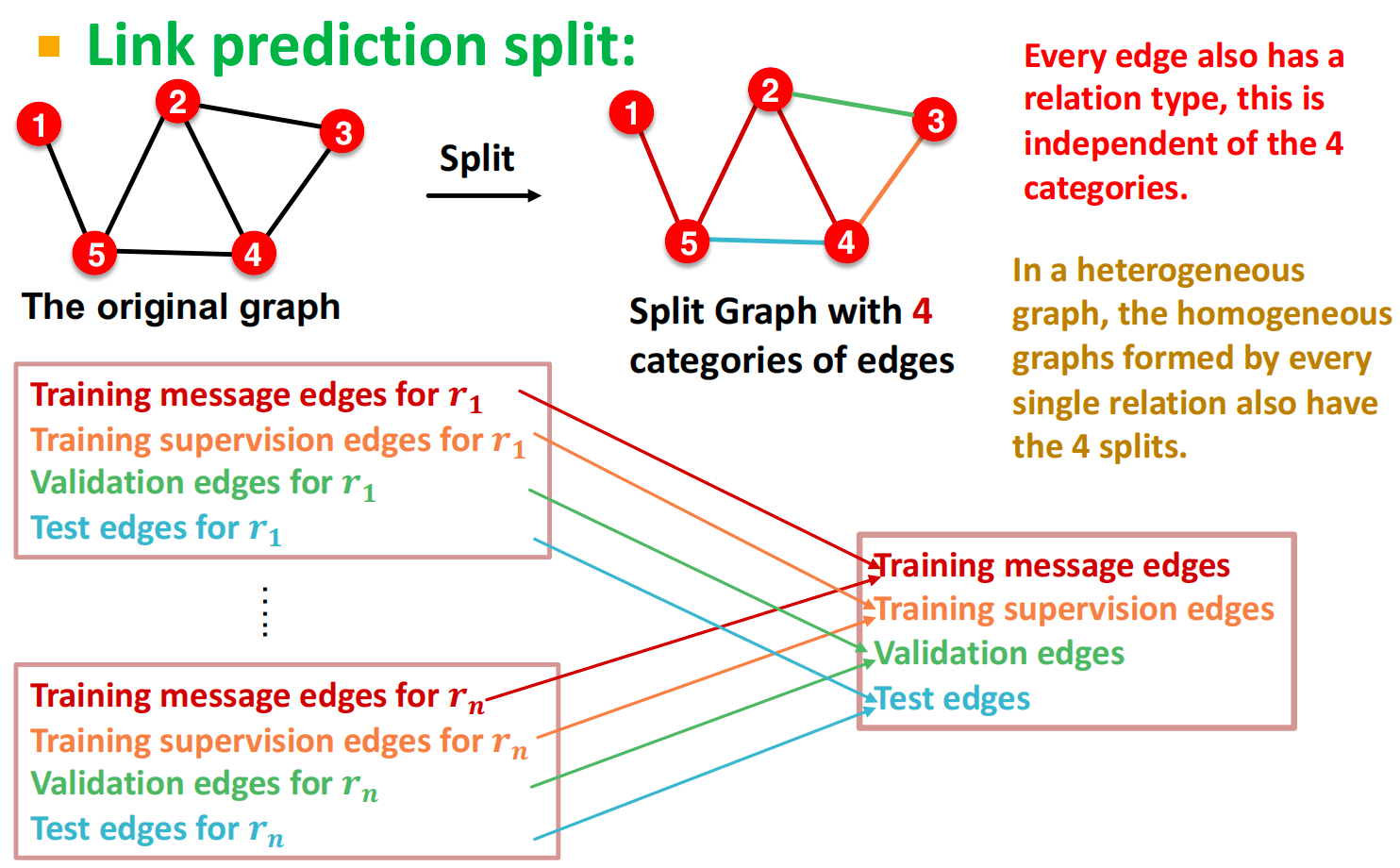
Link Prediction

在异质图中，将每种关系对应的边都分成 training message edges, training supervision edges, validation edges, test edges 四类。

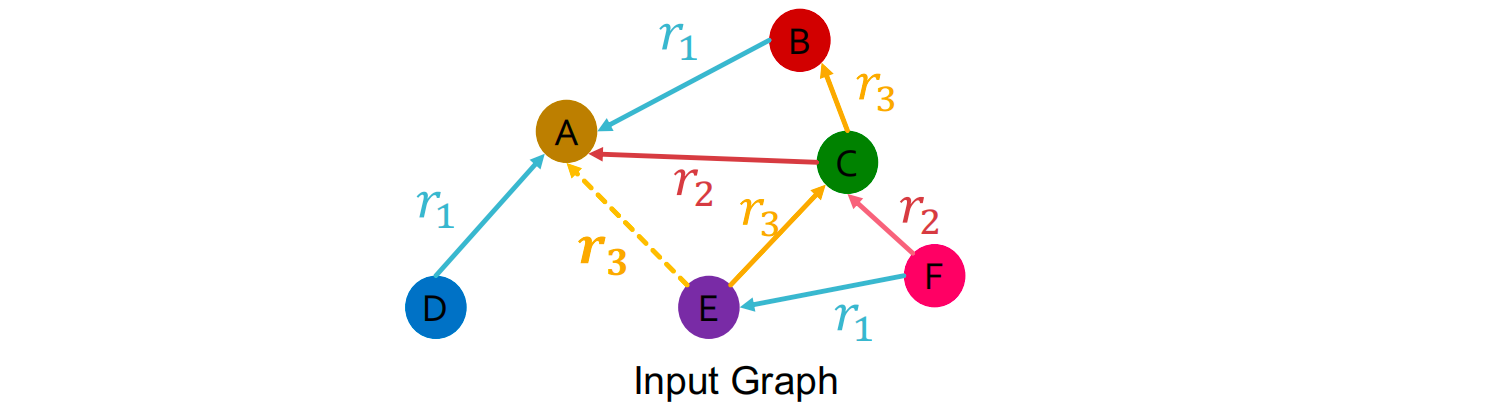
假设 $\left(E,r_3,A\right)$ 是training supervision edge，所有其他边都是training message edges。使用RGCN对 $\left(E,r_3,A\right)$ 进行评分：

• 取 $E$ 和 $A$ 的最后一层：$h_E^{(L)}$ 和 $h_A^{(L)}\in {\mathbb{R}}^d$。
• 关系特定的评分函数 $f_r$：${\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R}$
  • 例子：$f_{r_1}\left(h_E,h_A\right)=h_E^T{W}_{r_1}{h}_A,W_{r_1}\in {\mathbb{R}}^{d\times d}$

训练阶段：用 training message edges 预测 training supervision edges

1. 用RGCN给training supervision edge $(E,r_3,A)$ 打分
2. 通过perturb supervision edge 得到negative edge ：例如perturb $(E,r_3,A)$ 得到 $(E,r_3,B)$
3. 使用GNN计算 negative edge的分数
4. 优化交叉熵损失函数，使 training supervision edge 上得分最高，negative edge 上得分最低：
   1. $\ell =-\log \sigma \left(f_{r_3}(h_E,h_A)\right)-\log (1-\sigma (f_{r_3}(h_E,h_B)))$，$\sigma :Sigmoid$

验证阶段：用 training message edges 和 training supervision edges 预测 validation edges： $(E,r_3,D)$ 。 $(E,r_3,D)$ 的得分应该比所有不在 training message edges 和 training supervision edges 的点得分更高，比如 $(E,r_3,B)$

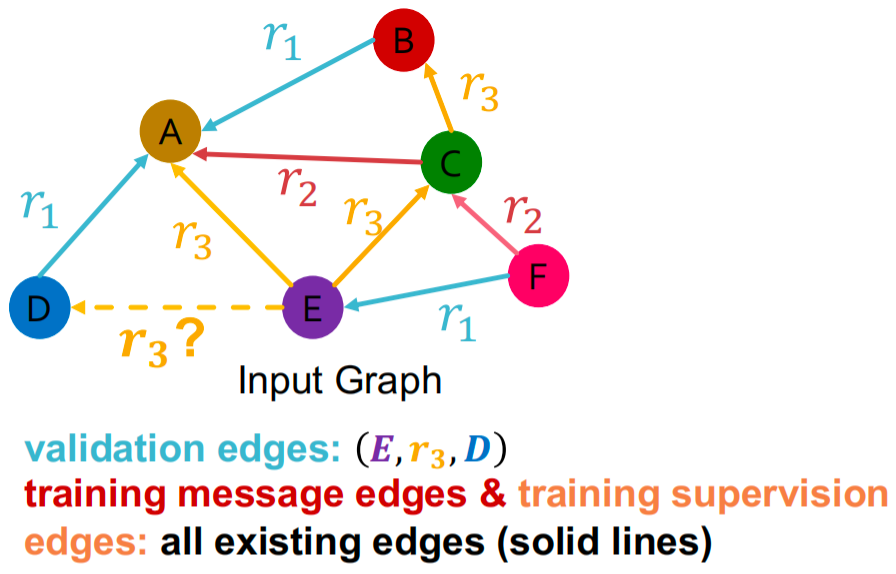
具体步骤：

1. 计算 $(E,r_3,D)$ 的得分
2. 计算所有 negetive edges 的得分 { ( E , r 3 , v ) ∣ v ∈ { B , F } } \{(E,r_3,v)|v\in\{B,F\}\} {(E,r3​,v)∣v∈{B,F}}
3. 获得 $(E,r_3,D)$ 的排名
4. 计算指标