OpenGL/GLUT实践:弹簧-质量-阻尼系统模拟摆动的绳子和布料的物理行为(电子科技大学信软图形与动画Ⅱ实验)
源码见GitHub:A-UESTCer-s-Code
文章目录
- 1 实现效果
- 2 实现过程
- 2.1 一维弹性物体模拟
- 2.1.1 质点类(Mass)
- 2.1.2 弹簧类(Spring)
- 2.1.3 模拟类(RopeSimulation)
- 2.1.4 openGL实现
- 2.2 二维弹性物体模拟
- 2.2.1 模拟类改进
- (1) Simulation1 类
- (2) ClothSimulation 类
- 2.2.2 openGL 渲染
- 2.2.3 鼠标互动
- 2.2.4 最终实现
1 实现效果
二维的弹性物体最终实现的效果如下:
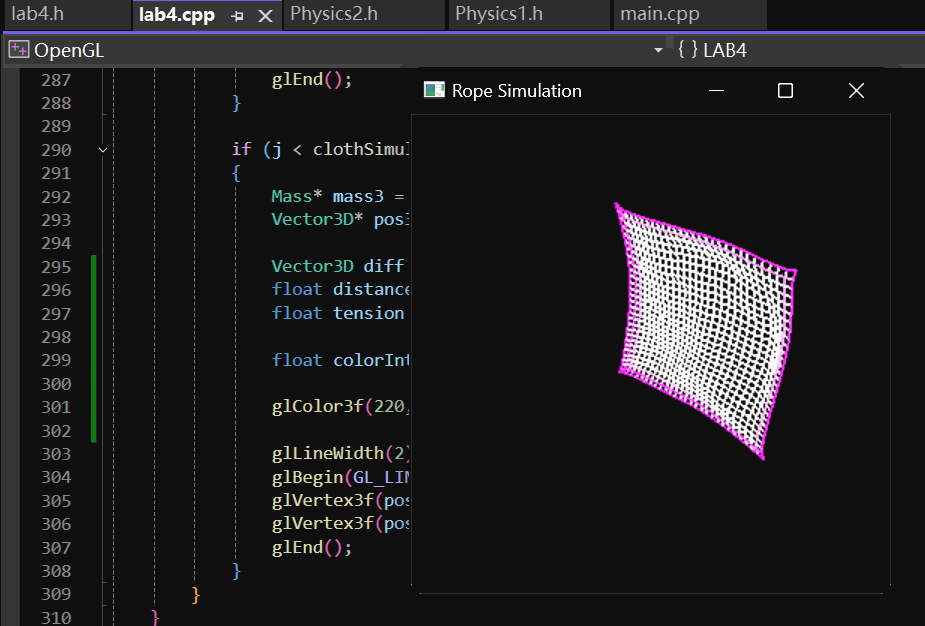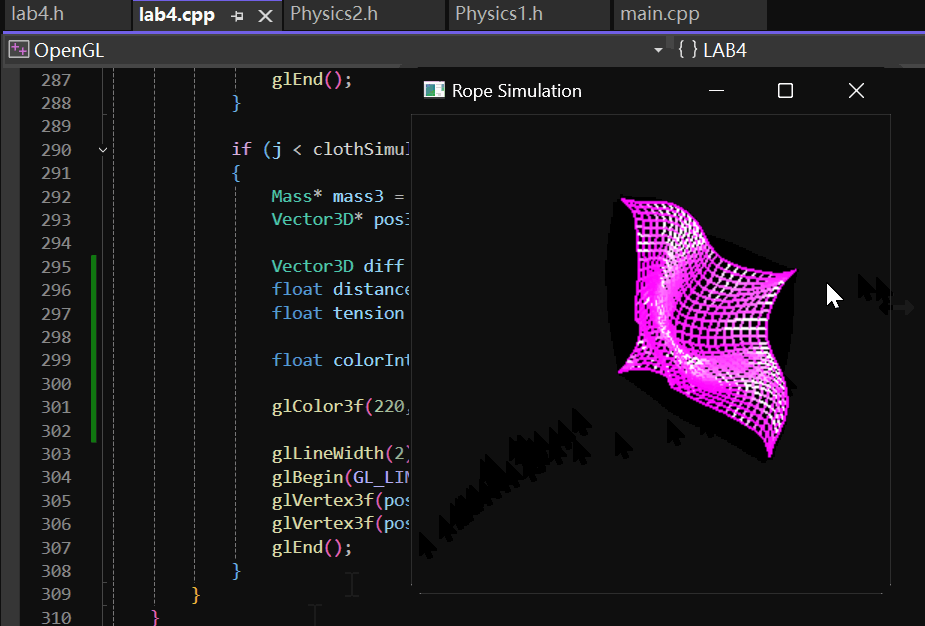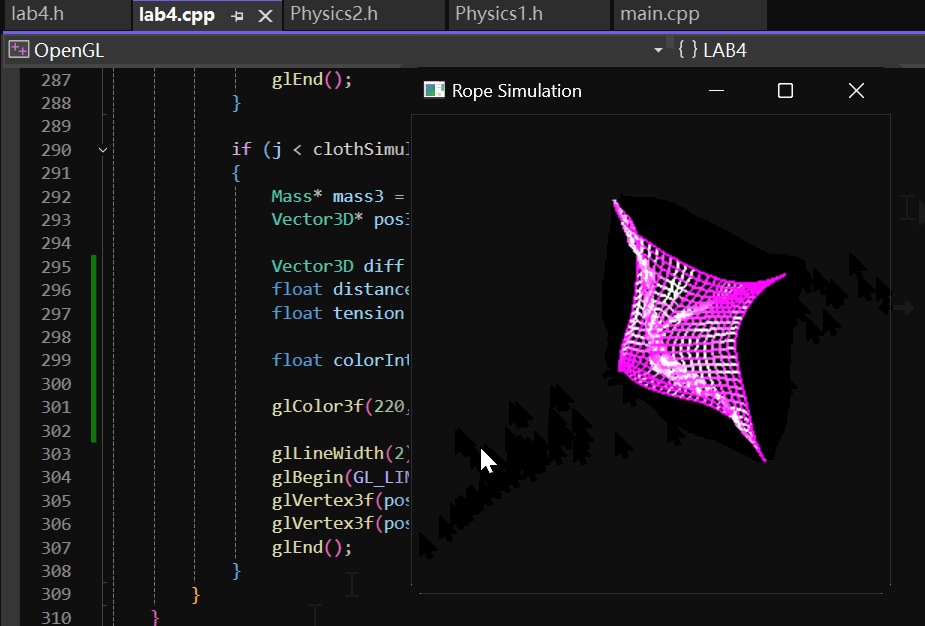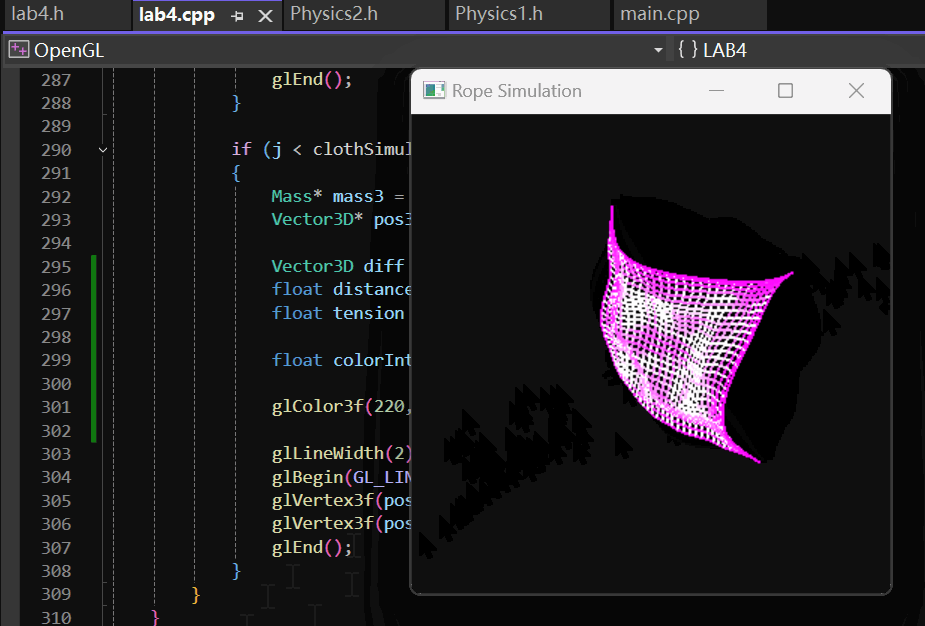
2 实现过程
2.1 一维弹性物体模拟
2.1.1 质点类(Mass)
质点类(Mass)是用于表示弹性物体中的单个质点的关键组件之一。在这个类中,我们记录了质点的基本信息,包括质量、位置、速度和受力。下面是对质点类中关键成员和方法的说明:
float m: 质点的质量。质量决定了质点对外力的响应程度。Vector3D pos: 质点在空间中的位置。位置向量用来描述质点的位置。Vector3D vel: 质点的速度。速度向量表示质点在各个方向上的运动速度。Vector3D force: 质点所受的外力。在每个时间步长内,质点可能受到多个外力的作用,这些外力的向量和即为质点所受的总外力。
以下是质点类中的关键方法:
applyForce(Vector3D force):用于将外力应用于质点上。在一段时间内,可能会有多个外部力作用于质点上,因此我们将这些外力向量相加,得到质点所受的总外力。init():初始化方法,将质点的外力值设为零。在每个时间步长开始时,我们需要将质点的外力重置为零,以便计算新的外力。simulate(float dt):模拟方法,根据质点所受的外力和牛顿运动定律,计算质点在时间步长dt内的新位置和新速度。这里采用了欧拉方法(Euler Method)进行数值积分,它虽然简单但通常足够用于大多数物理模拟。
质点类是模拟弹性物体运动过程中的基础,通过不断更新质点的状态,我们可以模拟出弹性物体在外力作用下的运动行为。
2.1.2 弹簧类(Spring)
弹簧类(Spring)是用于模拟弹簧连接的两个质点之间的作用力的关键组件。在这个类中,我们记录了弹簧的基本信息,包括连接的两个质点、弹簧的刚度和长度,以及内部阻尼的影响。下面是对弹簧类中关键成员和方法的说明:
Mass* mass1,Mass* mass2: 弹簧连接的两个质点。这两个质点受到弹簧作用的力,质点运动受到弹簧力的影响。float springConstant: 弹簧的刚度常数。它决定了弹簧对质点施加的力的大小。float springLength: 弹簧的静止长度。当两个质点的距离等于静止长度时,弹簧不会施加力。float frictionConstant: 弹簧的内部阻尼系数。它描述了弹簧内部摩擦的程度。
以下是弹簧类中的关键方法:
solve(): 解决方法,用于计算弹簧连接的两个质点受到的合力。
-
首先计算两个质点之间的距离,并根据距离计算弹簧的伸长量。
float r = springVector.length(); -
然后根据伸长量和弹簧的刚度常数计算弹簧对质点施加的力。
e = springVector / r;:计算弹簧的单位方向向量。springVector是弹簧两端质点之间的位移向量,通过除以该向量的长度r,可以得到单位方向向量e。force += e * (r - springLength) * (-springConstant);:计算弹簧的弹性力。根据胡克定律,弹簧的弹性力与弹簧的伸长量成正比,方向与弹簧的单位方向向量相同。r - springLength表示当前弹簧的伸长量,乘以弹簧的弹性常数springConstant,即可得到弹簧的弹性力大小。force += -e * (mass1->vel*e - mass2->vel*e) * frictionConstant;:计算弹簧的摩擦力。摩擦力与两个质点之间的相对速度以及弹簧的内摩擦常数成正比。(mass1->vel*e - mass2->vel*e)计算了两个质点之间的相对速度在弹簧方向上的分量,然后乘以内摩擦常数frictionConstant,即可得到摩擦力的大小。
-
最后,将弹簧力施加到两个质点上,以更新它们的受力状态。
弹簧类是模拟弹性物体运动过程中的关键组件之一,通过模拟弹簧连接的两个质点之间的作用力,我们可以模拟出弹簧在外力作用下的伸缩变形情况,从而实现对弹性物体的模拟。
2.1.3 模拟类(RopeSimulation)
模拟类是整个模拟系统的核心,负责协调质点和弹簧之间的相互作用,并模拟一维弹性物体的运动过程。在模拟类中,我们创建了弹簧数组,并初始化了所有的弹簧。然后,在每个时间步长内,我们通过迭代计算所有弹簧的受力情况,并更新所有质点的位置和速度。下面是对弹簧类中关键成员和方法的说明:
-
Spring** springs;:弹簧数组,用于存储所有弹簧对象的指针。 -
Vector3D gravitation;:表示重力加速度的向量,将作用于所有质点。 -
Vector3D ropeConnectionPos;:绳索连接点的位置向量,用于指定系统中第一个质点的位置。 -
Vector3D ropeConnectionVel;:绳索连接点的速度向量,用于移动绳索连接点。
以下是弹簧类中的关键方法:
-
RopeSimulation(...)构造函数:初始化模拟对象。在此构造函数中,我们设置了质点的初始位置,创建了弹簧对象,并将其连接到相应的质点上。 -
release()方法:释放内存,用于删除所有的弹簧对象。 -
solve()方法:计算系统中所有弹簧的受力情况,包括弹簧的弹性力和重力。然后将这些力应用于相应的质点上。 -
simulate(float dt)方法:模拟系统的运动过程。在每个时间步长内,首先调用基类的simulate()方法更新所有质点的位置和速度。然后更新绳索连接点的位置。 -
setRopeConnectionVel(Vector3D ropeConnectionVel)方法:设置绳索连接点的速度,用于移动绳索连接点。
通过这些方法,模拟类 RopeSimulation 能够模拟一维弹性物体的运动过程,并在其中考虑了重力、弹簧力以及绳索连接点的运动。
2.1.4 openGL实现
实现了一个基于OpenGL的绳索模拟系统,其中使用了一些物理引擎的概念,如质点、弹簧和重力。
RopeSimulation* ropeSimulation = new RopeSimulation(...);:创建了一个绳索模拟对象,设置了模拟所需的参数,如质点数量、质点重量、弹簧常数、弹簧长度等。void renderScene(void):渲染函数,绘制绳索模拟系统的图像,包括绳索的线条表示。- 首先,它设置了视图矩阵和模型矩阵,然后清除颜色缓冲区和深度缓冲区。
- 接着,调用了
Update()函数更新模拟系统的状态。 - 最后,通过OpenGL的绘图函数
glBegin()和glEnd()绘制了绳索的形状,以线段的形式连接相邻的质点。绘制完成后,刷新绘图管线并交换缓冲区,使绘制结果显示在屏幕上。
这段代码通过OpenGL实现了一个基本的绳索模拟系统,并提供了键盘控制功能,用户可以通过键盘输入控制绳索的运动方向和停止模拟等。
实现效果如下:

2.2 二维弹性物体模拟
接下来我们要实现一个二维的弹性物体——布料,其就是将之前实现的弹性绳子交叉纵横编织成一个网。
2.2.1 模拟类改进
(1) Simulation1 类
Simulation1 类在 Simulation 类的基础上进行了扩展,以支持二维的弹性物体模拟,而不仅仅是一维的质点链。以下是主要的改进:
-
二维质点数组:在
Simulation类中,质点存储在一个一维数组中。在Simulation1类中,质点存储在一个二维数组中,这使得可以模拟一个二维的弹性物体,如布料。Mass*** masses; // In Simulation1 Mass** masses; // In Simulation -
构造函数:
Simulation1的构造函数接受两个参数,分别表示二维物体的行数和列数,而Simulation的构造函数只接受一个参数,表示一维质点链的长度。Simulation1(int numOfMassX, int numOfMassY, float m) // In Simulation1 Simulation(int numOfMasses, float m) // In Simulation -
获取质点的方法:
Simulation1类提供了一个新的getMass(int x, int y)方法,可以获取二维数组中的任何一个质点。而Simulation类只提供了一个getMass(int index)方法,只能获取一维数组中的质点。Mass* getMass(int x, int y) // In Simulation1 Mass* getMass(int index) // In Simulation -
初始化和模拟方法:
Simulation1类的init()和simulate(float dt)方法都使用了两层循环,以处理二维数组中的所有质点。而Simulation类的这两个方法只使用了一层循环,只处理一维数组中的质点。for (int i = 0; i < row; ++i) for (int j = 0; j < col; ++j) masses[i][j]->init(); // In Simulation1 for (int a = 0; a < numOfMasses; ++a) masses[a]->init(); // In Simulation
Simulation1 类在 Simulation 类的基础上进行了扩展,以支持二维的弹性物体模拟。
(2) ClothSimulation 类
ClothSimulation类在RopeSimulation类的基础上进行了一些改动以模拟布料的物理行为。以下是一些主要的改动:
ClothSimulation类引入了Xlen和Ylen两个变量,它们分别表示布料在X轴和Y轴方向上的质点数量。这与RopeSimulation类不同,后者只需要一个质点数组来模拟一维的绳索。ClothSimulation类的构造函数接受两个额外的参数numOfMassesX和numOfMassesY,它们分别表示布料在X轴和Y轴方向上的质点数量。这与RopeSimulation类的构造函数不同,后者只需要一个参数来表示质点的数量。ClothSimulation类的springs变量是一个四维数组,用于存储布料中的弹簧。每个弹簧都连接着两个相邻的质点。这与RopeSimulation类不同,后者的springs变量是一个二维数组,只需要存储绳索中的弹簧。ClothSimulation类的simulate方法更新了四个角的质点位置(固定了四个角)和速度,以模拟布料的运动。这与RopeSimulation类的simulate方法不同,后者只更新了第一个质点的位置和速度。
2.2.2 openGL 渲染
renderScene() 主要思想是遍历布料模拟中的所有质点,并绘制连接这些质点的弹簧。弹簧的颜色和宽度由其张力决定。
-
通过两层循环遍历所有质点。每个质点都与其右侧和下方的质点相连,形成一个弹簧。
if (i < clothSimulation->Xlen - 2)和if (j < clothSimulation->Ylen - 2)这两个条件判断确保了不会尝试访问超出数组范围的质点。 -
对于每个弹簧,计算其两端质点的距离,以此计算张力。
-
根据张力计算颜色强度,张力越大,颜色强度越小。
-
使用OpenGL的函数设置线段的颜色和宽度,然后绘制线段。
这样,就可以在屏幕上绘制出一个由弹簧组成的网格,模拟布料的效果。
2.2.3 鼠标互动
mouse() 和 motion() 主要处理鼠标的点击和移动事件,以便在布料模拟中选择和移动质点。
mouse函数处理鼠标点击事件。当左键被按下时,它会记录鼠标的状态和位置,并将鼠标的屏幕坐标转换为模拟空间的坐标。然后,它会遍历所有的质点,找到距离鼠标位置最近的质点,并记录其位置。当左键被释放时,它会重置鼠标的状态。motion函数处理鼠标移动事件。当左键被按下时,它会将鼠标的屏幕坐标转换为模拟空间的坐标,并计算出鼠标移动的距离。然后,它会更新被选中质点的位置,使其沿着鼠标移动的方向移动。最后,它会更新鼠标的位置。
这样就可以通过鼠标操作来选择和移动布料模拟中的质点,从而直观地观察和控制布料的运动。
2.2.4 最终实现
最终实现的效果如下:

