当前位置：首页 > article >正文

代码随想录训练营 Day51打卡图论part02 99. 岛屿数量 100. 岛屿的最大面积

article 2024/11/16 19:42:07

代码随想录训练营 Day51打卡图论part02

一、卡码99. 岛屿数量

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。
后续 N 行，每行包含 M 个数字，数字为 1 或者 0。
输出描述
输出一个整数，表示岛屿的数量。如果不存在岛屿，则输出 0。
输入示例
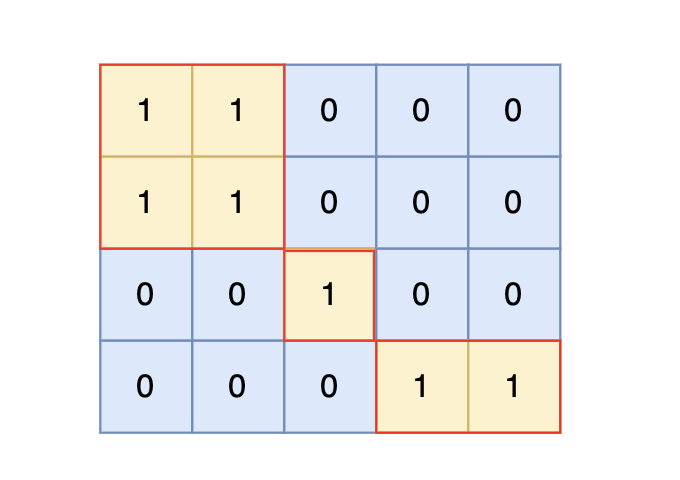
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
3
提示信息

根据测试案例中所展示，岛屿数量共有 3 个，所以输出 3。

核心步骤：
深度优先搜索 (DFS)：当找到一块未访问的陆地时，使用 DFS 遍历所有与它相邻的陆地，并标记为已访问。DFS 会递归地访问所有四个方向上的相邻陆地。
计数岛屿：每找到一个新的未访问的陆地，岛屿数加一，同时使用 DFS 标记所有相邻的陆地，防止重复计数。
边界检查：每次访问新的坐标时，需要确保坐标合法（不越界）且是未访问的陆地。

DFS

# 定义四个方向：上、右、下、左
direction = [[0, 1], [1, 0], [0, -1], [-1, 0]]  # 上右下左四个方向

def dfs(grid, visited, x, y):
    """
    对一块陆地进行深度优先遍历并标记
    :param grid: 二维网格，1 代表陆地，0 代表水
    :param visited: 记录哪些节点被访问过
    :param x: 当前节点的行索引
    :param y: 当前节点的列索引
    """
    for i, j in direction:
        next_x = x + i
        next_y = y + j
        # 判断坐标是否越界
        if next_x < 0 or next_x >= len(grid) or next_y < 0 or next_y >= len(grid[0]):
            continue  # 越界直接跳过
        # 如果是未访问的陆地，进行递归遍历
        if not visited[next_x][next_y] and grid[next_x][next_y] == 1:
            visited[next_x][next_y] = True  # 标记为已访问
            dfs(grid, visited, next_x, next_y)  # 递归调用，继续深度遍历

if __name__ == '__main__':
    # 输入网格的大小：n 表示行数，m 表示列数
    n, m = map(int, input().split())
    
    # 构建网格 (邻接矩阵表示法)
    grid = []
    for i in range(n):
        grid.append(list(map(int, input().split())))  # 每行输入网格

    # 初始化访问表，标记哪些节点已访问过
    visited = [[False] * m for _ in range(n)]
    
    # 岛屿计数结果
    res = 0
    # 遍历网格的每个点
    for i in range(n):
        for j in range(m):
            # 如果当前点是未访问的陆地
            if grid[i][j] == 1 and not visited[i][j]:
                res += 1  # 找到一个新的岛屿，岛屿数加 1
                visited[i][j] = True  # 标记为已访问
                dfs(grid, visited, i, j)  # 对该点进行深度优先搜索，标记相邻的陆地

    # 输出岛屿的数量
    print(res)

BFS 实现思路：

队列
(Queue)：使用队列来保存当前层需要访问的节点，每次从队列中取出一个节点，将其所有相邻的未访问陆地加入队列，直到所有与该节点相连的陆地都遍历完。
邻接矩阵表示：同样使用二维数组（邻接矩阵）表示网格，1 表示陆地，0 表示水。
计数岛屿：每次找到一个新的未访问陆地时，岛屿数量加 1，使用 BFS 来遍历整个岛屿，确保该岛屿上的所有陆地都被标记为已访问。

BFS

from collections import deque

# 定义四个方向：上、右、下、左
direction = [[0, 1], [1, 0], [0, -1], [-1, 0]]  # 上、右、下、左

def bfs(grid, visited, x, y):
    """
    使用 BFS 遍历和标记岛屿
    :param grid: 二维网格，1 代表陆地，0 代表水
    :param visited: 记录哪些节点被访问过
    :param x: 起点的行索引
    :param y: 起点的列索引
    """
    # 初始化一个队列，将起点加入队列并标记为已访问
    queue = deque()
    queue.append((x, y))
    visited[x][y] = True  # 标记起点已访问

    # 开始广度优先搜索
    while queue:
        cur_x, cur_y = queue.popleft()  # 从队列中取出当前节点
        
        # 遍历当前节点的四个相邻方向
        for i, j in direction:
            next_x = cur_x + i
            next_y = cur_y + j
            # 判断是否越界以及是否是未访问的陆地
            if 0 <= next_x < len(grid) and 0 <= next_y < len(grid[0]):
                if not visited[next_x][next_y] and grid[next_x][next_y] == 1:
                    # 如果是未访问的陆地，加入队列并标记为已访问
                    visited[next_x][next_y] = True
                    queue.append((next_x, next_y))

if __name__ == '__main__':
    # 输入网格的大小：n 表示行数，m 表示列数
    n, m = map(int, input().split())
    
    # 构建网格 (邻接矩阵表示法)
    grid = [list(map(int, input().split())) for _ in range(n)]

    # 初始化访问表，标记哪些节点已访问过
    visited = [[False] * m for _ in range(n)]
    
    # 岛屿计数结果
    res = 0
    # 遍历网格的每个点
    for i in range(n):
        for j in range(m):
            # 判断：如果当前节点是未访问的陆地
            if grid[i][j] == 1 and not visited[i][j]:
                res += 1  # 找到一个新的岛屿，岛屿数加 1
                bfs(grid, visited, i, j)  # 使用 BFS 搜索并标记该岛屿

    # 输出岛屿的数量
    print(res)

总结

BFS 通过使用队列逐层访问相邻节点，非常适合处理需要按层次逐步扩展的搜索问题。
DFS 适合更深层次的递归搜索，而 BFS 更注重广度、层次上的扩展。对于岛屿计数问题，BFS 和 DFS都可以高效解决，关键在于如何标记已访问的节点，防止重复计数。

题目链接
题目文章讲解

二、卡码100. 岛屿的最大面积

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。后续 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。
输出描述
输出一个整数，表示岛屿的最大面积。如果不存在岛屿，则输出 0。
输入示例
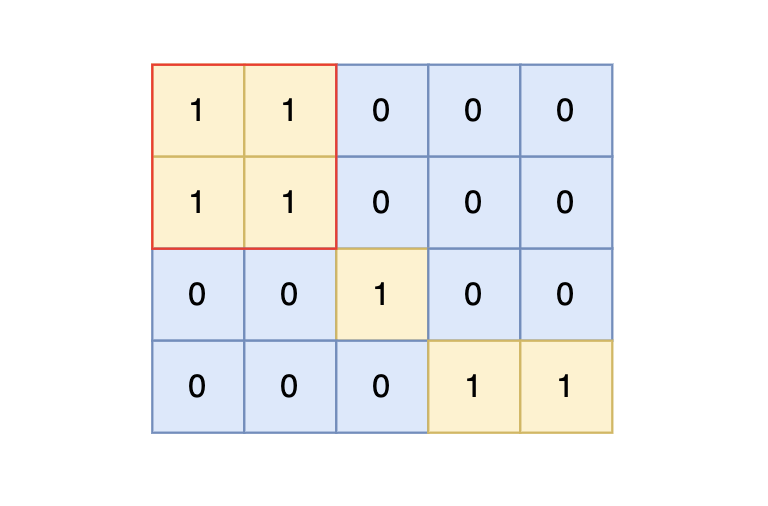
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
4
提示信息

样例输入中，岛屿的最大面积为 4。

主要步骤：

深度优先搜索 (DFS)：对于每块未访问的陆地（grid[i][j] == 1 且 visited[i][j] == False），使用DFS 遍历所有与它相连的陆地块，并统计连通区域的大小。DFS 递归遍历四个方向，确保所有相连的陆地都被访问。
计数连通陆地的面积：每次通过 DFS 遍历完一块连通的陆地块后，记录该区域的大小，并在所有遍历完成后输出最大的区域面积。
全局变量 count：在 DFS 中使用全局变量 count 来记录当前遍历到的连通陆地块的大小。每次发现一块新陆地时，count 从1 开始计数，DFS 过程中每找到一块相邻的陆地块，count 增加 1。

代码实现

# 定义四个方向：上、右、下、左
position = [[0, 1], [1, 0], [0, -1], [-1, 0]]
count = 0  # 全局变量，用于记录当前连通陆地的面积

def dfs(grid, visited, x, y):
    """
    深度优先搜索，遍历并标记一整块连通的陆地
    :param grid: 二维网格，1 代表陆地，0 代表水
    :param visited: 记录哪些节点被访问过
    :param x: 当前节点的行索引
    :param y: 当前节点的列索引
    """
    global count  # 使用全局变量 count 记录当前连通区域的面积
    for i, j in position:  # 遍历四个方向：上、右、下、左
        cur_x = x + i
        cur_y = y + j
        # 判断坐标是否越界
        if cur_x < 0 or cur_x >= len(grid) or cur_y < 0 or cur_y >= len(grid[0]):
            continue  # 如果越界，跳过该方向
        # 如果当前节点是未访问的陆地块，继续递归遍历
        if not visited[cur_x][cur_y] and grid[cur_x][cur_y] == 1:
            visited[cur_x][cur_y] = True  # 标记为已访问
            count += 1  # 当前连通陆地面积加 1
            dfs(grid, visited, cur_x, cur_y)  # 递归搜索相邻的陆地块

# 主函数，读取输入并处理
n, m = map(int, input().split())  # 输入网格的大小 n 行 m 列
# 构建网格，读取每行输入作为网格的一部分
grid = []
for i in range(n):
    grid.append(list(map(int, input().split())))  # 每行输入陆地/水域信息
# 初始化访问数组，记录哪些节点已访问过
visited = [[False] * m for _ in range(n)]

result = 0  # 记录所有连通陆地块中的最大面积
# 遍历整个网格
for i in range(n):
    for j in range(m):
        # 如果当前节点是未访问的陆地块，开始新的 DFS 遍历
        if grid[i][j] == 1 and not visited[i][j]:
            count = 1  # 初始化当前连通区域的面积为 1
            visited[i][j] = True  # 标记当前节点为已访问
            dfs(grid, visited, i, j)  # 使用 DFS 遍历相连的陆地块
            result = max(count, result)  # 更新最大的连通区域面积

# 输出结果，最大连通陆地面积
print(result)