当前位置： 首页 > article >正文

算法复盘——Leetcode hot100: 双指针算法

article 2024/11/14 0:35:39

双指针算法

11. 盛最多水的容器 - 力扣（LeetCode）

优化解法：用 left 和 right 两个指针从两端向中心收缩，一边收缩一边计算 [left, right] 之间的矩形面积，取最大的面积值即是答案。
在这里插入图片描述

其实是优化区间选择 直接丢弃体积一定会减小的区间 （通过指针移动 直到两个指针重合

遍历数组一遍O(n)

class Solution { 
public int maxArea(int[] height) { 
int left = 0, right = height.length - 1; 
int res = 0; while (left < right) { // [left, right] 之间的矩形面积 
int cur_area = Math.min(height[left], height[right]) * (right - left); 
res = Math.max(res, cur_area); // 双指针技巧，移动较低的一边 
if (height[left] < height[right]) { 
left++; } 
else { right--; 
} 
} return res;
 } 
 }

15. 三数之和 - 力扣（LeetCode）

  • 关键： 三个数的下标互不相等，和为0 返回三元数组
  • 答案中不可以包含重复的三元组
  • 难点：三元组去重

暴力解法：排序+暴力枚举+利用SET去重，会超时

  • 错误代码
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);//排序
        HashSet<List<Integer>> hash = new HashSet<>();
        int[] record = new int[3];
        List<List<Integer>> ret = new ArrayList<>();
        for(int i = 0;i < nums.length;i++){
            for(int j = 0;j < nums.length;j++){
                for(int k = 0;k < nums.length;k++){
                    while(i != j && i != k && j!=k){
                    if(nums[i] + nums[j] + nums[k] == 0){
                        record.add(hash.add(nums[i],nums[j],nums[k]))
                    }
                    }
                }
            }
        }
    return ret.add(record);
    }
}

错误分析

  1. 使用 HashSet 存储 List：
    HashSet 不适合直接存储 List，因为它需要元素具有 hashCode() 和 equals() 方法的正确实现来确保唯一性。而 List 的 hashCode() 和 equals() 方法默认是基于对象内存地址的，这意呀着即使两个 List 包含相同的元素，它们也被视为不同的对象。
  2. 使用 while 循环进行条件判断：
    在三层嵌套循环中使用 while 循环进行条件判断是不必要的，且逻辑上也不正确。您应该直接在 if 语句中检查条件。
  3. 添加元素到 List 和 HashSet 的方式错误：
    record.add(hash.add(nums[i],nums[j],nums[k])) 这行代码是错误的，因为 HashSet 没有 add(int, int, int) 方法，且 record 是一个 int 数组，不能添加 List 或其他对象。
  4. 返回结果的处理：
    return ret.add(record); 这行代码也是错误的，因为 add() 方法返回的是布尔值（表示是否成功添加），而不是 List。您应该直接返回 ret。
  5. 去重和排序问题：
    由于您已经对数组进行了排序，可以利用这一点来避免重复和减少不必要的计算。

数组有序考虑二分查找 双指针

  • 双指针能让复杂度低一个指数

优化思路：指针到一个数t,剩下有序数组存两个数，和为t的相反数 两数之和

重难点：去重 两个地方，不走重复的数 ，避免越界
在这里插入图片描述

去重逻辑的思考

a的去重

说到去重，其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i]，nums[left]，nums[right]

a 如果重复了怎么办，a是nums里遍历的元素，那么应该直接跳过去。

但这里有一个问题，是判断 nums[i] 与 nums[i + 1]是否相同，还是判断 nums[i] 与 nums[i-1] 是否相同。

其实不一样！

都是和 nums[i]进行比较，是比较它的前一个，还是比较它的后一个。

如果我们的写法是 这样：

if (nums[i] == nums[i + 1]) { // 去重操作
    continue;
}

那我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据，当遍历到第一个-1 的时候，判断 下一个也是-1，那这组数据就pass了。

我们要做的是 不能有重复的三元组，但三元组内的元素是可以重复的！

所以这里是有两个重复的维度。

那么应该这么写：

if (i > 0 && nums[i] == nums[i - 1]) {
    continue;
}

这么写就是当前使用 nums[i]，我们判断前一位是不是一样的元素，在看 {-1, -1 ,2} 这组数据，当遍历到 第一个 -1 的时候，只要前一位没有-1，那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。

这是一个非常细节的思考过程。

b与c的去重
while (right > left) {
    if (nums[i] + nums[left] + nums[right] > 0) {
        right--;
        // 去重 right
        while (left < right && nums[right] == nums[right + 1]) right--;
    } else if (nums[i] + nums[left] + nums[right] < 0) {
        left++;
        // 去重 left
        while (left < right && nums[left] == nums[left - 1]) left++;
    } else {
    }
}

但细想一下，这种去重其实对提升程序运行效率是没有帮助的。

拿right去重为例，即使不加这个去重逻辑，依然根据 while (right > left) 和 if (nums[i] + nums[left] + nums[right] > 0) 去完成right-- 的操作。

多加了 while (left < right && nums[right] == nums[right + 1]) right--; 这一行代码，其实就是把 需要执行的逻辑提前执行了，但并没有减少 判断的逻辑。

最直白的思考过程，就是right还是一个数一个数的减下去的，所以在哪里减的都是一样的。

所以这种去重 是可以不加的。 仅仅是 把去重的逻辑提前了而已。

  • 正确答案
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
	// 找出a + b + c = 0
        // a = nums[i], b = nums[left], c = nums[right]
        for (int i = 0; i < nums.length; i++) {
	    // 排序之后如果第一个元素已经大于零，那么无论如何组合都不可能凑成三元组，直接返回结果就可以了
            if (nums[i] > 0) { 
                return result;
            }

            if (i > 0 && nums[i] == nums[i - 1]) {  // 去重a
                continue;
            }

            int left = i + 1;
            int right = nums.length - 1;
            while (right > left) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
		    // 去重逻辑应该放在找到一个三元组之后，对b 和 c去重
                    while (right > left && nums[right] == nums[right - 1]) right--;
                    while (right > left && nums[left] == nums[left + 1]) left++;
                    
                    right--; 
                    left++;
                }
            }
        }
        return result;
    }
}

42. 接雨水 - 力扣（LeetCode）

头脑风暴ing: 存在 >= 自己的数 怎么求和？

突破点：仅仅对于位置 i，能装下多少水呢？

img

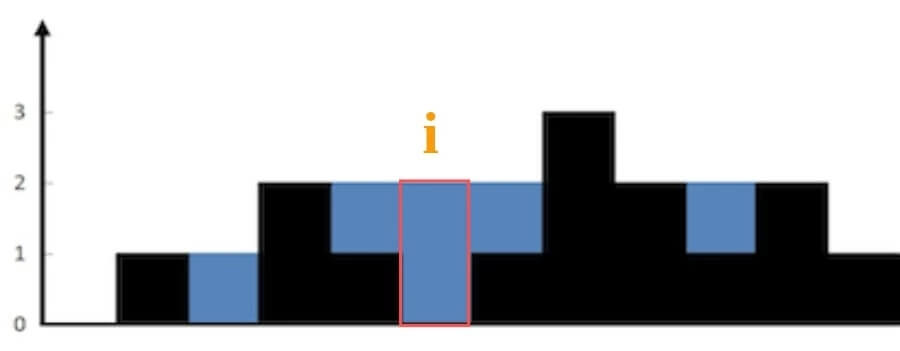
能装 2 格水，因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。

为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 l_max 和 r_max；位置 i 最大的水柱高度就是 min(l_max, r_max)。

  • 错误暴力 会超时
  • 在每个位置 i 都要计算每次都遍历
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) return 0;
        int sum = 0;
        //int mleft = 0;//错误
        //int mright = 0;//错误 应该为当前高度
        for(int i = 1; i < n; i++){
            int mleft = height[i];
            int mright = height[i];
            //maxleft
            for(int j = i - 1;j >= 0 ;){
                mleft = Math.max(mleft,height[j]);
                j--;
                }
            //maxright
            for (int z = i + 1; z < n ;){
                mright = Math.max(mright,height[z]);
                z++;
            }
            sum = Math.min(mleft,mright);
            sum = sum + sum;
            }
            return sum;
        }
        
    }
  • 优化 备忘录 提前算出

我们开两个数组 r_max 和 l_max 充当备忘录，l_max[i] 表示位置 i 左边最高的柱子高度，r_max[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组计算好，避免重复计算：

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) return 0;
        int sum = 0;
        int[] mleft = new int[n];
        int[] mright = new int[n];
        mleft[0] = height[0];
        mright[n-1] = height[n -1];
        //maxleft
        for(int i = 1 ;i < n ;i++){
                mleft[i] = Math.max(height[i],height[i-1]);
                }//错误 动态规划思路 
        //maxright
        for (int i = n - 2; i >= 0; i--){
                mright[i] = Math.max(height[i],height[i+1]);
            }//错误代码 动态规划思路
        for(int i = 1; i < n-1; i++){
             sum += Math.min(mleft[i],mright[i]) - height[i];
            }
            return sum;
        }
        
    }
  • 正确代码
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) return 0;
        int sum = 0;
        int[] mleft = new int[n];
        int[] mright = new int[n];
        mleft[0] = height[0];
        mright[n-1] = height[n -1];
        //maxleft
        for(int i = 1 ;i < n ;i++){
                mleft[i] = Math.max(height[i],mleft[i-1]);
                }
        //maxright
        for (int i = n - 2; i >= 0; i--){
                mright[i] = Math.max(height[i],mright[i+1]);
            }
        for(int i = 1; i < n-1; i++){
             sum += Math.min(mleft[i],mright[i]) - height[i];
            }
            return sum;
        }
        
    }

代码解析

初始化mleft数组

for (int i = 1; i < n; i++) {    
    mleft[i] = Math.max(mleft[i - 1], height[i]);    
}
  • mleft数组用于存储每个位置i及其左侧的最大柱子高度。
  • 初始化时，我们将mleft[0]设为height[0]（虽然代码中未显示，但根据上下文可以推断）。
  • 从索引1开始遍历至n-1，对于每个位置i，mleft[i]的值为mleft[i-1]（即前一个位置的最大高度）与height[i]（当前位置的高度）中的较大者。
  • 这样，遍历完成后，mleft数组将包含每个位置及其左侧的最大柱子高度。

初始化并计算mright数组

// Initialize the last element of mright as it is    
mright[n - 1] = height[n - 1];  
  
// Calculate max height from right to left    
for (int i = n - 2; i >= 0; i--) {    
    mright[i] = Math.max(mright[i + 1], height[i]);    
}
  • mright数组用于存储每个位置i及其右侧的最大柱子高度。
  • 我们将mright[n-1]初始化为height[n-1]，即最右侧柱子的高度。
  • 从索引n-2开始逆向遍历至0，对于每个位置i，mright[i]的值为mright[i+1]（即后一个位置的最大高度）与height[i]（当前位置的高度）中的较大者。
  • 遍历完成后，mright数组将包含每个位置及其右侧的最大柱子高度。

计算雨水量

在得到mleft和mright数组后，我们可以计算每个位置所能接住的雨水量。雨水量由左右两侧最大高度的较小值减去当前位置的高度决定（但这部分代码在您提供的片段中未展示）。

通过动态规划的方法，首先计算出每个位置左侧和右侧的最大柱子高度，为后续计算雨水量奠定了基础。这种方法的时间复杂度为O(n)，空间复杂度也为O(n)，因为我们需要使用两个额外的数组来存储最大高度信息。


http://www.kler.cn/a/293979.html

相关文章：

  • springboot项目中，使用ProGuard 对代码进行混淆
  • Autosar CP DDS规范导读
  • RS®SZM 倍频器
  • ❤React-JSX语法认识和使用
  • 计算机的错误计算（一百五十二）
  • Linux下MySQL的简单使用
  • 软件测试基础总结+面试八股文
  • Vue2电商项目(二) Home模块的开发；（还需要补充js节流和防抖的回顾链接）
  • 数据结构（单向链表）
  • 软文发稿相比其他广告形式有哪些持续性优势？
  • 如何从硬盘恢复已删除/丢失的文件？硬盘恢复已删除的文件技巧
  • 如何录制黑神话悟空的游戏BGM导入iPhone手机制作铃声？
  • notepad下载安装使用以及高级使用技巧
  • Vue 中 nextTick 的最主要作用是什么，为什么要有这个 API
  • spring项目使用邮箱验证码校验
  • Vue3状态管理Pinia
  • APS开源源码解读: 排程工具 optaplanner
  • PHP批量修改MySQL数据表字符集为utf8mb4/utf8mb4_unicode_ci
  • 全网首发！！！opencv三通道Mat点云转halcon点云—HTuple类型
  • linux编译出现报错
  • ★ 算法OJ题 ★ 力扣3 - 无重复字符的最长子串
  • 百家云 BRTC：革新华为 HarmonyOS NEXT 系统的实时通信体验
  • ctfshow-php特性(web123-web150plus)
  • 安卓玩机工具-----ADB方式的刷机玩机工具“秋之盒”’ 测试各项功能预览
  • SpinalHDL之数据类型（一）
  • 【LeetCode】11.盛最多水的容器