【剑指offer】旋转数组的最小数字

- 👑专栏内容:剑指offer
- ⛪个人主页:子夜的星的主页
- 💕座右铭:前路未远,步履不停
目录
- 一、题目描述
- 1、题目
- 2、示例
- 示例1
- 示例2
- 二、题目分析
- 1、暴力法
- 2、二分法
- 三、代码汇总
- 1、暴力法
- 2、二分法
一、题目描述
1、题目
剑指offer:旋转数组的最小数字
有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。

2、示例
示例1
输入:[3,4,5,1,2]
输出:1
示例2
输入:[3,100,200,3]
输出:3
二、题目分析
1、暴力法
旋转数组的原数组是一个非降序数组,也就是说,原数组中的元素是按照从小到大的顺序排列的。当将一个非降序数组旋转后,我们可以把旋转数组分为两部分,一部分是最大的一段非降序子数组,另一部分是最小的一段非降序子数组。旋转数组的最小元素就在这两部分之间。比如,数组[3, 4, 5,1,2] 它的最大的一段非降序子数组是[3,4,5]最小的一段非降序子数组是[1,2] ,而最小元素就是最小的非降序子数组的第一个数。
所以说,非降序数组在旋转之后有一个特征,就是在遍历的时候,原始数组是非递减的,旋转之后,就有可能出现递减,而引起递减的数字,就是最小值。
class Solution {
public:
int minArray(vector<int>& numbers) {
int n = numbers.size(); //(1)
int min = numbers[0]; //(2)
for(int i = 1;i<n;i++) //(3)
{
if(numbers[i] < numbers[i-1]) //(4)
{
min = numbers[i];
break; //(5)
}
}
return min;
}
};
(1)获取旋转数组的长度
(2)让旋转数组中第一个元素为最小值
(3)从第二个元素开始遍历旋转数组
(4)如果当前元素比前一个元素小,证明引出现了递减,那么当前元素就是旋转数组的最小元素
(5)找到了最小元素,跳出循环
2、二分法
我们要知道一件事,暴力查找的过程,本质是排除的过程,但是暴力遍历一次只能排除一个,效率过低。既然是查找,我们就可以用二分查找法来缩减时间复杂度。
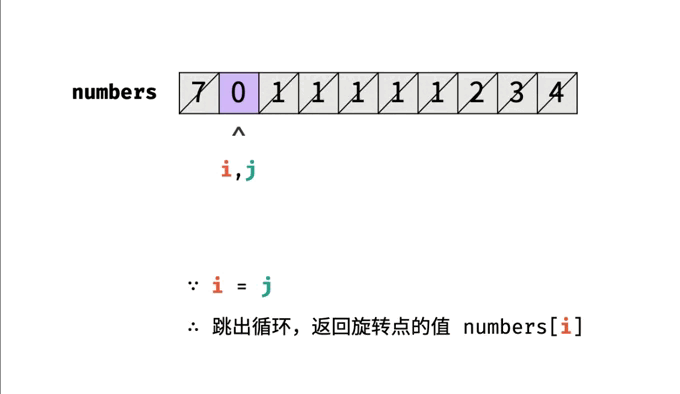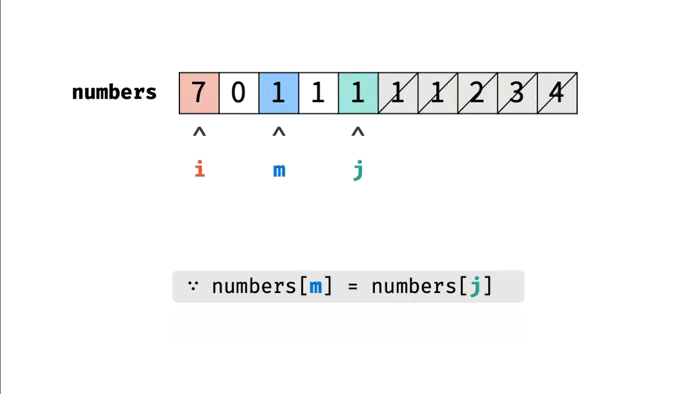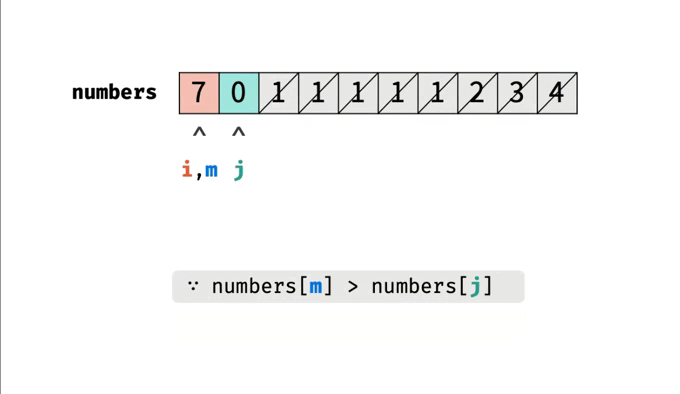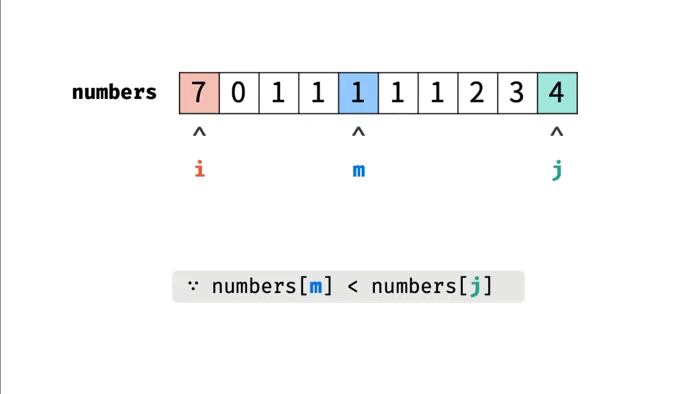
前面分析过,旋转数组的最小值位于非降序子数组和旋转子数组的交界处。所以,我们可以使用二分查找来查找旋转子数组的第一个元素,也就是最小值。旋转数组的最小值一定在数组的旋转点左侧或者就是旋转点。因此,在查找过程中,我们需要缩小查找区间,尽可能保留可能包含最小值的区间使用left和right指针确定查找区间,缩小区间的方式是根据mid的值与right的值的大小关系进行判断。如果numbers[mid]>numbers[right],说明最小值在mid的右侧,将left指针移动到mid+1的位置;如果numbers[mid]<numbers[right],说明最小值在mid的左侧或者就是mid,将right指针移动到mid的位置;如果numbers[mid] == numbers[right],说明可能是一个旋转点,也可能不是,将right指针移动一位。
class Solution {
public:
int minArray(vector<int>& numbers) {
int n = numbers.size();
int left = 0,right = n-1;
//二分查找
while(left<right)
{
int mid = (left + right)/2;
if(numbers[mid]>numbers[right])
left = mid + 1;
else if (numbers[mid]<numbers[right])
right = mid;
else
right --;
}
return numbers[left];
}
};
三、代码汇总
1、暴力法
class Solution {
public:
int minArray(vector<int>& numbers) {
int n = numbers.size();
int min = numbers[0];
for(int i = 1;i<n;i++)
{
if(numbers[i] < numbers[i-1])
{
min = numbers[i];
break;
}
}
return min;
}
};
2、二分法
class Solution {
public:
int minArray(vector<int>& numbers) {
int n = numbers.size();
int left = 0,right = n-1;
//二分查找
while(left<right)
{
int mid = (left + right)/2;
if(numbers[mid]>numbers[right])
left = mid + 1;
else if (numbers[mid]<numbers[right])
right = mid;
else
right --;
}
return numbers[left];
}
};
