5G网络建设
题目描述
现需要在基城市进行5G网络建设,已经选取N个地点设置5G基站,编号固定为1到N,接下来需要各个基站之间使用光纤进行连接以确保基
站能互联互通,不同基站之间假设光纤的成本各不相同,且有些节点之间已经存在光纤相连。
请你设计算法,计算出能联通这些基站的最小成本是多少。
注意:基站的联通具有传递性,比如基站A与基站B架设了光纤,基站B与基站C也架设了光纤,则基站A与基站C视为可以互相联通。
输入描述
第一行输入表示基站的个数N,其中:
- 0<N≤20
第二行输入表示具备光纤直连条件的基站对的数目M,其中:
- O<M<N*(N-1)/2
从第三行开始连续输入M行数据,格式为
- XYZP
其中:
X,Y表示基站的编号
- 0<X≤N
- 0<Y≤N
- X≠Y
Z 表示在 X、Y之间架设光纤的成本
- 0<Z<100
P 表示是否已存在光纤连接,0 表示未连接,1表示已连接
输出描述
如果给定条件,可以建设成功互联互通的5G网络,则输出最小的建设成本
如果给定条件,无法建设成功互联互通的5G网络,则输出-1
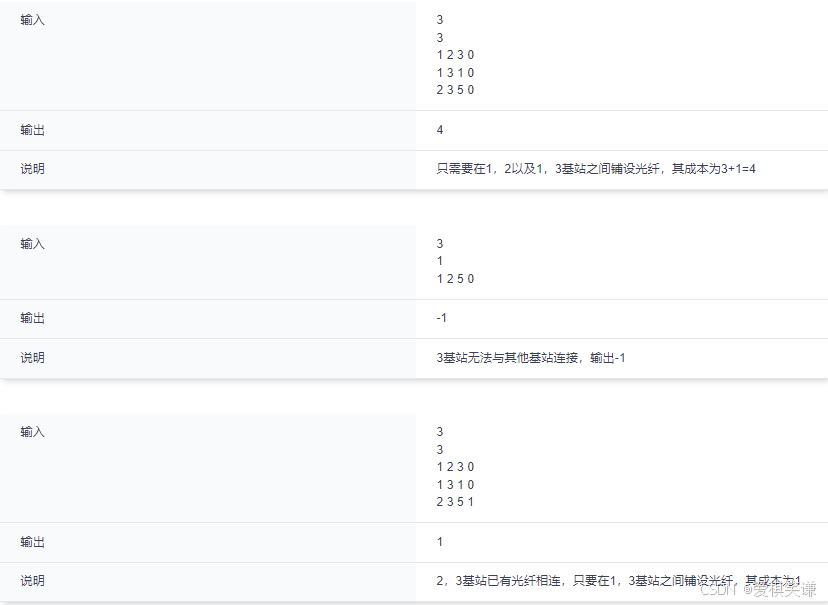
/*
3
3
1 2 3 0
1 3 1 0
2 3 5 1
*/
class Edge implements Comparable<Edge> {
int u, v, cost;
Edge(int u, int v, int cost) {
this.u = u;
this.v = v;
this.cost = cost;
}
// 用于边的排序
@Override
public int compareTo(Edge other) {
return this.cost - other.cost;
}
}
class UnionFind {
private int[] parent;
public UnionFind(int size) {
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i; // 初始化时每个节点的父节点是它自己
}
}
// 查找元素的根节点,并进行路径压缩
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 合并两个集合
public boolean union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
parent[rootY] = rootX;
return true;
}
return false;
}
}
public class G5网络建设Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt(); // 基站的个数
int M = scanner.nextInt(); // 连接的个数
List<Edge> edges = new ArrayList<>();
for (int i = 0; i < M; i++) {
int x = scanner.nextInt() - 1;
int y = scanner.nextInt() - 1;
int z = scanner.nextInt();
int p = scanner.nextInt();
if (p == 1) z = 0; // 如果已经连接,成本视为0
edges.add(new Edge(x, y, z));
}
// 按照成本从小到大排序
Collections.sort(edges);
// 使用并查集
UnionFind uf = new UnionFind(N);
int totalCost = 0;
int edgesUsed = 0;
// 遍历所有边
for (Edge edge : edges) {
if (uf.union(edge.u, edge.v)) {
totalCost += edge.cost;
edgesUsed++;
if (edgesUsed == N - 1) {
break; // 已经使用了足够的边
}
}
}
// 检查是否所有的基站都被联通
if (edgesUsed == N - 1) {
System.out.println(totalCost);
} else {
System.out.println(-1);
}
}
}