数学建模笔记—— 蒙特卡罗法

蒙特卡罗法

1. 模型原理

提出：

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”的成员S.M.乌拉姆和J.冯·诺依曼首先提出。数学家冯·诺依曼用驰名世界的赌城一摩纳哥的Monte Carlo一来命名这种方法，为它蒙上了一层神秘色彩。在这之前,蒙特卡洛方法就已经存在。1777年，法国Buffon提出用投针试验的方法求圆周率，这被认为是蒙特卡罗方法的起源。

定义：

蒙特卡罗法又称统计模拟法，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数(或更常见伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名。

原理：

由大数定理可知，当样本容量足够大时，事件的发生频率即为其概率。

注意：蒙特卡洛不是一种算法，准确的来说只是一种思想，或者是一种方法，只要求解的问题与概率模型有关联，我们就可以采用这种方法，从数学建模的角度来看，蒙特卡洛是没有通用的代码的,每个问题对应的代码都是不同的。

2. 常见问题

2.1 圆周率问题

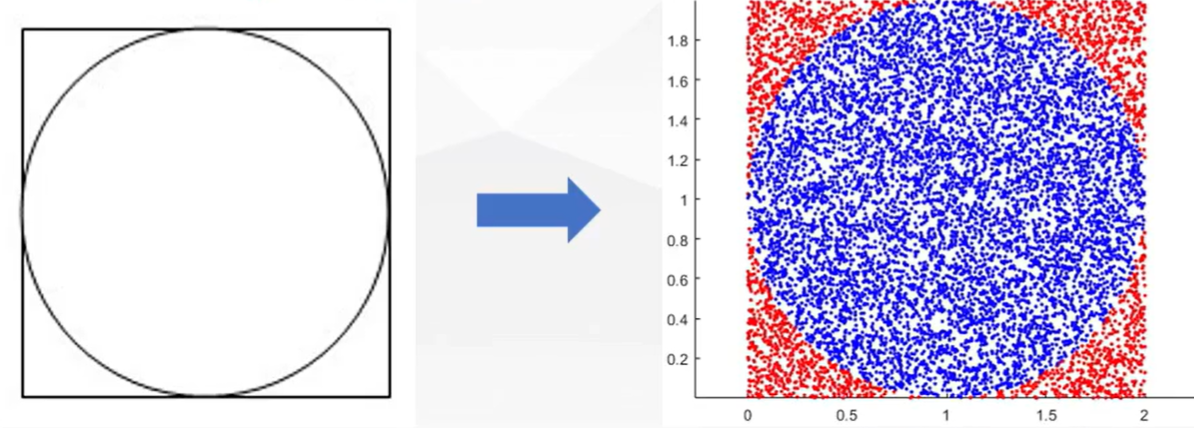
一个半径为1的圆，其外切正方形面积易知为4，若在正方形内随机撒大量的点，有些落在园内，有些落在圆外。

统计意义上：
$$\begin{gathered} \frac{圆内点数}{总点数}=\frac{圆面积}{正方形面积}=\frac{\pi }{4} \\ \pi =4\times \frac{圆内点数}{总点数} \end{gathered}$$

求解的python代码：

import numpy as np
import matplotlib.pyplot as plt

#  参数初始化，投放10000个点，圆的半径为1，圆心为(1,1)
p = 10000  # 投放点的个数
r = 1  # 圆的半径
x0, y0 = 1, 1  # 圆心的坐标
n = 0  # 初始时还未投放点，有n个点落在圆内

# 设置绘图窗口
plt.figure()
plt.title("Monte Carlo Simulation of Pi")
plt.xlabel("x")
plt.ylabel("y")

# 保持绘制窗口，多次绘图
for i in range(p):
    px = np.random.rand()*2  # 生成[0,2)之间的随机数作为点的横坐标
    py = np.random.rand()*2  # 生成[0,2)之间的随机数作为点的纵坐标

    # 判断点是否在圆内
    if (px-x0)**2+(py-y0)**2 <= r**2:
        plt.plot(px, py, '.', color='b')  # 点在圆内，蓝色
        n += 1
    else:
        plt.plot(px, py, '.', color='r')  # 点在圆外，红色
plt.axis('equal')  # 设置x,y轴的单位长度相等,保证圆不变形
plt.show()

# 计算pi的值
s = 4*n/p  # s为圆的面积，p为正方形的面积，圆的面积为pi*r^2,正方形的面积为(2r)^2
pi_estimation = s
print("Estimated pi is", pi_estimation)

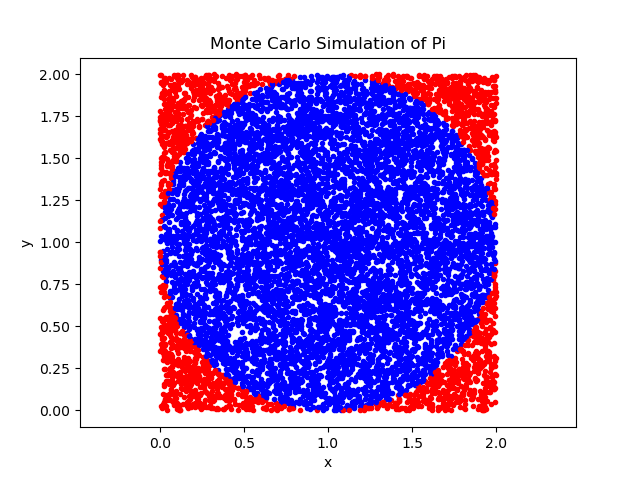
输出：

Estimated pi is 3.1416

2.2 三门问题

你参加一档电视节目，节目组提供了A、B、C三扇门，主持人告诉你，其中一扇门后边有辆汽车，其他两扇门后面是一头山羊，你可以选择一扇门打开获得门后的东西。假如你选择了B门，这时，主持人打开了C门，让你看到C门后是只山羊，然后问你要不要改选A门?(你想要汽车)

求解的python代码：

import numpy as np

n = 10000  # n代表蒙特卡罗模拟重复的次数
a = 0  # a代表不改变主意时能赢得汽车的次数
b = 0  # b代表改变主意时能赢得汽车的次数

# 重复n次蒙特卡罗模拟
for i in range(n):
    door_car_in = np.random.randint(1, 4)  # 生成1-3之间的随机数，代表汽车所在的门
    door_selected = np.random.randint(1, 4)  # 生成1-3之间的随机数，代表参赛者选择的门
    # 分两种情况讨论
    if door_car_in == door_selected:  # 如果汽车在参赛者选择的门后
        a += 1  # 不改变主意时能赢得汽车的次数加1
    else:  # 如果汽车不在参赛者选择的门后
        b += 1  # 改变主意时能赢得汽车的次数加1

print("不改变主意时能赢得汽车的概率：", a/n)
print("改变主意时能赢得汽车的概率：", b/n)

输出：

不改变主意时能赢得汽车的概率： 0.3275
改变主意时能赢得汽车的概率： 0.6725