数学建模笔记—— 模糊综合评价

模糊综合评价

1. 模糊数学概述

1965年,美国著名计算机与控制专家查德(L.A.Zadeh)教授提出了模糊的概念,并在国际期刊《Information and Control》并发表了第一篇用数学方法研究模糊现象的论文“Fuzzy Sets”(模糊集合),开创了模糊数学的新领域。

模糊是指客观事物差异的中间过渡中的“不分明性”或“亦此亦彼性”。如高个子与矮个子、年轻人与老年人、热水与凉水、环境污染严重与不严重等。在决策中,也有这种模糊的现象,如选举一个好干部,但怎样才算一个好干部?好干部与不好干部之间没有绝对分明和固定不变的界限。这些现象很难用经典的数学来描述。

模糊数学就是用数学方法研究与处理模糊现象的数学。它作为一门崭新的学科,它是继经典数学、统计数学之后发展起来的一个新的数学学科。经过短暂的沉默和争议之后,迅猛的发展起来了,而且应用越来越广泛。如今的模糊数学的应用已经遍及理、工、农、医及社会科学的各个领域,充分的表现了它强大的生命力和渗透力。统计数学是将数学的应用范围从确定性的领域扩大到了不确定性的领域,即从必然现象到偶然现象,而模糊数学则是把数学的应用范围从确定领域扩大到了模糊领域,即从精确现象到模糊现象。

实际中,我们处理现实的数学模型可以分成三大类:第一类是确定性数学模型,即模型的背景具有确定性,对象之间具有必然的关系。第二类是随机性的数学模型,即模型的背景具有随机性和偶然性。第三类是模糊性模型,即模型的背景及关系具有模糊性。

2. 经典集合和模糊集合的基本概念

2.1 经典集合

我们先来看经典集合的基本概念

• 集合：具有相同属性的事物的集体，例如：自然数集、实数集、颜色等
• 集合的基本属性：
  • 互斥性：若$a\in A,b\in A$,则$a\ne b$
  • 确定性：$a\in A,a\notin A$有且仅有之一发生(非此即彼)
• 数学上对于经典集合的刻画特征函数： f A : U → { 0 , 1 } f_A{: }U\to \{ 0, 1\} fA​:U→{0,1} $U:$论域 $f_A$表示$A$集合的特征函数
  比如$A$为成绩及格的集合，$U$为全班成绩的集合则对$\forall x\in U,f_A(x)=\{\begin{array}{l}1,x\in A\\ 0,x\notin A\end{array}$

2.2 模糊集合和隶属函数

1. 基本概念

而对于模糊集合和隶属函数来说：

• 模糊集合：用来描述模糊性概念的集合(美、丑、高、矮、年轻、年长)
• 与经典集合相比，模糊集合承认亦此亦彼
• 数学上对于模糊集合的刻画：
  隶属函数${\mu }_{{}_A}:X\to [0,1]$ (注意这里是一个区间$)x\to {\mu }_{{}_A}(x)$
  确定$X$上的一个模糊集合$A,{\mu }_A$叫做$A$的隶属函数，${\mu }_A(x)$叫做$x$对模糊集A的隶属度
  记为： A = { ( x , μ A ( x ) ) ∣ x ∈ X } A=\left\{\left(x,\mu_{A}(x)\right)|x\in X\right\} A={(x,μA​(x))∣x∈X}显然，模糊集合A完全由隶属函数来刻画${\mu }_{{}_A}(x)=0.5$最具模糊性

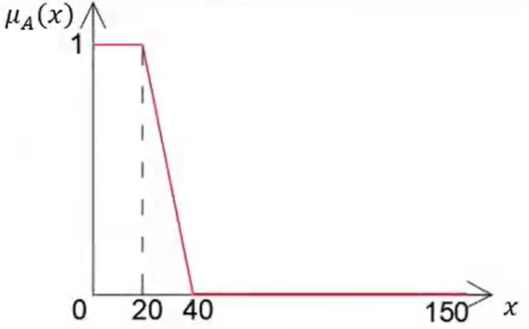
举一个简单的例子，我们要衡量“年轻”的概念 $A=$“年轻”,$X=(0,150)$表示年龄的集合
在这里我们不好直接在0-150之间画个线把年轻和不年轻区分开，我们应该给一个隶属函数来进行描述
$${\mu }_A\left(x\right)=\{\begin{array}{l}1,0<x<20\\ \frac{40-x}{20},20\le x\le 40\\ 0,40<x<150\end{array}$$

简单来说，隶属度就是某个元素属于某个模糊集合的程度，而隶属函数就是用来刻画隶属度的函数。

2.模糊集合的表示方法

当论域$X$为有限集时，记 X = { x 1 , x 2 , ⋅ ⋅ ⋅ , x n } X=\{x_1,x_2,\cdotp\cdotp\cdotp,x_n\} X={x1​,x2​,⋅⋅⋅,xn​},则$X$ 上的模糊集$A$有下列三种常见的表示形式。

1. zadeh 表示法

   当论域$X$ 为有限集时，记 X = { x 1 , x 2 , ⋯   , x n } X=\{x_1,x_2,\cdots,x_n\} X={x1​,x2​,⋯,xn​},则$X$ 上的模糊集$A$可以写成
   $$A=\sum _{i=1}^n\frac{{\mu }_A(i)}{x_i}=\frac{{\mu }_A(x_1)}{x_1}+\frac{{\mu }_A(x_2)}{x_2}+\cdots +\frac{{\mu }_A(x_n)}{x_n}$$
   注：“$\sum \text{”和“}+$”不是求和的意思，只是概括集合的记号；“$\frac{{\mu }_A(x_i)}{x_i}$”不是分数，它表示点$x_i$对模糊集$A$的隶属度是${\mu }_A(x_i)$ 。

2. 序偶表示法

$$A=\{(x_1,{\mu }_A(x_1)),(x_2,{\mu }_A(x_2)),\cdots ,(x_n,{\mu }_A(x_n))\}$$

3. 向量表示法
   $$A=({\mu }_A(x_1),{\mu }_A(x_2),\cdots ,{\mu }_A(x_n))$$

当论域$X$为无限集时，$X$上的模糊集$A$可以写成
$$A=\underset{x\in X}{\int }\frac{{\mu }_A(x)}{x}$$

注：“$\int$"也不是表示积分的意思，"$\frac{{\mu }_A(x_i)}{x_i}$”也不是分数

示例：设论域 X = { x 1 ( 140 ) , x 2 ( 150 ) , x 3 ( 160 ) , x 4 ( 170 ) , x 5 ( 180 ) , x 6 ( 190 ) } X=\{x_1(140),x_2(150),x_3(160),x_4(170),x_5(180),x_6(190)\} X={x1​(140),x2​(150),x3​(160),x4​(170),x5​(180),x6​(190)}(单位：cm)表示人的身高，$X$上的一个模糊集“高个子”($A$)的隶属函数定义为${\mu }_A(x)=\frac{x-140}{190-140}$

1. zadeh表示法
   $$A=\frac{0}{x_1}+\frac{0.2}{x_2}+\frac{0.4}{x_3}+\frac{0.6}{x_4}+\frac{0.8}{x_5}+\frac{1}{x_6}$$

2. 序偶表示法

$$A=\{(140,0),(150,0.2),(160,0.4),(170,0.6),(180,0.8),(190,1)\}$$

3. 向量表示法

$$A=(0,0.2,0.4,0.6,0.8,1)$$

3. 模糊集合的分类

模糊集合主要有三类,分别为偏小型,中间型和偏大型。其实也就类似于TOPSIS方法中的极大型、极小型、中间型、区间型指标。

举个例子,“年轻”就是一个偏小型的模糊集合,因为岁数越小,隶属度越大,就越“年轻”;“年老”则是一个偏大型的模糊集合,岁数越大,隶属度越大,越“年老”;而“中年”则是一个中间型集合,岁数只有处在某个中间的范围,隶属度才越大。总结来说,就是考虑“元素”与“隶属度”的关系,再类比一下,就是考虑隶属函数的单调性。

4. 隶属函数的确定方法

1. 模糊统计法

   模糊统计法的原理是,找多个人对同一个模糊概念进行描述,用隶属频率去定义隶属度。例如我们想知道30岁相对于“年轻”的隶属度,那就找来n个人问一问,如果其中有m个人认为30岁属于“年轻”的范畴,那m/n就可以用来作为30岁相对于“年轻”的隶属度。n越大时,走
   符合实际情况,也就越准确。这个方法比较符合实际情况,但是往往通过发放问卷或者其他手段进行调查,数学建模比赛日时间有限,所以仅做介绍,基本不予采用。

2. 借助已有的客观尺度

   对于某些模糊集合,我们可以用已经有的指标去作为元素的隶属度。例如“小康家庭”这个模糊集合,就可以用“恩格尔系数(食品支出总额/家庭总支出)”衡量相应的隶属度。显而易见,家庭越接近小康水平,其恩格尔系数应该越低,那“1-恩格尔系数”就越大,我们便可以把“1-恩格尔系数”看作家庭相对于“小康家庭”的隶属度。对于“质量稳定”这一模糊集合,我们可以使用正品率衡量隶属度。注意:隶属度是在[0,1]之间的。如果找的指标不在,可以进行归一化处理。

3. 指派法

   指派方法是一种主观的方法,它主要依据人们的实践经验来确定某些模糊集隶属函数的一种方法。

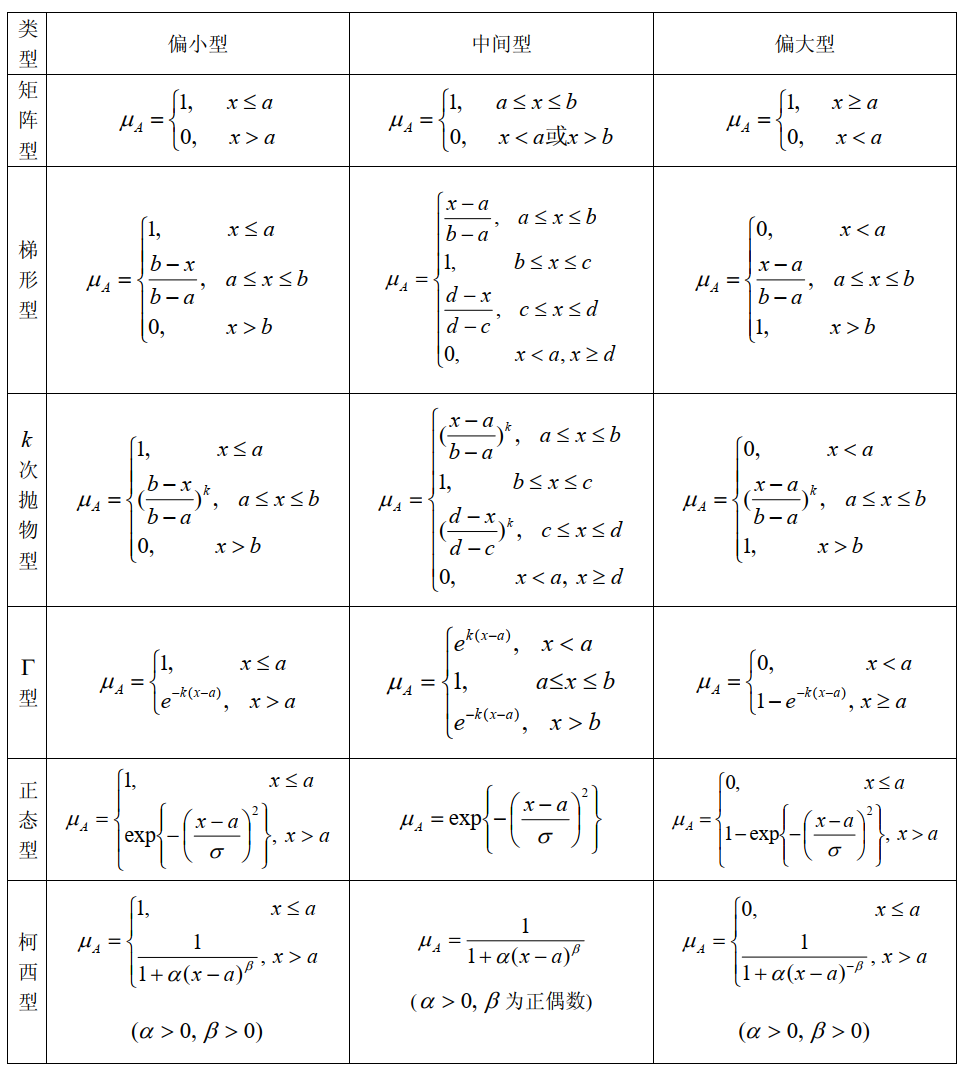
   如果模糊集定义在实数域R上,则模糊集的隶属函数称为模糊分布。所谓指派方法就是根据问题的性质主观地选用某些形式地模糊分布,再根据实际测量数据确定其中所包含地参数,常用的模糊分布如表1所示。

   实际中,根据问题对研究对象的描述来选择适当的模糊分布:

   1. 偏小型模糊分布一般适合于描述像**“小,少,浅,淡,冷,疏,青年”**等偏小的程度的模糊现象。

   2. 偏大型模糊分布一般适合于描述像**“大,多,深,浓,热,密,老年”**等偏大的程度的模糊现象。

   3. 中间型模糊分布一般适合于描述像**“中,适中,不太多,不太少,不太深,不太浓,暖和,中年”**等处于中间状态的模糊现象。

   但是,表1给出的隶属函数都是近似的,应用时需要对实际问题进行分析,逐步修改进行完善,最后得到近似程度更好的隶属函数。

3. 评价问题概述

模糊评价问题是要把论域中的对象对应评语集中一个指定的评语或者将方案作为评语集并选择一个最优的方案。

在模糊综合评价中，引入三个集合：

1. 因素集(评价指标集) U = { u 1 , u 2 , ⋯   , u n } U=\{u_1,u_2,\cdots,u_n\} U={u1​,u2​,⋯,un​}

2. 评语集(评价的结果) V = { v 1 , v 2 , ⋯   , v n } V= \{ v_1, v_2, \cdots , v_n\} V={v1​,v2​,⋯,vn​}

3. 权重集(指标的权重) $A=\left\{\begin{array}{c}{a}_1,a_2,\cdot \cdot \cdot ,a_n\end{array}\right\}$

例：评价一名学生的表现
U = { U=\{ U={专业排名、课外实践、志愿服务、竞赛成绩$\}$
V = { V=\{ V={优、良、差$\}$
A = { 0.4 、 0.2 、 0.1 、 0.3 } A=\{0.4、0.2、0.1、0.3\} A={0.4、0.2、0.1、0.3}

模糊综合评价模型就是给定对象，用因素集的指标进行评价，从评语集中找到一个最适合它的评语。如果评语集中是方案的话，就是选出一个最恰当的方案。这种“合适”就是隶属度，隶属于某个模糊集合的程度。

4. 一级模糊综合评价模型

在对企业员工进行考核时，在指标个数较少的考核中，可以运用一级模糊综合评判。

1. 确定因素集：评判的因素构成的评价指标体系集合称为因素集
   对员工的表现，需要从多个方面进行综合评判，如员工的工作业绩、工作态度、沟通能力、政治表现等。记为 U = { u 1 , u 2 , ⋯   , u n } U=\{u_1,u_2,\cdots,u_n\} U={u1​,u2​,⋯,un​}，

   这里取因素集 U = { 政治表现 u 1 , 工作能力 u 2 , 工作态度 u 3 , 工作成绩 u 4 } U=\{政治表现u_1,工作能力u_2,工作态度u_3,工作成绩u_4\} U={政治表现u1​,工作能力u2​,工作态度u3​,工作成绩u4​}

2. 确定评语集：由各种不同决断构成的集合称为评语集
   评价往往有不同的等级，对员工评价可能有好、较好、中等、较差、很差等记为 V = { v 1 , v 2 , . . . , v n } V= \{ v_1, v_2, . . . , v_n\} V={v1​,v2​,...,vn​}

   这里取评语集 V = { 优秀 v 1 , 良好 v 2 , 一般 v 3 , 较差 v 4 , 差 v 5 } V=\{优秀v_1,良好v_2,一般v_3,较差v_4,差v_5\} V={优秀v1​,良好v2​,一般v3​,较差v4​,差v5​}

3. 确定各因素的权重：因素集中各因素的评价中作用不同，需要确定权重，它是$U$上的模糊向量
   判断权重的方法很多，如Delphi法等，也可以用我们学习过的层次分析法和熵权法来确定权重
   记为 $A=[a_1,a_2,...,a_n]$

   这里取 $A=[0.25,0.2,0.25,0.3]$

4. 确定模糊综合判断矩阵

   对指标$u_i$来说，对各个评语的隶属度为V上的模糊子集，对指标$u_i$的评判记为记为$R_i=[r_{i1},r_{i2},...,r_{in}]$ 各指标的模糊综合判断矩阵为
   $$R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{nm}\end{array}\right]$$
   这是一个从$U$到$V$的模糊关系矩阵。对员工的评定如果由模糊统计法来确定：

   1. $u_1$比如由群众打分确定
      $$r_1=[0.1,0.5,0.4,0,0]$$
      上式表示，参与打分的群众中，10%的人认为该员工政治表现优秀，50%的人认为其政治表现良好等

   2. $u_2,u_3$由部门领导打分来确定
      $$\begin{gathered} r_3=[\begin{array}{c}0.2,0.5,0.3,0,0\end{array}] \\ {r}_2=[0.2,0.5,0.2,0.1,0] \end{gathered}$$

   3. $u_4$由单位考核组成员打分来确定
      $$r_4=[0.2,0.6,0.2,0,0]$$
      形成以$R_i$为第$i$行构成评价矩阵(模糊综合判断矩阵)
      $$R=\left[\begin{array}{ccccc}0.1& 0.5& 0.4& 0& 0\\ 0.2& 0.5& 0.2& 0.1& 0\\ 0.2& 0.5& 0.3& 0& 0\\ 0.2& 0.6& 0.2& 0& 0\end{array}\right]$$

5. 模糊综合评判，进行矩阵合成运算

   选择评价的合成算子，将$A$与$R$ 合成得到 $B=(b_1,b_2,\cdots ,b_m)$
   $$\begin{gathered} B=A\mathrm{O}R=(a_1,a_2,\cdots ,a_n)\mathrm{O}\left(\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ \cdots & \cdots & \cdots & \cdots \\ & & & \\ r_{n1}& r_{n2}& \cdots & r_{nm}\end{array}\right) \\ {b}_j=(a_1\bullet r_{1j})+(a_2\bullet r_{2j})+\cdots +(a_n\bullet r_{nj}),j=1,2,\cdots ,m \end{gathered}$$

   常用的模糊算子有：

   1. $M(\wedge ,\vee )$, 即用$\wedge$代替$\bullet$,用$\vee$代替+,式中$\wedge$为取小运算，$\vee$代表取大运算
      2. $M(\bullet ,\vee )$ , 即用实数乘法$\bullet$代替$\bullet$,用$\vee$代替$+$
      3. $M(\wedge ,\oplus )$,即用$\wedge$代替$\bullet$,用$\oplus$代替+,其中$a\oplus b=\min (1,a+b)$ ;
      4. $M(\bullet ,\oplus )$ , 即用实数乘法$\bullet$代替$\bullet$,用$\oplus$代替+。
      经过比较研究，$M(\bullet ,\oplus )$对各因素按权数大小，统筹兼顾，综合考虑，比较合理。

   $$B=A\cdot R=[0.25,0.2,0.25,0.3]\cdot \left[\begin{array}{ccccc}0.1& 0.5& 0.4& 0& 0\\ 0.2& 0.5& 0.2& 0.1& 0\\ 0.2& 0.5& 0.3& 0& 0\\ 0.2& 0.6& 0.2& 0& 0\end{array}\right]=[0.175,0.53,0.275,0.02,0]$$

   取数值最大的评语作为综合评判结果，即评判结果为“良好”。

典型例题

例：某露天煤矿有五个边坡设计方案，其各项参数根据分析计算结果得到边坡设计方案如下表

项目	方案1	方案2	方案3	方案4	方案5
可采矿量/万吨	4700	6700	5900	8800	7600
基建投资/万元	5000	5500	5300	6800	6000
采矿成本/(元/吨)	4.0	6.1	5.5	7.0	6.8
不稳定费用/万元	30	50	40	200	160
净现值/万元	1500	700	1000	50	100

据勘探，该矿探明储量8800吨，开采总投资不超过8000万元，试做出各方案的优劣排序，选出最佳方案

1. 首先确定可采矿量的隶属函数

   因为勘探的储量为8800吨，故可用资源的利用函数作为隶属函数
   $${\mu }_A(x)=\frac{x}{8800}$$

2. 基建投资的隶属函数

   投资约束是8000万元，所以
   $${\mu }_B\left(x\right)=1-\frac{x}{8000}$$

3. 采矿成本的隶属函数

​ 根据专家意见，采矿成本$a_1\le 5.5$元/吨为低成本，$a_2=8.0$元/吨为高成本，故
$${\mu }_c\left(x\right)=\{\begin{array}{ll}1,& 0\le x\le a_1\\ \frac{a_2-x}{a_2-a_1},& a_1\le x\le a_2\\ 0,& a_2<x\end{array}$$

4. 不稳定费用的隶属函数
   $${\mu }_D\left(x\right)=1-\frac{x}{200}$$

5. 净现值的隶属函数

   取上限15(百万元),下限0.5(百万元),采用线性隶属函数

   $${\mu }_E\left(x\right)=\frac{x-50}{1500-50}=\frac{x-50}{1450}$$

6. 根据各个隶属函数计算出5个方案所对应的不同隶属度

   项目	方案1	方案2	方案3	方案4	方案5
   可采矿量/万吨	0.5341	0.7614	0.6705	1	0.8636
   基建投资/万元	0.3750	0.3125	0.3375	0.15	0.25
   采矿成本/(元/吨)	1	0.76	1	0.4	0.48
   不稳定费用/万元	0.85	0.75	0.8	0	0.2
   净现值/万元	1	0.4480	0.6552	0	0.0345

   确定单因素评判矩阵

$$\begin{array}{r}R=\left[\begin{array}{ccccc}0.5341& 0.7614& 0.6705& 1.0000& 0.8636\\ 0.3750& 0.3125& 0.3375& 0.1500& 0.2500\\ 0.8500& 0.7500& 0.8000& 0.0000& 0.2000\\ 1.0000& 0.7600& 1.0000& 0.4000& 0.4800\\ 1.0000& 0.4480& 0.6552& 0.0000& 0.0345\end{array}\right]\end{array}$$

​ 根据专家评价，诸因素在决策中占的权重为$A=(0.25,0.20,0.20,0.10,0.25)$
​ 注：没有专家可以用熵权法、层次分析法等

7. 综合评价

​ $B=A\cdot R=(0.7435,0.5919,0.6789,0.3600,0.3905)$
​ 由此可知：方案1最佳，方案3次之，方案4最差

5. 多层次模糊综合评价模型

多层次综合评价模型的解题步骤如下

1. 给出被评价的对象集合 X = { x 1 , x 2 , . . . , x k } X=\{x_1,x_2,...,x_k\} X={x1​,x2​,...,xk​}

2. 确定因素集(亦称指标体系) U = { u 1 , u 2 , . . . , u n } U=\{u_1,u_2,...,u_n\} U={u1​,u2​,...,un​}

   若因素众多，往往将 U = { u 1 , u 2 , . . . , u n } U=\{u_1,u_2,...,u_n\} U={u1​,u2​,...,un​}按某些属性分成s个子集

​ $U_i=\left\{u_1^{(i)},u_2^{(i)},...,u_{n_i}^{(i)}\right\}$, $i=1,2,...,s$且满足条件：

​ ①${\sum }_{i=1}^s{n}_i=n;$ ②${\bigcup }_{i=1}^s{U}_i=U;$ ③$U_i\bigcap U_j=\varphi ,i\ne j$

3. 确定评语集 V = { v 1 , v 2 , . . . , v m } V=\{v_1,v_2,...,v_m\} V={v1​,v2​,...,vm​}

4. 由因素集$U_i$与评语集$V$,可获得一个评价矩阵
   $$R_i=\left[\begin{array}{cccc}{r}_{11}^{(i)}& r_{12}^{(i)}& ...& r_{1m}^{(i)}\\ ⋮& ⋮& ⋮& ⋮\\ r_{n_{i}1}^{(i)}& r_{n_{i}2}^{(i)}& ...& r_{n_{i}m}^{(i)}\end{array}\right]$$

5. 对每一个$U_i$，分别作出综合决策。

   设$U_i$中的各因素权重的分配(模糊权向量)为$A_i=\left(a_1^{(i)},a_2^{(i)}\dots ,a_{n_i}^{(i)}\right)$, 其中${\sum }_{t=1}^{n_i}{a}_t^{(i)}=1$。

   若$R_i$为单因素模糊判断矩阵，则得到一级评价向量为：

​ $B_i=A_i\cdot R_i=(b_{i1},b_{i2},...,b_{im})$, $i=1,2,...,s$

6. 将每个$U_i$视为一个元素，记 U = { U 1 , U 2 , . . . , U s } U=\{U_1,U_2,...,U_s\} U={U1​,U2​,...,Us​}, 于是$U$又是单因素集，$U$的单因素判断矩阵为
   $$R=\left[\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_s\end{array}\right]=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1m}\\ ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮\\ b_{s1}& b_{s2}& \cdots & b_{sm}\end{array}\right]$$
   每个$U_i$作为$U$的一部分，反映了$U$的某种属性，可以按他们的重要性给出权重分配
   $$A=(a_1,a_2,...,a_s)$$
   于是得到二级模糊综合评价模型为：
   $$B=A\cdot R=(b_1,b_2,...,b_m)$$
   若每个子因素$U_i(i=1,2,...,s)$仍有较多因素，则可将$U_i$再划分，于是有三级或更高级模型

典型例题

对某陶瓷厂生产的6种产品的销售前景进行评判

1. 影响评判对象因素集的选取
   从产品情况、销售能力、市场需求三个方面考虑,根据专家评判法,得到评判对象因素集及子因素组成下图,因素后面数据表示权重

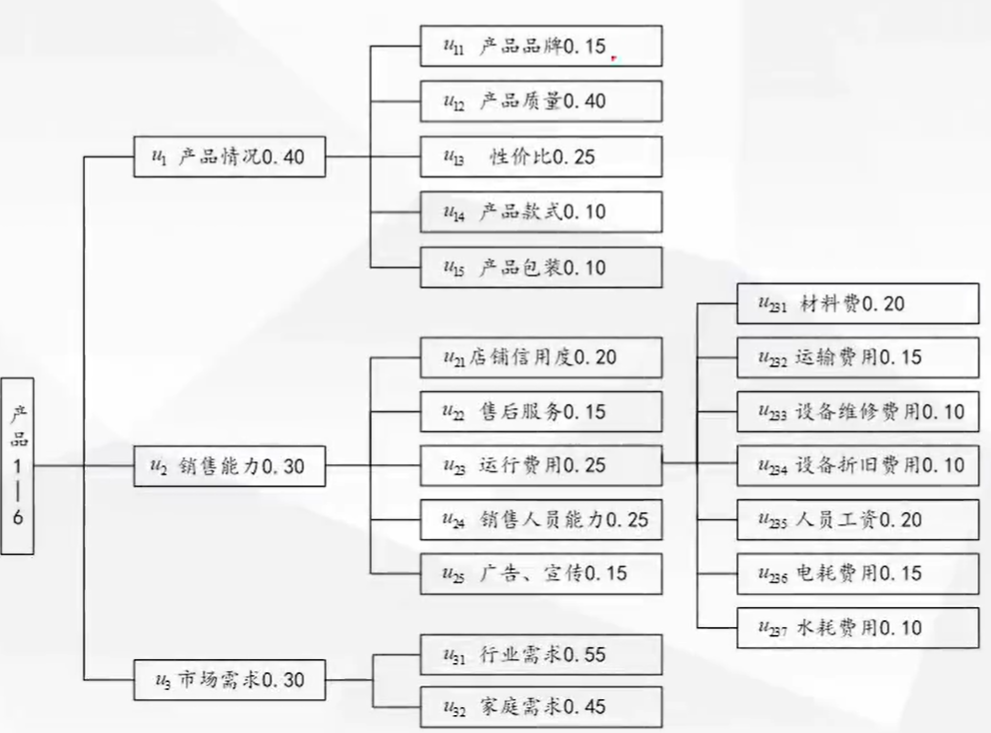
2. 备择集 V = { 1 , 2 , 3 , 4 , 5 , 6 } V=\{1,2,3,4,5,6\} V={1,2,3,4,5,6}代表6种不同的陶瓷产品

3. 一级模糊综合评价

   “运行费用”下属的三级指标是定量指标，有具体数据，对这些数据归一化即求出各种产品的该指标与总指标的比重，得到单因素隶属度；由于其他因素均为定性指标，通过市场调查，把消费者的满意度作为单因素的隶属度，6种产品的单因素隶属度如下表：

   因素	产品1	产品2	产品3	产品4	产品5	产品6
   $u_{11}$产品品牌	0.12	0.18	0.17	0.23	0.13	0.17
   $u_{12}$产品质量	0.15	0.13	0.18	0.25	0.12	0.17
   $u_{13}$性价比	0.14	0.13	0.16	0.18	0.20	0.19
   $u_{14}$产品款式	0.12	0.14	0.15	0.17	0.19	0.23
   $u_{15}$ 产品包装	0.16	0.12	0.13	0.25	0.18	0.16
   $u_{21}$ 店铺信用度	0.13	0.15	0.14	0.18	0.16	0.24
   $u_{22}$售后服务	0.12	0.16	0.13	0.17	0.19	0.23
   $u_{231}$材料费	0.18	0.14	0.18	0.14	0.13	0.23
   $u_{232}$运输费用	0.15	0.2	0.15	0.25	0.1	0.15
   $u_{233}$设备维修费用	0.25	0.12	0.13	0.12	0.18	0.2
   $u_{234}$设备折旧费用	0.16	0.15	0.21	0.11	0.2	0.17
   $u_{235}$人员工资	0.23	0.18	0.17	0.16	0.15	0.11
   $u_{236}$电耗费用	0.19	0.13	0.12	0.12	0.11	0.33
   $u_{237}$水耗费用	0.17	0.16	0.15	0.08	0.25	0.19
   $u_{24}$销售人员能力	0.14	0.13	0.15	0.16	0.18	0.24
   $u_{25}$广告宣传	0.16	0.15	0.15	0.17	0.18	0.19
   $u_{31}$行业需求	0.15	0.14	0.13	0.18	0.14	0.26
   $u_{32}$家庭需求	0.16	0.15	0.18	0.14	0.16	0.21

   影响运行费用的各因素的单因素评价矩阵为：
   $$\begin{array}{c}{R}_{23}=\left[\begin{array}{cccccc}0.18& 0.14& 0.18& 0.14& 0.13& 0.23\\ 0.15& 0.20& 0.15& 0.25& 0.10& 0.15\\ 0.25& 0.12& 0.13& 0.12& 0.18& 0.20\\ 0.16& 0.15& 0.21& 0.11& 0.20& 0.17\\ 0.23& 0.18& 0.17& 0.16& 0.15& 0.11\\ 0.19& 0.13& 0.12& 0.12& 0.11& 0.33\\ 0.17& 0.16& 0.15& 0.08& 0.25& 0.19\end{array}\right]\end{array}$$
   权重分配为：$A_{23}=\left[\begin{array}{ccccccc}0.20& 0.15& 0.10& 0.10& 0.20& 0.15& 0.10\end{array}\right]$，则运行费用的一级评判为：

   $B_{23}=A_{23}\bullet R_{23}=\left[\begin{array}{cccccc}0.1910& 0.1565& 0.1595& 0.1465& 0.1505& 0.1960\end{array}\right]$

4. 二级模糊综合评判

   对产品情况、销售能力、市场需求下属的单因素指标进行二级评判

   产品情况的二级评判如下：
   $$\begin{gathered} R_1=\left[\begin{array}{cccccc}0.12& 0.18& 0.17& 0.23& 0.13& 0.17\\ 0.15& 0.13& 0.18& 0.25& 0.12& 0.17\\ 0.14& 0.13& 0.16& 0.18& 0.20& 0.19\\ 0.12& 0.14& 0.15& 0.17& 0.19& 0.23\\ 0.16& 0.12& 0.13& 0.25& 0.18& 0.16\end{array}\right] \\ \begin{array}{rl}& A_1=\left[\begin{array}{ccccc}0.15& 0.40& 0.25& 0.10& 0.10\end{array}\right]\\ & B_1=A_1\bullet R_1=\left[\begin{array}{cccccc}0.1410& 0.1375& 0.1655& 0.2215& 0.1545& 0.1800\end{array}\right]\end{array} \end{gathered}$$
   将运行费用的一级评判结果作为二级评判的单因素评价值，即评判矩阵的第三行，则销售能力的评判如下
   $$\begin{gathered} R_2=\left[\begin{array}{cccccc}0.13& 0.15& 0.14& 0.18& 0.16& 0.24\\ 0.12& 0.16& 0.13& 0.17& 0.19& 0.23\\ 0.1910& 0.1565& 0.1595& 0.1465& 0.1505& 0.1960\\ 0.14& 0.13& 0.15& 0.16& 0.18& 0.24\\ 0.16& 0.15& 0.15& 0.17& 0.18& 0.19\end{array}\right] \\ \begin{array}{rl}& A_2=\left[\begin{array}{ccccc}0.20& 0.15& 0.25& 0.25& 0.15\end{array}\right]\\ & B_2=A_2•R_2=\left[\begin{array}{cccccc}0.1508& 0.1481& 0.1474& 0.1636& 0.1701& 0.2200\end{array}\right]\end{array} \end{gathered}$$
   市场需求的评判如下：
   $$\begin{array}{rl}& R_3=\left[\begin{array}{cccccc}0.15& 0.14& 0.13& 0.18& 0.14& 0.26\\ 0.16& 0.15& 0.18& 0.14& 0.16& 0.21\end{array}\right]\\ & A_3=\left[\begin{array}{cc}0.55& 0.45\end{array}\right]\\ & B_3=A_3•R_3=\left[\begin{array}{cccccc}0.1545& 0.1445& 0.1525& 0.1620& 0.1490& 0.2375\end{array}\right]\end{array}$$

5. 三级模糊综合评价

   将二级评判结果$B_1,B_2,B_3$作为行，组成三级评判的单因素评判矩阵

   $R=\left[\begin{array}{c}{B}_1\\ B_2\\ B_3\end{array}\right]$

   权重及$A=[0.40$ 0.30 0.30]

   $B=A\cdot R=[0.1480$ 0.1428 0.1562 0.1863 0.1575 0.2093]

   由结果可知，产品6得分最高，可加大投资，产品1、2得分较低，应减少投资

6. python实现

import numpy as np

# 1. 一级模糊综合评判
# 定义单因素评价矩阵
R23 = np.array(
    [[0.18, 0.14, 0.18, 0.14, 0.13, 0.23],
     [0.15, 0.20, 0.15, 0.25, 0.10, 0.15],
     [0.25, 0.12, 0.13, 0.12, 0.18, 0.20],
     [0.16, 0.15, 0.21, 0.11, 0.20, 0.17],
     [0.23, 0.18, 0.17, 0.16, 0.15, 0.11],
     [0.19, 0.13, 0.12, 0.12, 0.11, 0.33],
     [0.17, 0.16, 0.15, 0.08, 0.25, 0.19],]
)
# 权重分配向量
A23 = np.array([0.20, 0.15, 0.10, 0.10, 0.20, 0.15, 0.10])
# 评价结果
# np.dot是numpy中的矩阵乘法函数，计算两个矩阵的内积
B23 = np.dot(A23, R23)

# 2. 二级模糊综合评判
# 产品情况的二级评判如下
R1 = np.array(
    [[0.12, 0.18, 0.17, 0.23, 0.13, 0.17],
     [0.15, 0.13, 0.18, 0.25, 0.12, 0.17],
     [0.14, 0.13, 0.16, 0.18, 0.20, 0.19],
     [0.12, 0.14, 0.15, 0.17, 0.19, 0.23],
     [0.16, 0.12, 0.13, 0.25, 0.18, 0.16]]
)
# 权重分配向量
A1 = np.array([0.15, 0.40, 0.25, 0.10, 0.10])
# 评价结果
B1 = np.dot(A1, R1)
# 销售能力的二级评判如下
R2 = np.array(
    [[0.13, 0.15, 0.14, 0.18, 0.16, 0.25],
     [0.12, 0.16, 0.13, 0.17, 0.19, 0.23],
     B23,
     [0.14, 0.13, 0.15, 0.16, 0.18, 0.24],
     [0.16, 0.15, 0.15, 0.17, 0.18, 0.19]]
)
A2 = np.array([0.2, 0.15, 0.25, 0.25, 0.15])
B2 = np.dot(A2, R2)
# 市场需求的二级评判如下
R3 = np.array(
    [[0.15, 0.14, 0.13, 0.18, 0.14, 0.26],
     [0.16, 0.15, 0.18, 0.14, 0.16, 0.21]]
)
A3 = np.array([0.55, 0.45])
R3 = np.dot(A3, R3)

# 3. 三级模糊综合评判
R = np.array([B1, B2, R3])
A = np.array([0.4, 0.3, 0.3])
B = np.dot(A, R)
print("产品的综合评价值为：", B)

输出：

产品的综合评价值为： [0.147975  0.1427875 0.1561625 0.1862875 0.1575375 0.20985  ]