数据结构算法——排序算法
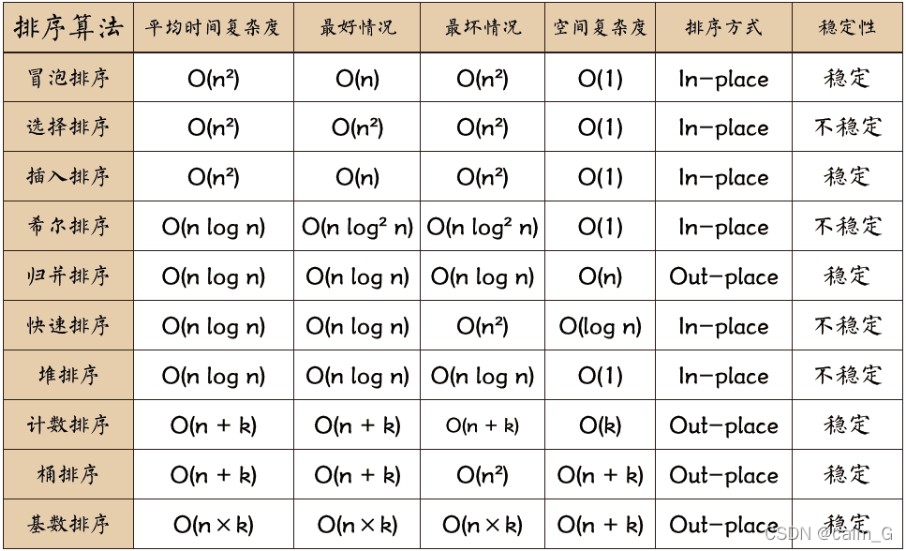
1.排序
1.选择排序
不稳定,一般不用,基本排序
思路:过滤数组,找到最小数,放在前面。
不稳:导致原本在前的数据移动到后面。
int arr[];
for(i=0;i<arr.length-1;i++){
int smallest=i;
for(j=i+1;j<length;j++){
if(arr[j]<arr[smallest]){
smallest=j;
}
swap(arr,i,smallest);
}
}
时间复杂度O(n2),空间复杂度O(1)
2.冒泡排序
稳定,不常用,太慢,基本排序
思路:从第一个数两两比较,然后大的向后交换位置。
int arr[];
for(i=arr.length-1;i>0;i--){
for(j=0;j<i;j++){
if(arr[j]>arr[j+1]){
swap[arr,j,j+1]
}
}
}
时间复杂度O(n2),空间复杂度O(1)
3.插入排序
稳定,三种基本排序中最常用,在数据较少且有一定次序时效率很高
思路:从第二位向后过滤,向前逐位比较并与更小的交换直到大于或等于。
int arr[];
for(i=1;i<arr.length-1;i++){
for(j=i;i>0;i--){
if(arr[j-1]>arr[j]) swap(arr,j-1,j);
}
}
时间复杂度O(n2),空间复杂度O(1)
4.希尔排序
稳定,是优化过的插入排序
思路:按一定数据间隔将数据分组进行插入排序,然后缩小间隔进行,直到为1。
问:为什么比插入排序更优?
答:分组大时,换位次数少。分组小时,换位距离短。
int arr[];
int h=1;
while(h<=arr.length/3){
h=h*3+1; //计算Knuth数列
}
for(gap=h;gap>0;gap=(gap-1)/3){ //缩小间隔
for(i=gap;i<arr.length;i++){
for(j=i;j>gap-1;j-=gap){
if(arr[j-gap]>arr[j]) swap(arr,j-gap,j); //每组进行插入排序
}
}
时间复杂度O(n^1.3),空间复杂度O(1)
5.归并排序
稳定,对于预先有一定次序的数组效率很高
思路:将数组递归地分为两部分,然后两个部分中的数依次比较,较小的填入中间数组。
public void sort(int[] arr,left,right){
if(left==right) return; //边界判定,何时停止
int mid=left-(left+right)/2; //递归中点计算
sort(arr,left,mid); //左侧递归
sort(arr,mid+1,right); //右侧递归
merge(arr,left,mid,right); //进行分组排序
print(arr);
}
public void merge(int[] arr,leftPtr,rightPtr,rightBound){
int temp[]=new int[leftPtr-rightBound+1]; //定义中间数组
int i=leftPtr; //定义左指针,右指针
int j=rightPtr;
int k=-1;
while(i<rightPtr&&j<rightBound){
temp[k++] = arr[i] <= arr[j] ? arr[++i] : arr[++j]; //将左指针和右指针指向的数小的放入中间数组
}
while(i<rightPtr-1) temp[k++]=arr[i++]; //将左侧剩余数放入中间数组
while(j<rightBound) temp[k++]=arr[j++]; //将右侧剩余数放入中间数组
for(int m=0;m<temp.length;m++) arr[leftPtr+m]=temp[m]; //将中间数组放入原数组
}
时间复杂度O(N log N),空间复杂度O(N)
6.快速排序
不稳
原理:选出一个数,将比它小的数放到它左侧,比它大的数放到它右侧。
可优化位双轴快速排序(java中对较大数组的排序方法)
/*
*@param left 左边界
*@param right 右边界
*/
public void sort(arr[],left,right){
//边界判断
if(left>=right) return;
//初始化左右指针
int i=left;
int j=right;
//将最后一位定为pivot
int pivot=arr[right];
while(i<j){
//如果左侧比pivot大,则与右侧比pivot小的换位
while(arr[i]<=pivot) i++;
while(arr[j]>pivot) j--;
//如果左指针大于等于右指针说明本次排序结束
if(i>=j) break;
swap(arr,i,j);
}
if(arr[i]<=pivot){
swap(arr,i+1,right); //将pivot放在中间,此时,左侧比pivot小,右侧比pivot大
}else{
swap(arr,i,right);
}
sort(arr[],left,i-1); //左侧递归
sort(arr[],i,right); //右侧递归
}
时间复杂度O(N log N),空间复杂度O(1)
7.计数排序
桶排序的一种,非比较排序,稳定(优化后),对于数量大但数据大小数量少的情况效率很高
思路:将每种数据的数量放入中间数组中,然后按放回原数组中。
int arr[];
//进行取数组最大值,最小值的步骤,在此处省略,并初始化min,max为最小最大值
int max;
int min;
sort(arr,max,min){
int count=new int[max-min+1]; //设置计数桶
int temp[arr.length]; //初始化中间数组
for(i=0;i<arr.length;i++){
count[arr[i]-min]++; //计数
}
for(j=0;j<count.length;j++){
count[j+1]+=count[j]; //优化步骤,此时桶中存储的是该数据最后一位的位置
}
for(k=arr.length;k>=0;k--){
temp[--count[ arr[k]-min ]] = arr[k]; //优化步骤,从原数组最后开始过滤,将数据放到对应位置
}
return temp;
}
时间复杂度O(N+K),空间复杂度O(N+K) (K是计数桶大小)
8.基数排序
桶排序的一种,非比较排序,基于技术排列,稳定
思路:对数据每一位上进行计数排列
从最低位开始的基数排序
int arr[];
//对最高位进行计算,此处跳过此步骤,直接初始化变量h为最高位数
int h;
sort(arr,h){
int count=new int[10]; //设置计数桶,此时只有0-9
int temp[arr.length]; //初始化中间数组
for(m=0;m<h;m++){
int divison=(int)Math.pow(10,m); //求10的m次幂
for(i=0;i<arr.length;i++){
count[arr[i]/divison%10]++; //计数
}
for(j=0;j<count.length-1;j++){ //优化步骤,此时桶中存储的是该数据最后一位的位置
count[j+1]+=count[j];
}
for(k=arr.length;k>=0;k--){ //优化步骤,从原数组最后开始过滤,将数据放到对应位置
temp[--count[arr[k]]]=arr[k];
}
}
return temp;
}
从最高位开始的基数排序
递归思想
int arr[];
//对最高位进行计算,此处跳过此步骤,直接初始化变量h为最高位数
int h;
sort(arr,h){
if(h=1) return temp;
int divison=(int)Math.pow(10,h); //求10的i次幂
int count=new int[10]; //设置计数桶,此时只有0-9
int temp[arr.length]; //初始化中间数组
for(i=0;i<arr.length;i++){
count[arr[i]/divison%10]++; //计数
}
for(j=0;j<count.length-1;j++){ //优化步骤,此时桶中存储的是该数据最后一位的位置
count[j+1]+=count[j];
}
sort(arr,h-1);
for(k=arr.length;k>=0;k--){ //优化步骤,从原数组最后开始过滤,将数据放到对应位置
temp[--count[arr[k]]]=arr[k];
}
}
时间复杂度O(N_K),空间复杂度O(N_K) (K是计数桶大小)
9.桶排序
不常用,效率低
思路:将数据区域分为几个“桶”,将数据放入对应的“桶”中,对每个桶进行排序(其他排序方法或者递归)。
10.堆排序
堆排序是利用堆这种数据结构设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(NlogN),不稳定
思路:将数组转换成一个堆(视情况使用大顶堆或者小顶堆,此处为大顶堆),将最大值下沉(第一位和最后一位换位),将其他位数转换成堆,直到数组有序。
public static void heapSort(int arr[]) {
int temp = 0;
for(int i = arr.length / 2 -1; i >=0; i--) {
adjustHeap(arr, i, arr.length);
}
for(int j = arr.length-1;j >0; j--) {
swap(i,j);
adjustHeap(arr, 0, j);
}
}
//将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
* @param arr 待调整的数组
* @param ptr 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int ptr, int length) {
// k = ptr * 2 + 1 k 是 ptr 结点的左子结点
for(int k = ptr * 2 + 1; k < length; k = k * 2 + 1) {
//判断,避免遍历左右子树
if(k+1 < length && arr[k] < arr[k+1]) { //如果左子节点比右子节点小,则转向右子节点
k++;
}
//子节点判断
if(arr[k] > arr[ptr]) {
swap(arr,ptr,j)
ptr = k; //对子树进行调整,避免结构混乱
} else {
break;
}
}
}
时间复杂度 O(N*Log N),空间复杂度O(1)
