数据结构——查找算法

查找

1.线性查找

思路：从一侧遍历。

	for(i=0;i<length-1;i++){
        if(arr[i]=key) return i;
    }
	return -1;

2.二分查找

是一种对一个有序数组查询的方法

思路：先和中位数比较，大于中位数则向右便利，小于中位数则向左遍历

找单个数下标实现：

	int mid=(left+right)/2;
	if(left>=right) return -1;
	if(key>arr[mid]){
        for(i=mid;i<right;i++){
            return arr[i]==key?i:-1;
        }
    }else if(key<arr[mid]){
        for(i=mid;i>=left;i--){
            return arr[i]==key?i:-1;
        }else{
            return mid;
        }
    }

找多个数下标：

	List<Integer> result;
	int mid=(left+right)/2;
	if(left>=right) return -1;
	if(key==arr[mid]) result.add(mid);
	for(i=mid+1;i<right;i++){
        if(key==arr[i]) result.add(i);
        if(key>arr[i]) break;
    }
	for(i=mid-1;i>left;i++){
        if(key==arr[i]) result.add(i);
        if(key<arr[i]) break;
    }
	return result;

3.二分查询 （递归）

	public List<int> binarySearch(int[] arr,int target){
        List<int> result = new List<int>;
        if(arr.length==0) throw arraySizeError; 
        binarySearch(arr,result,0,arr.length-1,target)
    }
	public List<int> binarySearch(int[] arr,List<int> result,int left,int right,int target){
        if(left>right) return result;
        int mid = right - (left+right)/2;
        if(arr[mid]==target) result.add[mid];
        if(arr[mid]<target) binarySearch(arr,result,mid,right,target);
        if(arr[mid]>target) binarySearch(arr,result,left,mid,target);
        return result;
    }

4.插值查找

对于数据量较大，关键字分布比较均匀的查找表来说，采用插值查找，速度较快

关键字分布不均匀的情况下，该方法不一定比二分查找要好

思路：类似于二分查找，但是mid中点不是数组中点，而是 mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) ;

找单个数下标实现：

	int mid = left + (right - left) * (key - arr[left]) / (arr[right] - arr[left]) ;
	if(left>=right) return -1;
	if(key>arr[mid]){
        for(i=mid;i<right;i++){
            return arr[i]==key?i:-1;
        }
    }else if(key<arr[mid]){
        for(i=mid;i>=left;i--){
            return arr[i]==key?i:-1;
        }else{
            return mid;
        }
    }

找多个数下标：

	List<Integer> result;
	int mid = left + (right - left) * (key - arr[left]) / (arr[right] - arr[left]) ;	
	if(left>=right) return -1;
	if(key==arr[mid]) result.add(mid);
	for(i=mid+1;i<right;i++){
        if(key==arr[i]) result.add(i);
        if(key>arr[i]) break;
    }
	for(i=mid-1;i>left;i++){
        if(key==arr[i]) result.add(i);
        if(key<arr[i]) break;
    }
	return result;

5.斐波那契（黄金分割法）查找

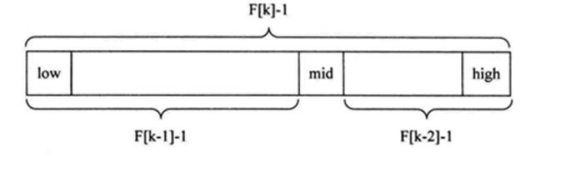
思路：斐波那契查找原理与前两种相似，仅仅改变了中间结点（mid）的位置，mid 不再是中间或插值得到，而是位于黄金分割点附近，即 mid=low+F(k-1)-1（F 代表斐波那契数列）

计算斐波那契数列

	public static int[] fib() {
		int[] f = new int[maxSize];
		f[0] = 1;
		f[1] = 1;
		for (int i = 2; i < maxSize; i++) {
			f[i] = f[i - 1] + f[i - 2];
		}
		return f;
	}

斐波那契数列查询的实现：

	public int fibSearch(arr[],int key){
        int low;		//左边界
        int high;		//右边界
        int mid;		//初始化分界点
        int k = 0; 		//表示斐波那契分割数值的下标
        int f[]=fib();		//斐波那契数列
        while(high > f[k] - 1) {		//获取斐波那契数列的下标
            k++;
        }

        int[] temp = Arrays.copyOf(a, f[k]);		//因为f[k]值可能大于a的长度，使用 a 数组最后的数填充 temp
                       //举例:temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234}
        while (low <= high) {
            mid = low + f[k - 1] - 1;
            if(key < temp[mid]) {		//对左侧继续使用斐波那契查找
                high = mid - 1;
                k--;
            } else if ( key > temp[mid]) {		//对右侧继续使用斐波那契查找
               	low = mid + 1;
                k -= 2;
           	} else { 
                if(mid <= high) {
                	return mid;
                } else {	//mid>high的情况是取到扩展之后的值了，所以返回high就可以
                	return high;
                }
            }
        }
        return -1;
    }

k–和k-=2

继续拆分为两部分查找，