数学建模笔记—— 回归分析
数学建模笔记—— 回归分析
- 回归分析
- 1. 回归分析的一般步骤
- 2. 一元线性回归分析
- 2.1 具体过程
- 2.1.1 确定回归方程中的解释变量和被解释变量
- 2.1.2 确定回归模型和建立回归方程
- 2.1.3 利用回归直线进行估计和预测
- 2.1.4 对回归方程进行各种检验(补充)
- 1. 回归直线的拟合优度
- 2. 显著性检验
- 2.2 典型例题
- 2.2.1 进行手算
- 2.2.2 使用matlab进行计算
- 3. 多元线性回归分析
- 3.1 算法介绍
- 3.1.1 多元线性回归模型
- 3.1.2 线性模型 ( Y , X β , σ 2 I n ) (Y,X\beta ,\sigma^{2}I_{n}) (Y,Xβ,σ2In)考虑的主要问题
- 3.1.3 多元线性回归模型的参数估计
- 3.1.4 多元线性回归模型和回归系数的检验
- 3.1.5 多元线性回归模型的预测
- 3.2 使用matlab实现
- 3.3 多元线性回归中的逐步回归
- 3.4 典型例题
- 4. 非线性回归分析
- 4.1 模型原理
- 4.2 配曲线求解
- 4.2.1 常见的六类曲线
- 4.2.2 例题求解
- 4.3 多项式回归求解
- 4.3.1 一元多项式回归
- 4.3.2 多元二项式回归
- 4.4 一般求解
回归分析
在统计学中,回归分析( regression analysis)指的是确定俩种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器) 之间的关系。这种技术通常用于预测分析以及发现变量之间的因果关系。例如,司机的鲁莽驾驶与道路交通事故数量之间的关系,最好的研究方法就是回归。
1. 回归分析的一般步骤
- 确定回归方程中的解释变量和被解释变量
- 确定回归模型和建立回归方程
- 对回归方程进行各种检验
- 利用回归方程进行预测
2. 一元线性回归分析
2.1 具体过程
2.1.1 确定回归方程中的解释变量和被解释变量
- 因变量:被预测或被解释的变量,用 y y y表示
- 自变量:预测或解释因变量的一个或者多个变量,用 x x x表示
- 对于只有线性关系的两个变量,可以用一个方程来表示它们之间的线性关系
- 描述因变量 y y y如何依赖于自变量 x x x和误差项 ϵ \epsilon ϵ的方程称为回归模型
2.1.2 确定回归模型和建立回归方程
对于只涉及一个自变量的一元线性回归模型可表示为
y
=
β
0
+
β
1
x
+
ϵ
y=\beta_0+\beta_1x+\epsilon
y=β0+β1x+ϵ
在这个模型里:
- y y y叫做因变量或被解释变量
- x x x叫做自变量或解释变量
- β 0 \beta_0 β0表示截距
- β 1 \beta_1 β1表示斜率
- ϵ \epsilon ϵ表示误差项,反映除 x x x和y之间的线性关系之外的随机因素对 y y y的影响,是不可避免的
回归方程:
- 描述因变量 y y y的期望值如何依赖于自变量 x x x的方程称为回归方程。根据对一元线性回归模型的假设,可以得到它的回归方程为:
E ( y ) = β 0 + β 1 x E(y)=\beta_0+\beta_1x E(y)=β0+β1x
-
如果回归方程中的参数已知,对于一个给定的 x x x值,利用回归方程就能计算出 y y y的期望值
-
用样本统计量代替回归方程中的未知参数,就得到估计的回归方程,简称回归直线
参数的最小二乘法估计:
对于回归直线,关键在于求解参数,常用高斯提出的最小二乘法,它是使因变量的观察值
y
y
y与估计值之间的离差平方和达到最小来求解的
Q
=
∑
(
y
−
y
^
)
2
=
∑
(
y
−
β
^
0
−
β
^
1
x
)
2
Q=\sum(y-\hat{y} )^2=\sum\bigl(y-\hat{\beta}_0-\hat{\beta}_1x\bigr)^2
Q=∑(y−y^)2=∑(y−β^0−β^1x)2
展开可得:
Q
=
∑
(
y
−
y
^
)
2
=
∑
y
2
+
n
β
^
0
2
+
β
^
1
2
Σ
x
2
+
2
β
^
0
β
^
1
Σ
x
−
2
β
^
0
Σ
y
−
2
β
^
1
Σ
x
y
Q=\sum(y-\hat{y})^{2}=\sum y^{2}+n\hat{\beta}_{0}^{2}+\hat{\beta}_{1}^{2}\Sigma x^{2}+2\hat{\beta}_{0} \hat{\beta}_{1}\Sigma x-2\hat{\beta}_{0} \Sigma y-2\hat{\beta}_{1}\Sigma xy
Q=∑(y−y^)2=∑y2+nβ^02+β^12Σx2+2β^0β^1Σx−2β^0Σy−2β^1Σxy
为了求该式子的极值,对
β
0
\beta_0
β0和
β
1
\beta1
β1求偏导得:
{
∑
y
=
n
β
^
0
+
β
^
1
Σ
x
∑
x
y
=
2
β
^
0
Σ
x
+
β
^
1
Σ
x
2
\begin{cases}\sum y=n\hat{\beta}_0+\hat{\beta}_1\Sigma x\\\sum xy=2\hat{\beta}_0\Sigma x+\hat{\beta}_1\Sigma x^2\end{cases}
{∑y=nβ^0+β^1Σx∑xy=2β^0Σx+β^1Σx2
求解:
{
β
^
1
=
n
∑
x
y
−
∑
x
∑
y
n
∑
x
2
−
(
∑
x
)
2
β
^
0
=
y
ˉ
−
β
^
1
x
ˉ
\begin{cases}\hat{\beta}_1=\frac{n\sum xy-\sum x\sum y}{n\sum x^2-(\sum x)^2}\\ \hat{\beta}_0=\bar{y}-\hat{\beta}_1\bar{x}\end{cases}
{β^1=n∑x2−(∑x)2n∑xy−∑x∑yβ^0=yˉ−β^1xˉ
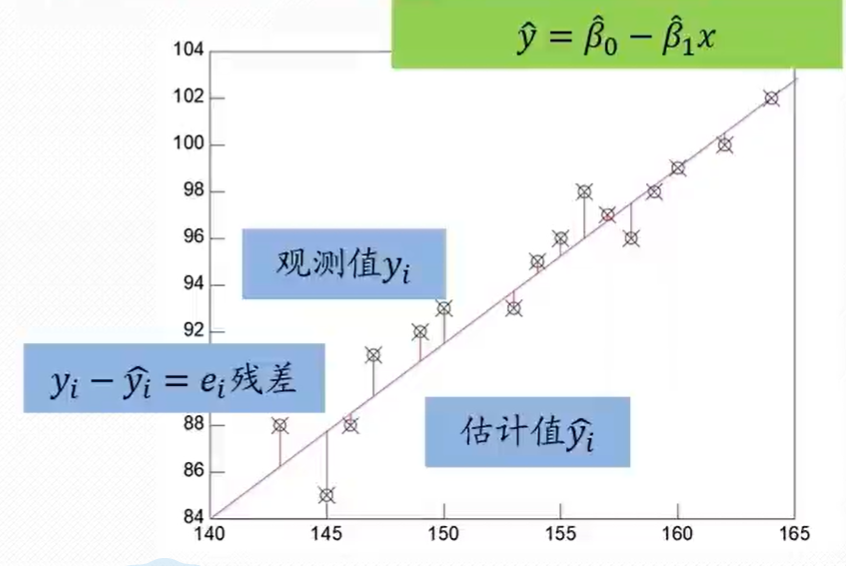
2.1.3 利用回归直线进行估计和预测
- 点估计:利用估计的回归方程,对于 x x x的某一个特定的值,求出 y y y的一个估计值就是点估计
- 区间估计:利用估计的回归方程,对于 x x x的一个特定值,求出 y y y的一个估计值的区间就是区间估计
估计标准误差的计算:
为了度量回归方程的可靠性,通常计算估计标准误差,它度量观察值回绕着回归直线的变化程度或分散程度,估计标准误差定义为:
S e = ∑ ( y − y ^ ) 2 n − 2 S_e=\sqrt{\frac{\sum(y-\hat{y})^2}{n-2}} Se=n−2∑(y−y^)2
- 估计标准误差越大,则数据点围绕回归直线的分散程度就越大,回归方程代表性就越小
- 估计标准误差越小,则数据点围绕回归直线的分散程度越小,回归方程的代表性越大,可靠性越高
置信区间和预测区间的估计:
置信区间:
y
^
0
±
t
α
2
S
e
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
−
x
ˉ
)
2
其中
α
为显著性水平,
t
α
可以通过查表得,
S
e
是估计标准误差
\hat{y}_0\pm t_{\frac\alpha2}S_e\sqrt{\frac1n+\frac{(x_0-\bar{x})^2}{\sum(x-\bar{x})^2}}\\ 其中\alpha 为显著性水平,t_\alpha可以通过查表得,S_e是估计标准误差
y^0±t2αSen1+∑(x−xˉ)2(x0−xˉ)2其中α为显著性水平,tα可以通过查表得,Se是估计标准误差
预测区间:
y
^
0
±
t
α
2
s
e
1
+
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
−
x
ˉ
)
2
其中
α
为显著性水平,
t
α
可以通过查表得,
S
e
是估计标准误差
\hat{y}_{0}\pm t_{\frac{\alpha}{2}}s_{e}\sqrt{1+\frac{1}{n}+\frac{(x_{0}-\bar{x})^{2}}{\sum(x-\bar{x})^{2}}}\\ 其中\alpha 为显著性水平,t_\alpha可以通过查表得,S_e是估计标准误差
y^0±t2αse1+n1+∑(x−xˉ)2(x0−xˉ)2其中α为显著性水平,tα可以通过查表得,Se是估计标准误差
2.1.4 对回归方程进行各种检验(补充)
1. 回归直线的拟合优度
回归直线与各观测点的接近程度称为回归直线对数据的拟合优度
-
总平方和 (TSS):反映因变量的 n n n个观察值与其均值的总离差
T S S = ∑ y i 2 = ∑ ( y i − y ˉ i ) 2 TSS=\sum y_i^2=\sum(y_i-\bar{y}_i)^2 TSS=∑yi2=∑(yi−yˉi)2 -
回归平方和 (ESS):反映了 y y y的总变差中,由于 x x x与 y y y之间的线性关系引起的 y y y的变化部分
E S S = ∑ y ^ i 2 = ∑ ( y ^ i − y ˉ i ) 2 ESS=\sum\hat{y}_i^2=\sum(\hat{y}_i-\bar{y}_i)^2 ESS=∑y^i2=∑(y^i−yˉi)2 -
残差平方和(RSS):反映了除了 x x x对 y y y的线性影响之外的其他因素对 y y y变差的作用,是不能由回归直线来解释的y的变差部分
R S S = ∑ e i 2 = ∑ ( y i − y ^ i ) 2 RSS=\sum e_{i}^{2}=\sum(y_{i}-\hat{y}_{i})^{2} RSS=∑ei2=∑(yi−y^i)2
总平方和可以分解为回归平方和、残差平方和两部分:
T
S
S
=
E
S
S
+
R
S
S
TSS=ESS+RSS
TSS=ESS+RSS
判定系数:
回归平方和占总平方和的比例,用
R
R
R表示,其值在0到1之间
R
2
=
E
S
S
T
S
S
=
1
−
R
S
S
T
S
S
=
∑
(
y
^
i
−
y
ˉ
i
)
2
∑
(
y
i
−
y
ˉ
i
)
2
R^{2}=\frac{\mathrm{ESS}}{T\mathrm{SS}}=1-\frac{\mathrm{RSS}}{T\mathrm{SS}}=\frac{\sum(\hat{y}_{i}-\bar{y}_{i})^{2}}{\sum(y_{i}-\bar{y}_{i})^{2}}
R2=TSSESS=1−TSSRSS=∑(yi−yˉi)2∑(y^i−yˉi)2
- R 2 = 0 R^2=0 R2=0:说明 y y y的变化与 x x x无关, x x x无助于解释 y y y的变差
- R 2 = 1 R^2=1 R2=1:说明残差平方和为0,拟合是完全的, y y y的变化只与 x x x有关
2. 显著性检验
显著性检验的主要目的是根据所建立的估计方程用自变量 x x x来估计或预测因变量 y y y的取值,当建立了估计方程后,还不能马上进行估计或预测,因为该估计方程是根据样本数据得到的,它是否真实的反映了变量 x x x和 y y y之间的关系,则需要通过检验后才能证实。
根据样本数据拟合回归方程时,实际上就已经假定变量 x x x和 y y y之间存在着线性关系,并假定误差项是一个服从正态分布的随机变量,且具有相同的方差,但这些假设是否成立需要检验。
显著性检验包括两方面:
-
线性关系检验
线性关系检验是检验自变量 x x x和因变量y之间的线性关系是否显著,或者说,它们之间能否用一个线性模型来表示
检验原理:
将均方回归(MSR)同均方残差(MSE)加以比较,应用F检验来分析二者之间的差别是否显著
- 均方回归(MSR):回归平方和ESS除以相应的回归自由度(自变量的个数k)
- 均方残差(MSE):残差平方和RSS除以相应的残差自由度(n-k+1)
检验过程:
-
H 0 H_0 H0(原假设): β 1 = 0 \beta_1=0 β1=0,回归系数与0无显著差异, y y y与 x x x的线性关系不显著
-
H 1 H_1 H1: β 1 ≠ 0 \beta_1\neq0 β1=0, 回归显著,认为 y y y与 x x x存在线性关系,所求的线性回归方程有意义
-
计算检验统计量 F : F: F:
H 0 H_0 H0成立时
F = E S S / 1 R S S / ( n − 2 ) = M S R M S E ∼ F ( 1 , n − 2 ) F=\frac{ESS/1}{RSS/(n-2)}=\frac{MSR}{MSE}\sim F(1,n-2) F=RSS/(n−2)ESS/1=MSEMSR∼F(1,n−2)
若 F > F 1 − α ( 1 , n − 2 ) F> F_{1-\alpha}(1,n-2) F>F1−α(1,n−2),拒绝 H 0 H_0 H0,否则接受 H 0 H_0 H0
-
回归系数检验
回归系数显著性检验的目的是通过检验回归系数 β \beta β的值与0是否有显著性差异,来判断 Y Y Y与 X X X之间是否有显著的线性关系,若 β = 0 \beta=0 β=0,则总体回归方程中不含 X X X项(即 Y Y Y不随 X X X变动而变动),因此,变量 Y Y Y与 X X X之间并不存在线性关系;若 β ≠ 0 \beta\neq0 β=0, 说明变量 Y Y Y与 X X X之间存在显著的线性关系。
β ^ 1 \hat{\beta } _1 β^1是根据最小二乘法求出的样本统计量,服从正态分布
β ^ 1 \hat{\beta } _1 β^1的分布具有如下性质:
-
数学期望: E ( β ^ 1 ) = β 1 E(\hat{\beta}_1)=\beta_1 E(β^1)=β1
-
标准差: σ β ^ 1 = σ ∑ x i 2 − 1 n ( ∑ x i ) 2 \sigma_{\widehat{\beta}_1}=\frac\sigma{\sqrt{\sum x_i^2-\frac1n(\sum x_i)^2}} σβ 1=∑xi2−n1(∑xi)2σ
由于 σ \sigma σ未知,需用其估计量 S e S_\mathrm{e} Se来代替得到 β ^ 1 \hat{\beta}_1 β^1的估计标准差
S β ^ 1 = S e ∑ x i 2 − 1 n ( ∑ x i ) 2 S e = ∑ ( y i − y ^ i ) 2 n − k − 1 = M S E S_{\widehat{\beta}_{1}}=\frac{S_{e}}{\sqrt{\sum x_{i}^{2}-\frac{1}{n}(\sum x_{i})^{2}}}\quad S_{e}=\sqrt{\frac{\sum(y_{i}-\hat{y}_{i})^{2}}{n-k-1}}=\sqrt{MSE} Sβ 1=∑xi2−n1(∑xi)2SeSe=n−k−1∑(yi−y^i)2=MSE
t t t检验的统计量:
t = β ^ 1 − β 1 s β ^ 1 ∼ t ( n − 2 ) t=\frac{\widehat{\beta}_1-\beta_1}{s_{\widehat{\beta}_1}}\sim t(n-2) t=sβ 1β 1−β1∼t(n−2) -
线性关系检验与回归系数检验的区别:
线性关系的检验是检验自变量与因变量是否可以用线性来表达,而回归系数的检验是对样本数据计算的回归系数检验是否为0
- 在一元线性回归中,自变量只有一个,线性关系检验与回归系数检验是等价的
- 在多元回归分析中,这两种检验的意义是不同的。线性关系检验只能用来检验总体回归关系的显著性,而回归系数检验可以对各个回归系数分别进行检验
2.2 典型例题
某团队测了16名成年女子的身高与腿长所得数据如下
身高 143 145 146 147 49 153 154 155 156 157 158 159 160 162 164 腿长 88 85 88 91 92 93 95 96 98 97 96 98 999 100 102 我们发现,腿长和身高有很强的正相关性,身高越高,腿长越长,那么通过这组数据,我们可以预测身高170的成年女性腿长是多长吗?
2.2.1 进行手算
一元线性表达式为:
y
^
=
β
^
0
+
β
^
1
x
\widehat{y}=\widehat{\beta}_{0}+\widehat{\beta}_{1}x
y
=β
0+β
1x
对参数进行最小二乘估计:
{
β
^
1
=
n
∑
x
y
−
∑
x
∑
y
n
∑
x
2
−
(
∑
x
)
2
=
16
×
232566
−
2458
×
1511
16
×
378220
−
245
8
2
=
0.7194
β
^
0
=
y
ˉ
−
β
^
1
x
ˉ
=
94.4375
−
0.7194
×
153.625
=
−
16.08
\begin{cases}\hat{\beta}_{1}=\frac{n\sum xy-\sum x\sum y}{n\sum x^{2}-(\sum x)^{2}}=\frac{16\times232566-2458\times1511}{16\times378220-2458^{2}}=0.7194\\ \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1}\bar{x}=94.4375-0.7194\times153.625=-16.08\end{cases}
{β^1=n∑x2−(∑x)2n∑xy−∑x∑y=16×378220−2458216×232566−2458×1511=0.7194β^0=yˉ−β^1xˉ=94.4375−0.7194×153.625=−16.08
将估计得到的参数代回一元线性表达式:
y
^
=
0.794
x
−
16.08
\widehat{y}=0.794x-16.08
y
=0.794x−16.08
进行预测:
x
=
170
,
y
^
=
106.218
x=170,\widehat{y}=106.218
x=170,y
=106.218
预测身高170的成年女性腿长是106.218cm
计算估计标准误差:
s
e
=
∑
(
y
−
y
^
)
2
n
−
2
=
1.744
=
1.32
s_{e}=\sqrt{\frac{\sum(y-\hat{y})^{2}}{n-2}}=\sqrt{1.744}=1.32
se=n−2∑(y−y^)2=1.744=1.32
我们令显著性水平
α
=
0.05
\alpha=0.05
α=0.05,则置信水平
1
−
α
=
0.95
1-\alpha=0.95
1−α=0.95
自由度为16,计算
t
α
t
t_{\frac{\alpha}{t}}
ttα
t
α
2
(
n
−
k
)
=
t
0.025
(
16
−
2
)
=
t
0.025
(
14
)
=
2.145
(
查表
)
t_{\frac{\alpha}{2}}(n-k)=t_{0.025}(16-2)=t_{0.025}(14)=2.145(\text{查表})
t2α(n−k)=t0.025(16−2)=t0.025(14)=2.145(查表)
置信区间为:
y
^
0
±
t
α
2
s
e
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
−
x
ˉ
)
2
=
106.218
±
2.007
\hat{y}_{0}\pm t_{\frac{\alpha}{2}}s_{e}\sqrt{\frac{1}{n}+\frac{(x_{0}-\bar{x})^{2}}{\sum(x-\bar{x})^{2}}}=106.218\pm2.007
y^0±t2αsen1+∑(x−xˉ)2(x0−xˉ)2=106.218±2.007
预测区间为:
y
^
0
±
t
α
2
s
e
1
+
1
n
+
(
x
0
−
x
ˉ
)
2
∑
(
x
−
x
ˉ
)
2
=
106.218
±
3.472
\widehat{y}_{0}\pm t_{\frac{\alpha}{2}}s_{e}\sqrt{1+\frac{1}{n}+\frac{(x_{0}-\bar{x})^{2}}{\sum(x-\bar{x})^{2}}}=106.218\pm3.472
y
0±t2αse1+n1+∑(x−xˉ)2(x0−xˉ)2=106.218±3.472
判定系数为:
R
2
=
E
S
S
T
S
S
=
1
−
R
S
S
T
S
S
=
∑
‾
(
y
^
i
−
y
ˉ
i
)
2
∑
(
y
i
−
y
ˉ
i
)
2
=
1
−
∑
(
y
i
−
y
^
i
)
2
∑
(
y
i
−
y
ˉ
i
)
2
=
0.9282
,
是比较接近与1的
R^{2}=\frac{\mathrm{ESS}}{T\mathrm{SS}}=1-\frac{\mathrm{RSS}}{T\mathrm{SS}}=\frac{\overline{\sum}(\hat{y}_{i}-\bar{y}_{i})^{2}}{\sum(y_{i}-\bar{y}_{i})^{2}}=1-\frac{\sum(y_{i}-\hat{y}_{i})^{2}}{\sum(y_{i}-\bar{y}_{i})^{2}}=0.9282,\text{ 是比较接近与1的}
R2=TSSESS=1−TSSRSS=∑(yi−yˉi)2∑(y^i−yˉi)2=1−∑(yi−yˉi)2∑(yi−y^i)2=0.9282, 是比较接近与1的
进行线性关系检验:
F
=
E
S
S
/
1
R
S
S
/
(
n
−
2
)
=
M
S
R
M
S
E
∼
F
(
1
,
n
−
2
)
=
180.9631
>
4.6
F=\frac{ESS/1}{RSS/(n-2)}=\frac{MSR}{MSE}\sim F(1,n-2)=180.9631>4.6
F=RSS/(n−2)ESS/1=MSEMSR∼F(1,n−2)=180.9631>4.6
所以线性关系显著
2.2.2 使用matlab进行计算
[ b , b i n t , r , r i n t , s t a t s ] = r e g r e s s ( Y , X , a l p h a ) [b,bint,r,rint,stats]=regress(Y,X,alpha) [b,bint,r,rint,stats]=regress(Y,X,alpha)
-
输入变量
- X , Y X,Y X,Y——自变量和因变量的样本值
- a l p h a alpha alpha——显著性水平,默认为0.05
-
输出变量
-
b b b——回归系数
-
b i n t bint bint——回归系数的区间估计
-
r r r——残差
-
r i n t rint rint——置信区间
-
s t a t s stats stats——用于检验回归模型的统计量
s t a t s stats stats有四个数值:决定系数 R 2 R^2 R2、 F F F值、与 F F F对应的概率 P P P、无偏估计 σ \sigma σ
-
具体代码:
% 1. 输入数据
% 输入X的样本值
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
% 插入\beta_0对应列
X=[ones(16,1) x];
% 输入Y的样本值
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
% 2. 回归分析及检验
[b,bint,r,rint,stats]=regress(Y,X);
b,bint,stats
% 3. 残差分析,作残差图
rcoplot(r,rint)
% 4. 预测及作图
z=b(1)+b(2)*x;
plot(x,Y,'k+',x,z,'r')
输出:
b =
-16.0730
0.7194
bint =
-33.7071 1.5612
0.6047 0.8340
stats =
0.9282 180.9531 0.0000 1.7437
得到的残差图:
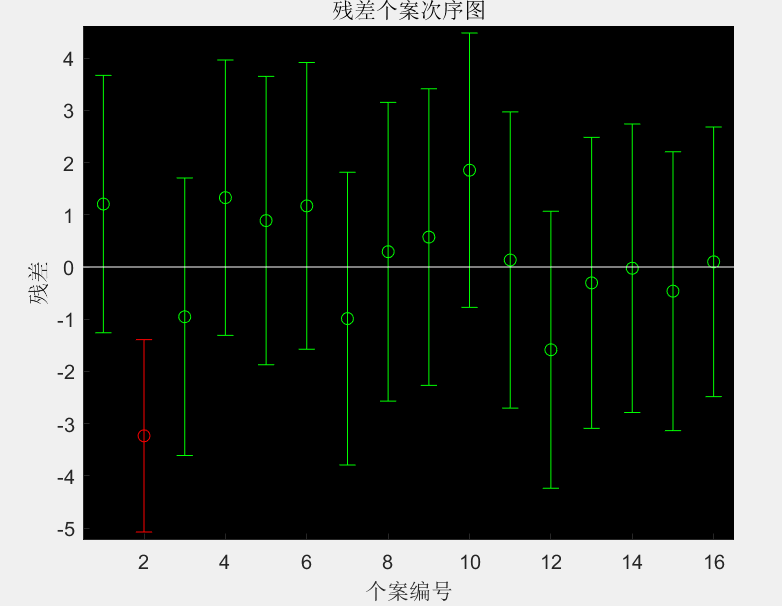
得到的回归曲线:
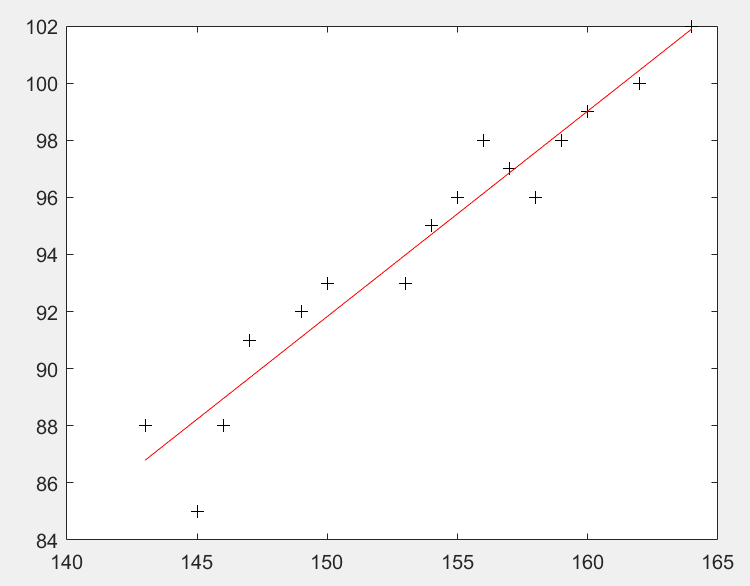
3. 多元线性回归分析
经常会遇到某一现象的发展和变化取决于(几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况,这时需用多元线性回归分析,多元线性回归分析预测法,是指通过对两个或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测和控制的方法
3.1 算法介绍
3.1.1 多元线性回归模型
一般称由
y
=
β
0
+
β
1
x
1
+
⋯
+
β
k
x
k
y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{k}x_{k}
y=β0+β1x1+⋯+βkxk确定的模型:
{
Y
=
X
β
+
ϵ
E
(
ϵ
)
=
0
,
C
O
V
(
ϵ
,
ϵ
)
=
σ
2
I
n
\left\{\begin{matrix}Y=X\beta+\epsilon\\ E(\epsilon)=0 ,COV(\epsilon ,\epsilon)=\sigma^2I_n\end{matrix}\right.
{Y=Xβ+ϵE(ϵ)=0,COV(ϵ,ϵ)=σ2In
为
k
k
k元线性回归模型,并简记为
(
Y
,
X
β
,
σ
2
I
n
)
(Y,X\beta ,\sigma^{2}I_{n})
(Y,Xβ,σ2In)
其中
Y
=
[
y
1
y
2
.
.
.
y
n
]
,
X
=
[
1
x
11
x
12
⋯
x
1
k
1
x
21
x
22
⋯
x
2
k
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
x
n
1
x
n
2
⋯
x
n
k
]
,
β
=
[
β
0
β
1
.
.
.
β
k
]
,
ϵ
=
[
ϵ
1
ϵ
2
.
.
.
ϵ
n
]
Y=\begin{bmatrix}y_{1}\\y_{2}\\...\\y_{n}\end{bmatrix} ,X=\begin{bmatrix}1&x_{11}&x_{12}&\cdots&x_{1k}\\1&x_{21}&x_{22}&\cdots&x_{2k}\\...&...&...&...&...\\1&x_{n1}&x_{n2}&\cdots&x_{nk}\end{bmatrix} ,\beta=\begin{bmatrix}\beta_{0}\\\beta_{1}\\...\\\beta_{k}\end{bmatrix} ,\epsilon=\begin{bmatrix}\epsilon_{1}\\\epsilon_{2}\\...\\\epsilon_{n}\end{bmatrix}
Y=
y1y2...yn
,X=
11...1x11x21...xn1x12x22...xn2⋯⋯...⋯x1kx2k...xnk
,β=
β0β1...βk
,ϵ=
ϵ1ϵ2...ϵn
y
=
β
0
+
β
1
x
1
+
⋯
+
β
k
x
k
y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{k}x_{k}
y=β0+β1x1+⋯+βkxk称为回归平面方程
3.1.2 线性模型 ( Y , X β , σ 2 I n ) (Y,X\beta ,\sigma^{2}I_{n}) (Y,Xβ,σ2In)考虑的主要问题
- 对参数β和 σ 2 σ^2 σ2作点估计,建立 y y y与 x 1 , x 2 , ⋅ ⋅ ⋅ , x k x_1,x_2,\cdotp\cdotp\cdotp,x_k x1,x2,⋅⋅⋅,xk之间的数量关系
- 对模型参数、模型结果等做检验
- 对 γ \gamma γ的值作预测,即对 γ \gamma γ作点(区间)估计
3.1.3 多元线性回归模型的参数估计
用最小二乘法求
β
0
,
.
.
.
,
β
k
\beta_0,...,\beta_k
β0,...,βk的估计量:作离差平方和
Q
=
∑
i
=
1
n
(
y
i
−
β
0
−
β
1
x
i
1
−
⋯
−
β
k
x
i
k
)
2
Q=\sum_{i=1}^{n}(y_{i}-\beta_{0}-\beta_{1}x_{i1}-\cdots-\beta_{k}x_{ik})^{2}
Q=i=1∑n(yi−β0−β1xi1−⋯−βkxik)2
选择
β
0
,
.
.
.
,
β
k
\beta_0,...,\beta_k
β0,...,βk使
Q
Q
Q达到最小,解得估计值:
β
^
=
(
X
T
X
)
−
1
(
X
T
Y
)
\hat{\beta}=(X^{T}X)^{-1}(X^{T}Y)
β^=(XTX)−1(XTY)
将得到的
β
i
^
\hat{\beta_i}
βi^代入回归平面方程得:
y
=
β
^
0
+
β
^
1
x
1
+
⋯
+
β
^
k
x
k
y=\hat{\beta}_0+\hat{\beta}_1x_1+\cdots+\hat{\beta}_kx_k
y=β^0+β^1x1+⋯+β^kxk
称为经验回归平面方程,
β
i
^
\hat{\beta_i}
βi^称为经验回归系数
3.1.4 多元线性回归模型和回归系数的检验
-
F F F检验法
当 H 0 H_0 H0成立时
F = U / k Q e / ( n − k − 1 ) ∼ F ( k , n − k − 1 ) 其中 U = ∑ i = 1 n ( y ^ i − y ˉ ) 2 ( 回归平方和 ) , Q e = ∑ i = 1 n ( y i − y ^ i ) 2 ( 残差平方和 ) F=\frac{U/k}{Q_{e}/(n-k-1)}\sim F(k,n-k-1)\\ 其中U=\sum_{i=1}^n(\hat{y}_i-\bar{y})^2\left(\text{回归平方和}\right),\quad Q_e=\sum_{i=1}^n(y_i-\hat{y}_i)^2(残差平方和) F=Qe/(n−k−1)U/k∼F(k,n−k−1)其中U=i=1∑n(y^i−yˉ)2(回归平方和),Qe=i=1∑n(yi−y^i)2(残差平方和)
如果 F > F 1 − α ( k , n − k − 1 ) F>F_{1-\alpha}(k,n-k-1) F>F1−α(k,n−k−1),则拒绝 H 0 H_0 H0,认为 y y y与 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk之间显著地有线性关系;否则就接受 H 0 H_0 H0,认为 y y y与 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk之间线性关系不显著。 -
r r r检验法
定义:
R = U L y y = U U + Q e R=\sqrt{\frac{U}{L_{yy}}}=\sqrt{\frac{U}{U+Q_{e}}} R=LyyU=U+QeU
称 y y y与 x 1 , . . . , x k x_1,...,x_k x1,...,xk的多元相关系数或复相关系数,由于
F = n − k − 1 k R 2 1 − R 2 F=\frac{n-k-1}k\frac{R^2}{1-R^2} F=kn−k−11−R2R2
故 F F F与 R R R的检验是等效的
3.1.5 多元线性回归模型的预测
-
点预测
求出回归方程 y ^ = β ^ 0 + β ^ 1 x 1 + ⋯ + β ^ k x k \hat{y}=\hat{\beta}_0+\hat{\beta}_1x_1+\cdots+\hat{\beta}_kx_k y^=β^0+β^1x1+⋯+β^kxk, 对于给定自变量的值 x 1 ∗ , ⋯ , x k ∗ x_1^*,\cdots,x_k^* x1∗,⋯,xk∗, 用 y ^ ∗ = β ^ 0 + β ^ 1 x 1 ∗ + ⋯ + \hat{y}^*=\hat{\beta}_0+\hat{\beta}_1x_1^*+\cdots+ y^∗=β^0+β^1x1∗+⋯+
β ^ k x k ∗ \hat{\beta}_kx_k^* β^kxk∗来预测 y ∗ = β 0 + β 1 x 1 ∗ + ⋯ + β k x k ∗ + ϵ y^*=\beta_0+\beta_1x_1^*+\cdots+\beta_kx_k^*+\epsilon y∗=β0+β1x1∗+⋯+βkxk∗+ϵ,称 γ ^ ∗ \hat{\gamma}^* γ^∗为 y ∗ y^* y∗的点预测 -
区间预测
y y y的 1 − α 1-\alpha 1−α的预测区间(置信)区间为( y ^ 1 , y ^ 2 ) \hat{y}_1,\hat{y}_2) y^1,y^2), 其中
{ y ^ 1 = y ^ − σ ^ e 1 + ∑ i = 0 k ∑ j = 0 k c i j x i x j t 1 − α 2 ( n − k − 1 ) y ^ 2 = y ^ + σ ^ e 1 + ∑ i = 0 k ∑ j = 0 k c i j x i x j t 1 − α 2 ( n − k − 1 ) \begin{cases}\hat{y}_{1}=\hat{y}-\hat{\sigma}_{e}\sqrt{1+\sum_{i=0}^{k}\sum_{j=0}^{k}c_{ij}x_{i}x_{j}t_{1-\frac{\alpha}{2}}(n-k-1)}\\\hat{y}_{2}=\hat{y}+\hat{\sigma}_{e}\sqrt{1+\sum_{i=0}^{k}\sum_{j=0}^{k}c_{ij}x_{i}x_{j}t_{1-\frac{\alpha}{2}}(n-k-1)}\\\end{cases}\\ ⎩ ⎨ ⎧y^1=y^−σ^e1+∑i=0k∑j=0kcijxixjt1−2α(n−k−1)y^2=y^+σ^e1+∑i=0k∑j=0kcijxixjt1−2α(n−k−1)C = L − 1 = ( c i j ) , L = X ′ X C=L^{-1}=\left(c_{ij}\right),L=X^{\prime}X C=L−1=(cij),L=X′X
3.2 使用matlab实现
[ b , b i n t , r , r i n t , s t a t s ] = r e g r e s s ( Y , X , a l p h a ) [b,bint,r,rint,stats]=regress(Y,X,alpha) [b,bint,r,rint,stats]=regress(Y,X,alpha)
-
输入变量
- X , Y X,Y X,Y——自变量和因变量的样本值
- a l p h a alpha alpha——显著性水平,默认为0.05
-
输出变量
-
b b b——回归系数
-
b i n t bint bint——回归系数的区间估计
-
r r r——残差
-
r i n t rint rint——置信区间
-
s t a t s stats stats——用于检验回归模型的统计量
s t a t s stats stats有四个数值:决定系数 R 2 R^2 R2、 F F F值、与 F F F对应的概率 P P P、无偏估计 σ \sigma σ
-
b = [ β ^ 0 β ^ 1 . . . β ^ p ] , Y = [ y 1 y 2 . . . y n ] , X = [ 1 x 11 x 12 ⋯ x 1 p 1 x 21 x 22 ⋯ x 2 p . . . . . . . . . . . . . . . 1 x n 1 x n 2 ⋯ x n p ] b=\begin{bmatrix}\hat{\beta}_0\\\hat{\beta}_1\\...\\\hat{\beta}_p\end{bmatrix},Y=\begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix} ,X=\begin{bmatrix}1&x_{11}&x_{12}&\cdots&x_{1p}\\1&x_{21}&x_{22}&\cdots&x_{2p}\\...&...&...&...&...\\1&x_{n1}&x_{n2}&\cdots&x_{np}\end{bmatrix} b= β^0β^1...β^p ,Y= y1y2...yn ,X= 11...1x11x21...xn1x12x22...xn2⋯⋯...⋯x1px2p...xnp
3.3 多元线性回归中的逐步回归
“最优”的回归方程就是包含所有对
Y
Y
Y有影响的变量,而不包含对Y影响不显者的变量回归方程
逐步回归分析法的思想:
- 从一个自变量开始,根据自变量对 Y Y Y作用的显著程度,从大到小地依次逐个引入回归方程。
- 当引入的自变量由于后引入变量而变得不显著时,要将其剔除掉。
- 引入一个自变量或从回归方程中剔除一个自变量,为逐步回归的一步。
- 对于每一步都要进行 Y Y Y值检验,以确保每次引入新的显著性变量前回归方程中只包含对 Y Y Y作用显著的变量。
- 这个过程反复进行,直至既无不显著的变量从回归方程中剔除,又无显著变量可引入回归方程时为止。
逐步回归的matlab实现:
s t e p w i s e ( x , y , i n m o d e l , a l p h a ) stepwise(x,y,inmodel,alpha) stepwise(x,y,inmodel,alpha)
- x x x——自变量数据, n × m n\times m n×m阶矩阵
- y y y——因变量数据, n × 1 n\times 1 n×1阶矩阵
- i n m o d e l inmodel inmodel——矩阵的列数的指标,给出初始模型中包含的子集(缺省时设定为全部自变量)
- a l p h a alpha alpha——默认为0.05
3.4 典型例题
例1:
某建材公司对某年20个地区的建材销售量 Y Y Y(千方)、推销开支、实际帐目数、同类商品竞争数和地区销售潜力分别进行了统计。试分析推销开支、实际帐目数、同类商品竞争数和地区销售潜力对建材销售量的影响作用。试建立回归模型,且分析哪些是主要的影响因素。
序号 推销开支 实际账目数 同类商品竞争数 地区销售潜力 建材销售量 1 5.5 31 10 8 79.3 2 2.5 55 8 6 200.1 3 8.0 67 12 9 163.2 4 3.0 50 7 16 200.1 5 3.0 38 8 15 146.0 6 2.9 71 12 17 177.7 7 8.0 30 12 8 30.9 8 9.0 56 5 10 291.9 9 4.0 42 8 4 160.0 10 6.5 73 5 16 339.4 11 5.5 60 11 7 159.6 12 5.0 44 12 12 86.3 13 6.0 50 6 6 237.5 14 5.0 39 10 4 107.2 15 3.5 55 10 4 155.0 16 8.0 70 6 14 201.4 17 6.0 40 11 6 100.2 18 4.0 50 11 8 135.8 19 7.5 62 9 13 223.3 20 7.0 59 9 11 195.0
设:
- 推销开支 − − x 1 --x_1 −−x1
- 实际账目数—— x 2 x_2 x2
- 同类商品竞争数—— x 3 x_3 x3
- 地区销售潜力一一 x 4 x_4 x4
clc
clear
% 1. 数据输入
x1 = [5.5, 2.5, 8.0, 3.0, 3.0, 2.9, 8.0, 9.0, 4.0, 6.5, 5.5, 5.0, 6.0, 5.0, 3.5, 8.0, 6.0, 4.0, 7.5, 7.0]';
x2 = [31, 55, 67, 50, 38, 71, 30, 56, 42, 73, 60, 44, 50, 39, 55, 70, 40, 50, 62, 59]';
x3 = [10, 8, 12, 7, 8, 12, 12, 5, 8, 5, 11, 12, 6, 10, 10, 6, 11, 11, 9, 9]';
x4 = [8, 6, 9, 16, 15, 17, 8, 10, 4, 16, 7, 12, 6, 4, 4, 14, 6, 8, 13, 11]';
y = [79.3, 200.1, 163.2, 200.1, 146.0, 177.7, 30.9, 291.9, 160.0, 339.4, 159.6, 86.3, 237.5, 107.2, 155.0, 201.4, 100.2, 135.8, 223.3, 195.0]';
X=[ones(size(x1)),x1,x2,x3,x4];
% 2. 求结果
[b,bint,r,rint,stats]=regress(y,X)
% 3. 画残差图
rcoplot(r,rint)
输出:
b =
191.9158
-0.7719
3.1725
-19.6811
-0.4501
bint =
103.1071 280.7245
-7.1445 5.6007
2.0640 4.2809
-25.1651 -14.1972
-3.7284 2.8283
r =
-6.3045
-4.2215
5.1293
-3.1536
0.0469
6.6035
-10.2401
32.1803
-2.8219
26.5194
1.2254
0.2303
12.3801
-5.9704
-10.0875
-82.0245
5.2103
8.4422
23.4625
3.3938
rint =
-56.5085 43.8995
-51.7960 43.3530
-40.4734 50.7319
-49.7055 43.3983
-44.3616 44.4554
-33.2319 46.4388
-53.1505 32.6704
-9.9247 74.2853
-52.7697 47.1259
-17.9495 70.9883
-50.3051 52.7559
-50.3940 50.8545
-37.1038 61.8641
-57.7043 45.7635
-58.2382 38.0632
-94.9983 -69.0506
-47.1746 57.5953
-44.4834 61.3677
-26.9939 73.9190
-50.3179 57.1054
stats =
0.9034 35.0509 0.0000 644.6510
得到的残差图:
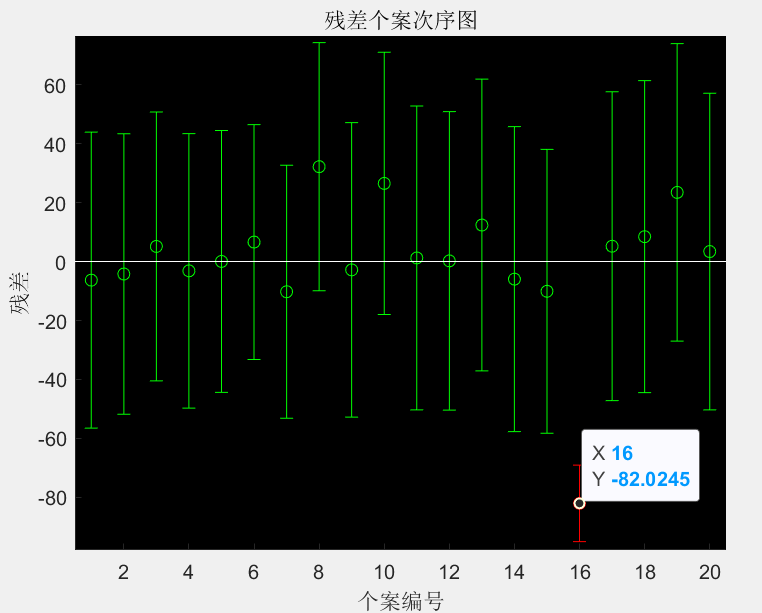
例2:
水泥凝固时放出的热量y与水泥中4种化学成分 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4有关,今测得一组数据如下,试用逐步回归法确定一个线性模型
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 x 1 x_1 x1 7 1 11 11 7 11 3 1 2 21 1 11 10 x 2 x_2 x2 26 29 56 31 52 55 71 31 54 47 40 66 68 x 3 x_3 x3 6 15 8 8 6 9 17 22 18 4 23 9 8 x 4 x_4 x4 60 52 20 47 33 22 6 44 22 26 34 12 12 y y y 78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4
使用逐步回归法确定模型
clc
clear
% 1. 数据输入
x1 = [7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10]';
x2 = [26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68]';
x3 = [6, 15, 8, 8, 6, 9, 17, 22, 18, 4, 23, 9, 8]';
x4 = [60, 52, 20, 47, 33, 22, 6, 44, 22, 26, 34, 12, 12]';
y = [78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, 93.1, 115.9, 83.8, 113.3, 109.4]';
x=[x1 x2 x3 x4];
% 2. 逐步回归
stepwise(x,y)
-
先在初始模型中取全部自变量
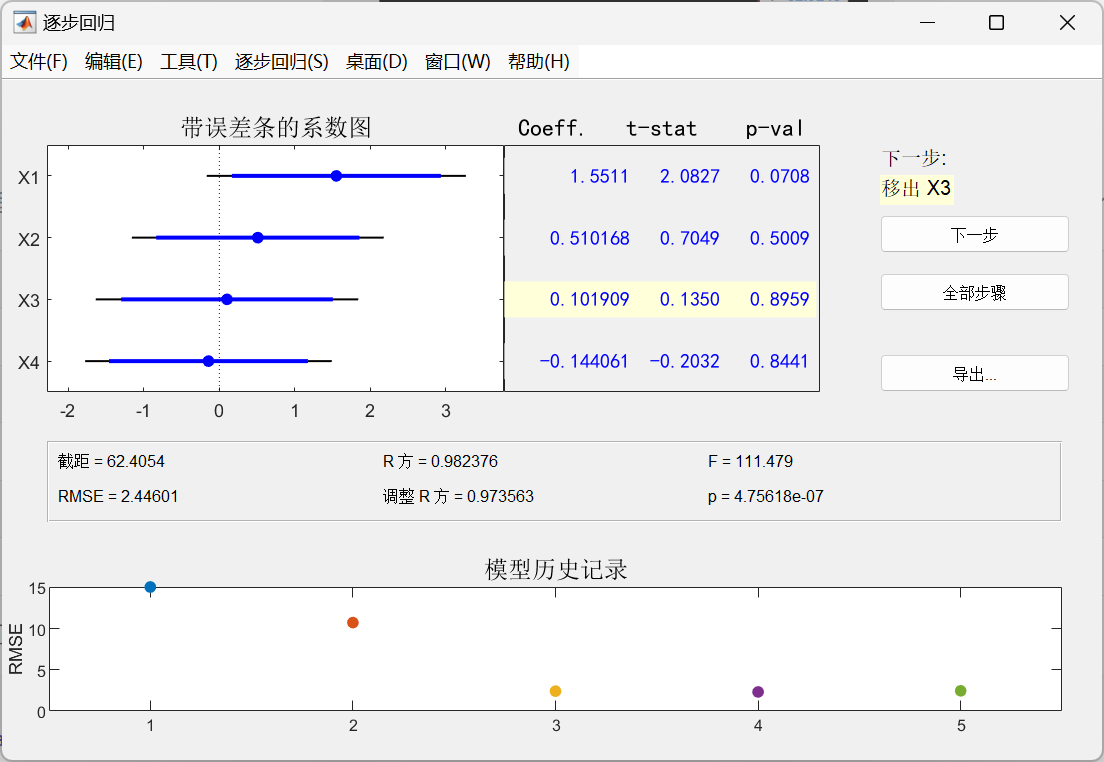
-
点击直线3和直线4来移除变量 x 3 x_3 x3和变量 x 4 x_4 x4
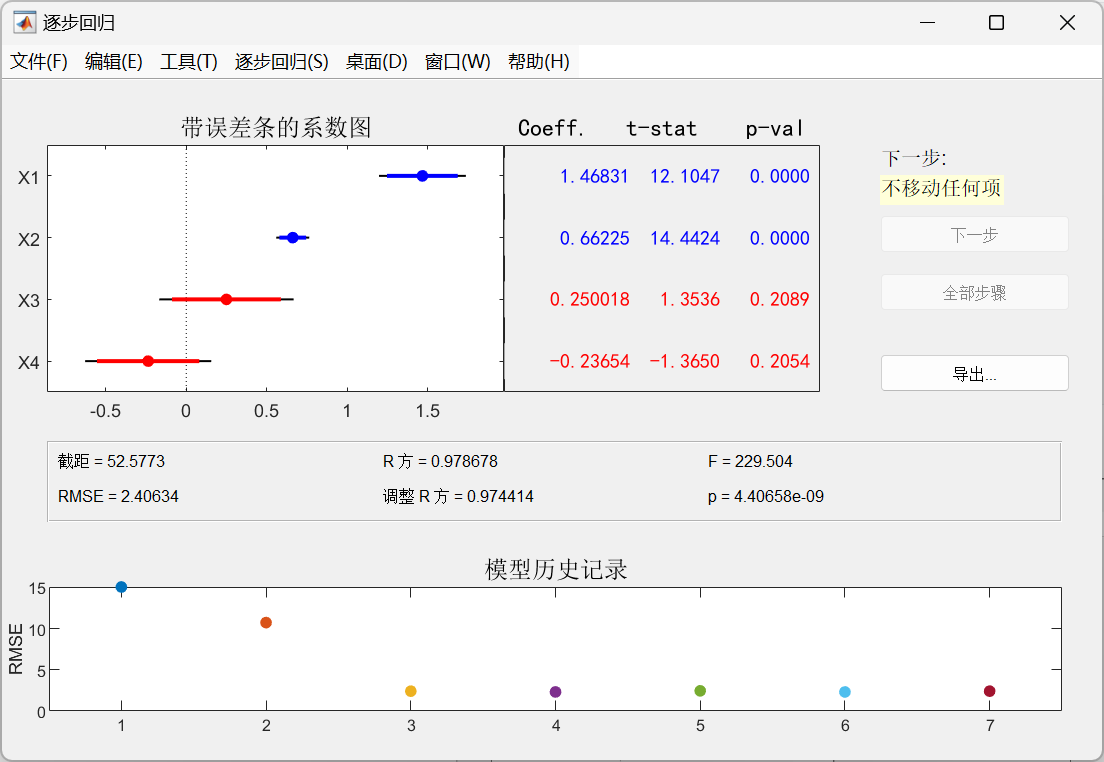
进行线性回归
% 3. 线性回归
X=[ones(13,1) x1 x2];
b=regress(y,X)
输出:
b =
52.5773
1.4683
0.6623
绘图:
% 4. 作图
% 定义自变量的范围
x1=-10:0.1:10;
x2=-10:0.1:10;
% 计算对应的因变量值
[X1,X2]=meshgrid(x1,x2); % 创建网格点坐标矩阵
Z=52.5773+1.4683*X1+0.6623*X2;
% 绘制三维图形
figure
surf(X1,X2,Z);
xlabel('x1')
ylabel('x2')
zlabel('z')
title('Z=52.5773+1.4683*X1+0.6623*X2')
输出:

4. 非线性回归分析
4.1 模型原理
直线关系是两变量向最简单的一种关系,曲线回归分析的基本任务是通过两个相关变量 x x x与 y y y的实际观测数据建立曲线回归方程,以揭示 x x x与 y y y间的曲线联系的形式。曲线回归分析最困难和首要的工作是确定自变量与因变量间的曲线关系的类型,曲线回归分析的基本过程:
- 先将 x x x与 ν \nu ν进行变量转换
- 对新变量进行直线回归分析、建立直线回归方程并进行显著性检验和区间估计
- 将新变量还原为原变量,由新变量的直线回归方程和置信区间得出原变量的曲线回归方程和置信区间
由于曲线回归模型种类繁多,所以没有通用的回归方程可直接使用,但是对某些特殊的回归模型,可以通过变量代换、取对数等方法将其线性化,然后使用标准方程求解参数,再将参数带回原方程就是所求。
如有一组数据 x , y x,y x,y数据,画出散点图后显示 x x x与 y y y的变动关系为一条递减的双曲线
设
y ^ = a ^ + b ^ 1 x \widehat{y}=\widehat{a}+\widehat{b}\frac1x y =a +b x1
令 1 x = x ′ \frac1x=x^{\prime} x1=x′,原式变为
y ^ = a ^ + b ^ x ′ \hat{y}=\hat{a}+\hat{b}x^{\prime} y^=a^+b^x′
把原始数据转换为 1 x , y \frac1x,y x1,y, 求解出 a ^ , b ^ \widehat{a},\widehat{b} a ,b ,再把 x ′ = 1 x x^{\prime}=\frac1x x′=x1带入回去得到曲线回归方程
多重共线性:
回归模型中两个或两个以上的自变量彼此相关的现象,多重共线性带来的问题有:
- 回归系数估计值的不稳定增强
- 回归系数假设检验的结果不显著等
多重共线性检验的主要方法:
-
容忍度:
T o l i = 1 − R 2 Tol_{i}=1-R^2 Toli=1−R2- R i R_i Ri是解释变量 x i x_i xi与方程中其他解释变量间的负相关系数
- 容忍度在0~1之间,越接近与0,表示多重共线性越强,越接近于1,表示多重共线性越弱
-
方差膨胀因子(VIF):
V I F i = 1 1 − R i 2 VIF_i=\frac{1}{1-R_i^2} VIFi=1−Ri21- V I F i VIF_i VIFi越大,特别是大于等于10,说明解释变量 x i x_\mathrm{i} xi与方程中其他解释变量之间有严重的多重共线心
- V I F i VIF_i VIFi越接近1,表明解释变量 x i x_\mathrm{i} xi和其他解释变量之间的多重共线性越弱
4.2 配曲线求解
配曲线的一般方法是:
- 画出散点图
- 根据散点图确定须配曲线的类型
- 估计其中的未知参数
4.2.1 常见的六类曲线
-
双曲函数曲线:变形双曲线
方程形式:
{ y ^ = x a + b x y ^ = a + b x x y ^ = 1 a + b x \begin{cases}\widehat{y}=\frac{x}{a+bx}\\\widehat{y}=\frac{a+bx}{x}\\\widehat{y}=\frac{1}{a+bx}\end{cases} ⎩ ⎨ ⎧y =a+bxxy =xa+bxy =a+bx1
图形: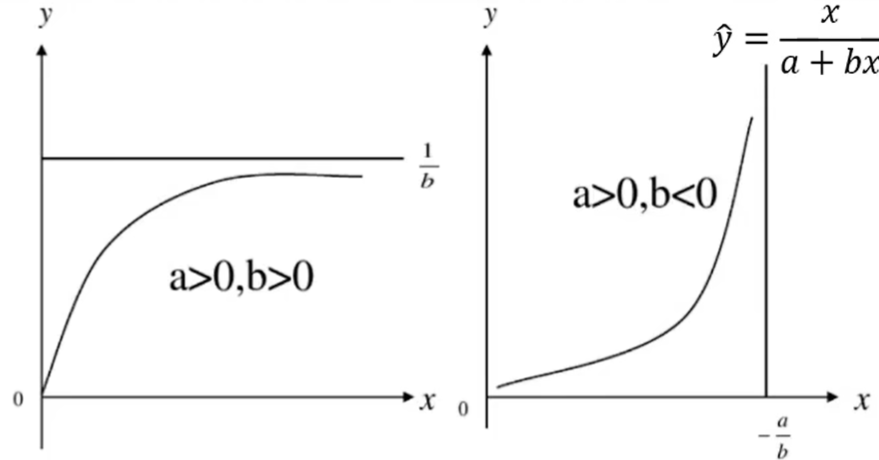
- y ^ = x a + b x \hat{y}=\frac x{a+bx} y^=a+bxx该曲线通过原点(0,0), 当 a > 0 a>0 a>0、 b > 0 b>0 b>0时, y y y随 x x x的增大而增大,但速率趋小,并向 y = 1 b y=\frac1b y=b1 渐进,是凸曲线;当 a > 0 a>0 a>0、 b < 0 b<0 b<0时, y y y随 x x x的增大而增大,速率趋大,并向 x = − a b x=-\frac ab x=−ba渐进,是凹曲线
- 变换方式:
- y ^ = x a + b x \widehat{y}=\frac{x}{a+bx} y =a+bxx,两边取倒数后,令 y ′ = x y ^ y^\prime=\frac x{\hat{y}} y′=y^x,得 y ′ = a x + b y^\prime=ax+b y′=ax+b
- y ^ = a + b x x \hat{y}=\frac{a+bx}x y^=xa+bx,令 y ′ = y ^ x y^\prime=\hat{y}x y′=y^x,得 y ′ = a x + b y^\prime = ax+ b y′=ax+b ; y ^ = 1 a + b x \hat{y} = \frac 1{a+ bx} y^=a+bx1,两边取倒数后,令 y ′ = 1 y y^\prime=\frac1y y′=y1,得 y ′ = a x + b \mathrm{y}^\prime=ax+b y′=ax+b
-
幂函数曲线
方程形式:
y ^ = a x b \hat{y}=ax^{b} y^=axb
图形: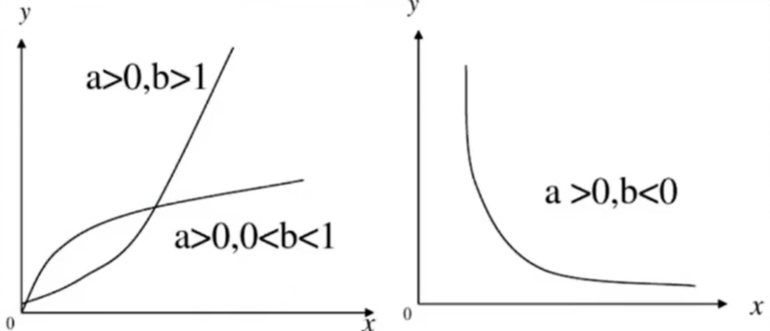
- 当 a > 0 a>0 a>0、 b > 1 b>1 b>1时, y y y随 x x x的增大而增大(增长),是凹曲线;
- 当 a > 0 a>0 a>0、 0 < b < 1 0<b<1 0<b<1时, y y y随 x x x的增大而增大(增长),但变化缓慢,是凸曲线;
- 当 a > 0 a>0 a>0、 b < 0 b<0 b<0时, y y y随 x x x的增大而减小,且以 x , y x,y x,y轴为渐近线,是凹曲线。
- 变换方式:两边取对数,令 y ′ = l n y ^ , x ′ = l n x , a ′ = l n a y^{\prime}=ln\hat{y},x^{\prime}=lnx,a^{\prime}=lna y′=lny^,x′=lnx,a′=lna,得 y ′ = a ′ + b x ′ y^{\prime}=a^{\prime}+bx^{\prime} y′=a′+bx′
-
指数函数曲线
方程形式:
{ y ^ = a e b x y ^ = a b x \left\{\begin{matrix}\widehat{y}=ae^{bx}\\\widehat{y}=ab^x\end{matrix}\right. {y =aebxy =abx
图形: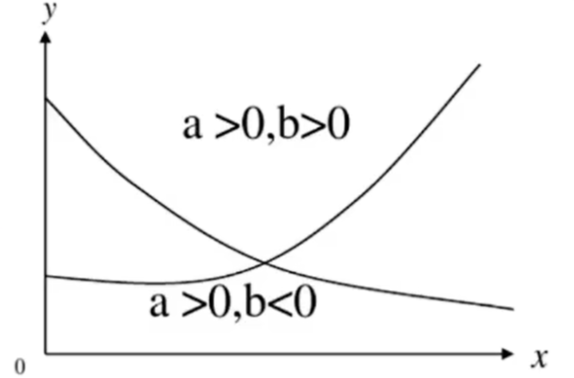
-
y
^
=
a
e
b
x
\hat{y}=ae^{bx}
y^=aebx
- 参数 b b b一般用来描述增长或衰减的速度。
- 当 a > 0 、 b > 0 a>0、b>0 a>0、b>0时, y y y随 x x x的增大而增大(增长),是凹曲线;
- 当 a > 0 、 b < 0 a>0、b<0 a>0、b<0时, y y y随 x x x的增大而减小(衰减),是凹曲线。
- 变换方式:两边取对数,令 y ′ = l n y ^ , a ′ = l n a y^\prime=ln\hat{y},a^{\prime}=lna y′=lny^,a′=lna,得 y ′ = a ′ + b x y^\prime=a^{\prime}+bx y′=a′+bx
-
y
^
=
a
e
b
x
\hat{y}=ae^{bx}
y^=aebx
-
倒指数曲线
方程形式:
y ^ = a e b x , 其中 a > 0 \widehat{y}=ae^{\frac{b}{x}},\text{其中}a>0 y =aexb,其中a>0
图形: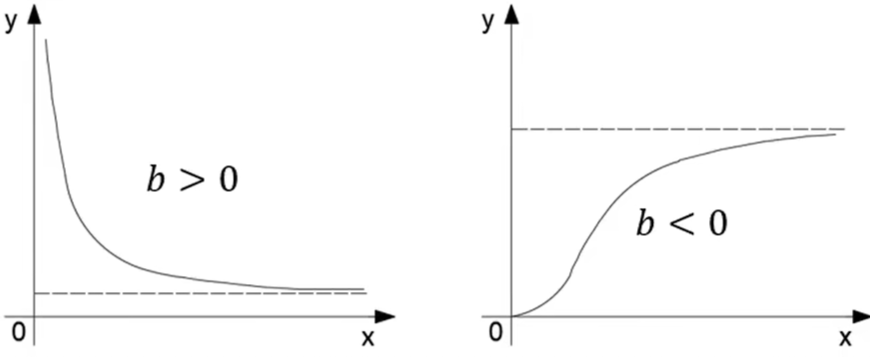
- 当 a > 0 、 b > 0 a>0、b>0 a>0、b>0时, y y y随 x x x的增大而减小(衰减),是凹曲线;
- 当 a > 0 a>0 a>0、 b < 0 b<0 b<0时, y y y随 x x x的增大而增大(增长),是先凹后凸曲线。
- 变换方式:两边取对数,令 y ′ = l n y ^ , a ′ = l n a , x ′ = 1 r y^\prime=ln\hat{y},a^{\prime}=lna,x^{\prime}=\frac1r y′=lny^,a′=lna,x′=r1 ,得 y ′ = a ′ + b x ′ y^\prime=a^{\prime}+bx^{\prime} y′=a′+bx′
-
对数函数曲线
方程形式:
y ^ = a + b l n x ( x > 0 ) \hat{y}=a+blnx(x>0) y^=a+blnx(x>0)
图形: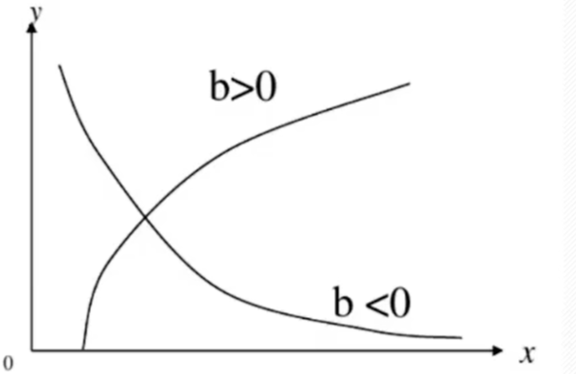
- 对数函数表示:
x
x
x变数的较大变化可引起
y
y
y变数的较小变化。
- b > 0 b>0 b>0时 , y ,y ,y随 x x x的增大而增大,是凸曲线;
- b < 0 b<0 b<0时, y y y随 x x x的增大而减小,是凹曲线。
- 变换方式:令 x ′ = l n x x^\prime=lnx x′=lnx,得 y ^ = a + b x ′ \hat{y}=a+bx^\prime y^=a+bx′
- 对数函数表示:
x
x
x变数的较大变化可引起
y
y
y变数的较小变化。
-
S S S型曲线
- 主要描述动、植物的自然生长过程,又称生长曲线,也可以描述传染病的发展趋势。
- 生长过程的基本特点是开始增长较慢,而在以后的某一范围内迅速增长,达到一定的限度后增长又缓慢下来,曲线呈拉长的’ S ′ S^\prime S′型曲线。著名的 ′ S ′ 'S' ′S′型曲线是Logistic生长曲线。
方程形式:
y ^ = k 1 + a e − b x ( a , b , k 均大于 0 ) x = 0 , y ^ = k 1 + a ; x → ∞ , y ^ = k \hat{y}=\frac{k}{1+ae^{-bx}}(a, b, k\text{均大于}0)\\x=0 ,\hat{y}=\frac{k}{1+a}; x\to\infty ,\hat{y}=k y^=1+ae−bxk(a,b,k均大于0)x=0,y^=1+ak;x→∞,y^=k
图形:
- 所以时间为0的起始量为 1 1 + a \frac{1}{1+a} 1+a1,时间为无限延长的,终极量为 k k k,曲线 x = l n a b x=\frac{lna}b x=blna时有一个拐点,这时 y ^ = k 2 \hat{y}=\frac k2 y^=2k,恰好是终极量的一半拐点左侧,为凹曲线,速率由小趋大;拐点右侧,为凸曲线速率由大趋小。
- 变换方式:两边取倒数再取对数后, y ′ = l n ( k − y ^ y ^ ) , a ′ = l n a y^{\prime}=ln(\frac{k-\hat{y}}{\hat{y}}),a^{\prime}=lna y′=ln(y^k−y^),a′=lna,得 y ′ = a ′ + b x y^{\prime}=a^{\prime}+bx y′=a′+bx
4.2.2 例题求解
出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀,容积不断增大。我们希望知道使用次数与增大的容积之间的关系,对一钢包作试验,测得的数据列于下表:
使用次数 增大容积 使用次数 增大容积 1 / 9 9.99 2 6.42 10 10.49 3 8.20 11 10.59 4 9.58 12 10.60 5 9.50 13 10.80 6 9.70 14 10.60 7 10.00 15 10.90 8 9.93 16 10.76
画出散点图:
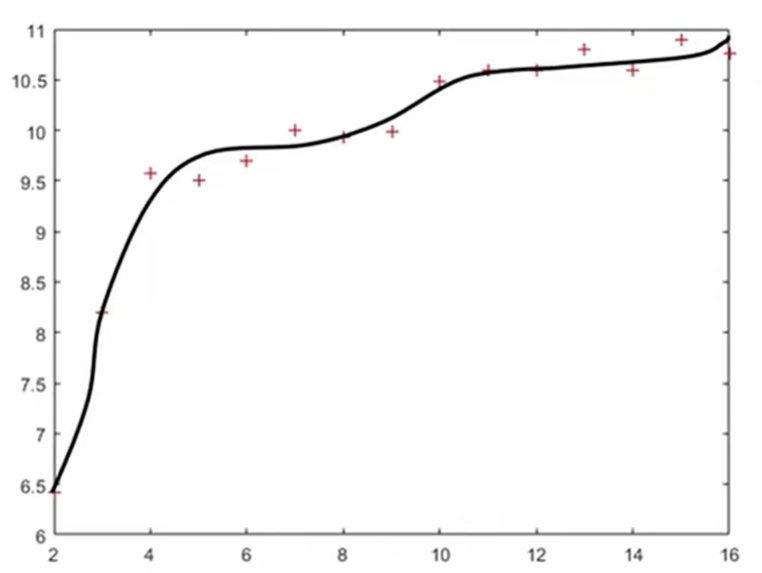
由散点图我们可以选配倒指数曲线
y
=
a
e
b
x
y=ae^{\frac bx}
y=aexb
取对数后得
l
n
y
=
l
n
a
+
b
x
l
n
e
=
l
n
a
+
b
x
lny=lna+\frac{b}{x}lne=lna+\frac{b}{x}
lny=lna+xblne=lna+xb
设
y
^
′
=
l
n
y
,
x
′
=
1
x
,
b
^
=
l
n
a
,
A
^
=
b
\hat{y}^{\prime}=lny ,x^{\prime}=\frac{1}{x} ,\hat{b}=lna ,\hat{A}=b
y^′=lny,x′=x1,b^=lna,A^=b
得
y
^
=
b
^
+
A
^
x
′
\widehat{y}=\widehat{b}+\widehat{A}x^{\prime}
y
=b
+A
x′
利用线性回归的方法,算得
A
^
=
−
1.1107
,
b
^
=
2.4587
a
=
e
b
^
=
11.6789
\begin{aligned}&\hat{A}=-1.1107 ,\widehat{b}=2.4587\\&a=e^{\hat{b}}=11.6789\end{aligned}
A^=−1.1107,b
=2.4587a=eb^=11.6789
所以回归模型为:
y
=
11.6789
e
−
1.1107
x
y=11.6789e^{-\frac{1.1107}{x}}
y=11.6789e−x1.1107
4.3 多项式回归求解
当六类曲线都无法很好地拟合模型时,我们可以使用多项式回归。
设变量
x
x
x、
Y
Y
Y的回归模型为
Y
=
β
0
+
β
1
x
+
β
2
x
2
+
⋯
+
β
p
x
p
+
ϵ
Y=\beta_0+\beta_1x+\beta_2x^2+\cdots+\beta_px^p+\epsilon
Y=β0+β1x+β2x2+⋯+βpxp+ϵ
其中
p
p
p是已知的,
β
i
(
i
=
1
,
2
,
⋯
,
p
)
\beta_i(i=1,2,\cdots,p)
βi(i=1,2,⋯,p)是未知参数,
ϵ
\epsilon
ϵ服从正态分布
N
(
0
,
σ
)
N(0,\sigma)
N(0,σ)
Y
=
β
0
+
β
1
x
+
β
2
x
2
+
⋯
+
β
p
x
p
Y=\beta_0+\beta_1x+\beta_2x^2+\cdots+\beta_px^p
Y=β0+β1x+β2x2+⋯+βpxp
称为回归多项式,上面的回归模型称为多项式回归。
4.3.1 一元多项式回归
matlab求解方法:
y
=
a
1
x
m
+
a
2
x
m
−
1
+
⋯
+
a
m
x
+
a
m
+
1
y=a_{1}x^{m}+a_{2}x^{m-1}+\cdots+a_{m}x+a_{m+1}
y=a1xm+a2xm−1+⋯+amx+am+1
-
回归:
-
确定多项式系数的命令 :
[ p , S ] = p o l y f i t ( x , y , m ) [ p , S] = polyfit( x , y , m) [p,S]=polyfit(x,y,m)
其中 x = ( x 1 , x 2 , . . . , x n ) , y = ( y 1 , y 2 , . . . , y n ) ; p = ( a 1 , a 2 , ⋯ , a m + 1 ) x=(x_1,x_{2},...,x_{n}),y=(y_{1},y_{2},...,y_{n});p=(a_1,a_2,\cdots,a_{m+1}) x=(x1,x2,...,xn),y=(y1,y2,...,yn);p=(a1,a2,⋯,am+1)是多项式 y = a 1 x m + a 2 x m − 1 + ⋯ + a m x + a m + 1 y=a_1x^m+a_2x^{m-1}+\cdots+a_mx+a_{m+1} y=a1xm+a2xm−1+⋯+amx+am+1的系数; S S S是一个结构数据,用来估计预测误差 -
一元多项式回归命令: p o l y t o o l ( x , y , m ) polytool(x,y,m) polytool(x,y,m)
-
-
预测和预测误差估计:
-
Y = p o l y v a l ( p , x ) Y=polyval(p,x) Y=polyval(p,x) 求 p o l y f i t polyfit polyfit所得的回归多项式在 x x x处预测值 Y ; Y; Y;
-
[ Y , D E L T A ] = p o l y c o n f ( p , x , S , a l p h a ) [Y,DELTA]=polyconf(p,x,S,alpha) [Y,DELTA]=polyconf(p,x,S,alpha)
求 p o l y f i t polyfit polyfit所得的回归多项式在 x x x处的预测值 Y Y Y及预测值的显著性为 a l p h a alpha alpha的置信区间
Y ± D E L T A , a l p h a Y\pm DELTA,alpha Y±DELTA,alpha缺省时为0.05
-
示例:
观测物体降落的距离s与时间 t t t的关系,得到数据如下表,求s关于 t t t的回归方程
s ^ = a + b t + c t 2 \hat{s}=a+bt+ct^{2} s^=a+bt+ct2
t ( s ) t(s) t(s) 1/30 2/30 3/30 4/30 5/30 6/30 7/30 s ( c m ) s(cm) s(cm) 11.86 15.67 20.60 26.69 33.71 41.93 51.13
t ( s ) t(s) t(s) 8/30 9/30 10/30 11/30 12/30 13/30 14/30 s ( c m ) s(cm) s(cm) 61.49 72.90 85.44 99.08 113.77 129.54 146.48
方法一:直接作多项式回归
clc
clear
t=1/30:1/30:14/30;
s = [11.86, 15.67, 20.60, 26.69, 33.71, 41.93, 51.13, 61.49, 72.90, 85.44, 99.08, 113.77, 129.54, 146.48];
[p,S]=polyfit(t,s,2);% 进行二次多项式拟合
% 预测及作图
Y=polyconf(p,t,S); % 计算拟合曲线的预测值
plot(t,s,'k+',t,Y,'r'); % 绘制原始数据点和拟合曲线
xlabel('t')
ylabel('s')
title('二次多项式回归')
legend("原始数据","拟合曲线")
结果:
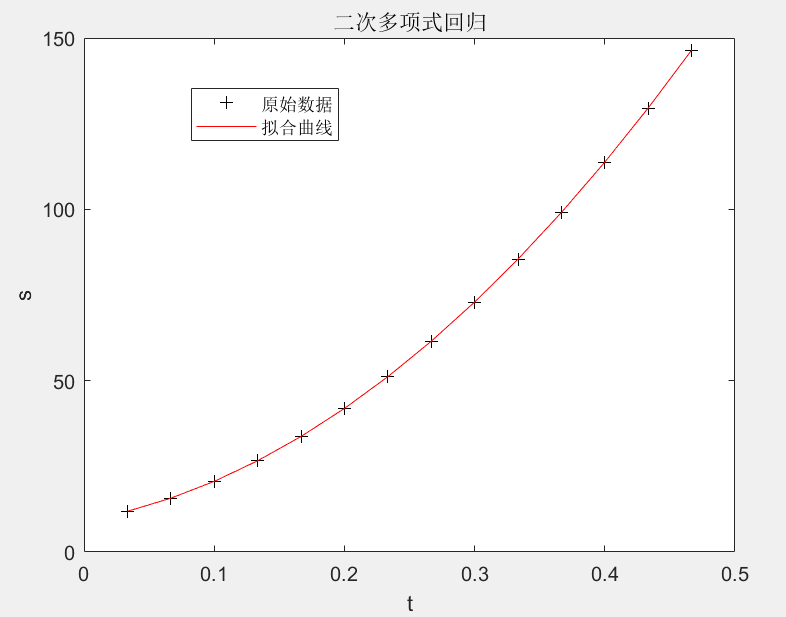
方法二:化为多元线性回归
clc
clear
t=1/30:1/30:14/30;
s = [11.86, 15.67, 20.60, 26.69, 33.71, 41.93, 51.13, 61.49, 72.90, 85.44, 99.08, 113.77, 129.54, 146.48];
% 令x1=t,x2=t^2
T=[ones(14,1),t',(t.^2)'];
[b,bint,r,rint,stats]=regress(s',T);
b
输出:
b =
9.1329
65.8896
489.2946
4.3.2 多元二项式回归
matlab求解方法:
命令: r s t o o l ( x , y , m o d e l ′ , a l p h a ) rstool(x,y,model',alpha) rstool(x,y,model′,alpha)
x x x—— n n n(样本个数) × m \times m ×m(自变量个数)矩阵
y y y—— n n n(样本个数)维向量
a l p h a alpha alpha——显著性水平(默认0.05)
m
o
d
e
l
model
model——由下列4个模型中选择1个(用字符串输入,缺省时为线性模型)
l
i
n
e
a
r
(
线性
)
:
y
=
β
0
+
β
1
x
1
+
⋯
+
β
m
x
m
p
u
r
e
q
u
a
d
r
a
t
i
c
(
纯二次
)
:
y
=
β
0
+
β
1
x
1
+
⋯
+
β
m
x
m
+
∑
j
=
1
n
β
j
j
x
j
2
i
n
t
e
r
a
c
t
i
o
n
(
交叉
)
:
y
=
β
0
+
β
1
x
1
+
⋯
+
β
m
x
m
+
∑
1
≤
j
≠
k
≤
m
β
j
k
x
j
x
k
q
u
a
d
r
a
t
i
c
(
完全二次
)
:
y
=
β
0
+
β
1
x
1
+
⋯
+
β
m
x
m
+
∑
1
≤
j
,
k
≤
m
β
j
k
x
j
x
k
\begin{aligned} &linear(\text{线性})\colon y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{m}x_{m} \\ &purequadratic(\text{纯二次})\colon y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{m}x_{m}+\sum_{j=1}^{n}\beta_{jj}x_{j}^{2} \\ &interaction(\text{交叉})\colon y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{m}x_{m}+\sum_{1\leq j\neq k\leq m}\beta_{jk}x_{j}x_{k} \\ &quadratic(\text{完全二次})\colon y=\beta_{0}+\beta_{1}x_{1}+\cdots+\beta_{m}x_{m}+\sum_{1\leq j ,k\leq m}\beta_{jk}x_{j}x_{k} \end{aligned}
linear(线性):y=β0+β1x1+⋯+βmxmpurequadratic(纯二次):y=β0+β1x1+⋯+βmxm+j=1∑nβjjxj2interaction(交叉):y=β0+β1x1+⋯+βmxm+1≤j=k≤m∑βjkxjxkquadratic(完全二次):y=β0+β1x1+⋯+βmxm+1≤j,k≤m∑βjkxjxk
示例:
设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量
需求量 100 75 80 70 50 65 90 100 110 60 收入 1000 600 1200 500 300 400 1300 1100 1300 300 价格 5 7 6 6 8 7 5 4 3 9
选择纯二次模型,即 y = β 0 + β 1 x 1 + β 2 x 2 + β 11 x 1 2 + β 22 x 2 2 y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_{11}x_1^2+\beta_{22}x_2^2 y=β0+β1x1+β2x2+β11x12+β22x22
x1 = [1000, 600, 1200, 500, 300, 400, 1300, 1100, 1300, 300];
x2= [5, 7, 6, 6, 8, 7, 5, 4, 3, 9];
y= [100, 75, 80, 70, 50, 65, 90, 100, 110, 60];
x=[x1',x2'];
rstool(x,y,'purequadratic')
beta,rmse
选择 x 1 x1 x1和 x 2 x2 x2的值进行预测
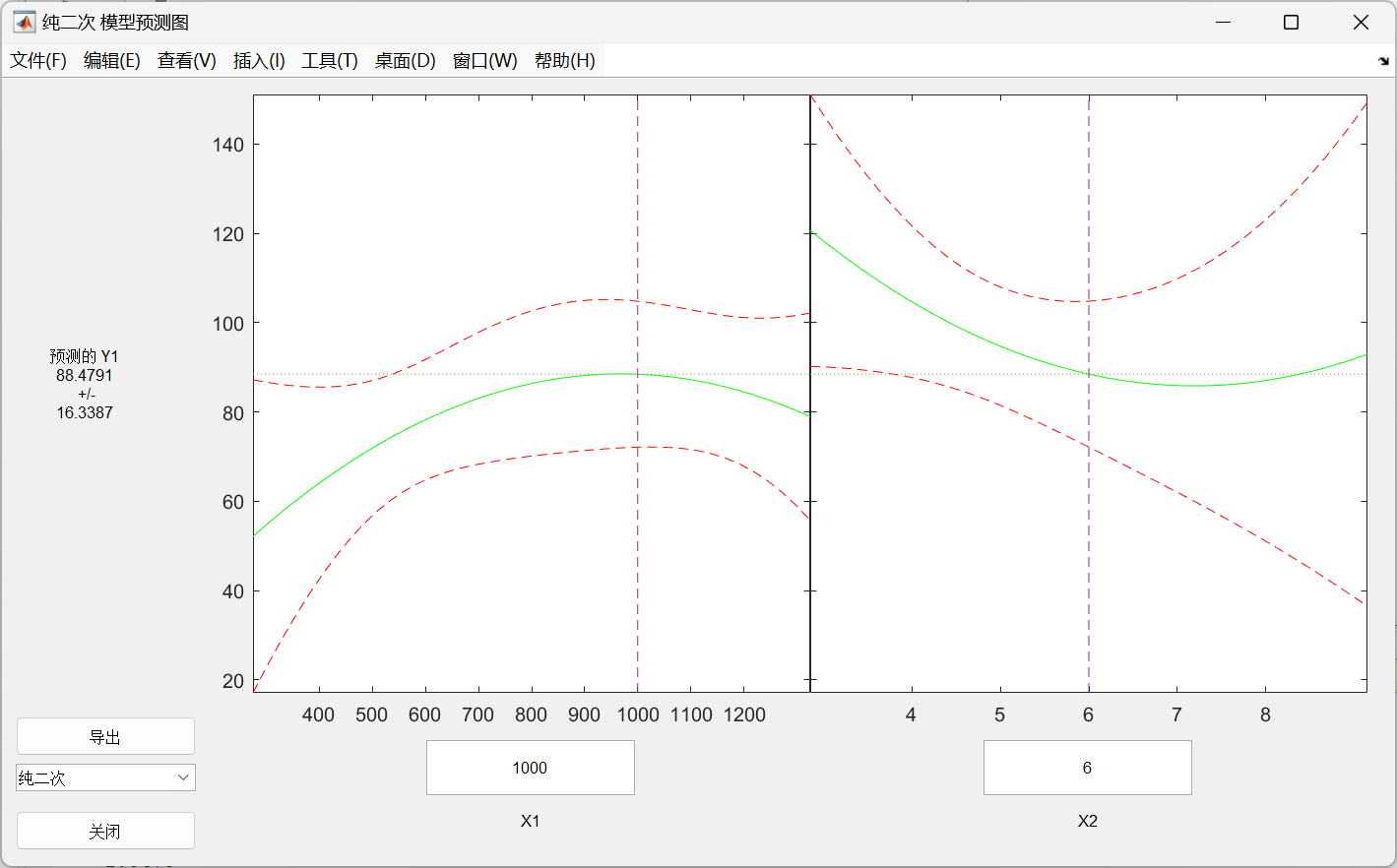
输出:
beta =
110.5313
0.1464
-26.5709
-0.0001
1.8475
rmse =
4.5362
方法二:化为多元线性回归
x1 = [1000, 600, 1200, 500, 300, 400, 1300, 1100, 1300, 300];
x2= [5, 7, 6, 6, 8, 7, 5, 4, 3, 9];
y= [100, 75, 80, 70, 50, 65, 90, 100, 110, 60]';
% 令x3=x1^2; x4=x2^2
X=[ones(10,1),x1',x2',(x1.^2)',(x2.^2)'];
[b,bint,r,rint,stats]=regress(y,X);
b,stats
结果:
b =
110.5313
0.1464
-26.5709
-0.0001
1.8475
stats =
0.9702 40.6656 0.0005 20.5771
4.4 一般求解
-
回归命令
-
确定回归系数的命令:
[ b e t a , r , J ] = n l i n f i t ( x , y , ′ m o d e l ′ , b e t a 0 ) [beta,r,J]=nlinfit(x,y,'model',beta0) [beta,r,J]=nlinfit(x,y,′model′,beta0)
b e t a beta beta——估计出的回归系数
r r r——残差
J J J—— J a c o b i a n Jacobian Jacobian矩阵
x , y x,y x,y——输入数据 x , y x,y x,y分别为 n × m n\times m n×m矩阵和 n n n维列向量,对一元非线性回归, x x x为 n n n维列向量
′ m o d e l ′ 'model' ′model′——是事先用 m m m文件定义的非线性函数
b e t a 0 beta0 beta0——回归系数的初值 -
非线性回归命令: n l i n t o o l ( x , y , ′ m o d e l ′ , b e t a 0 , a l p h a ) nlintool(x,y,'model',beta0,alpha) nlintool(x,y,′model′,beta0,alpha)
-
-
预测和预测误差估计
[ Y , D E L T A ] = n l p r e d c i ( ′ m o d e l ′ , x , b e t a , r , J ) [Y,DELTA]=nlpredci(^{\prime}model^{\prime},x,beta,r,J) [Y,DELTA]=nlpredci(′model′,x,beta,r,J)
求 n l i n f i t nlinfit nlinfit或 n l i n t o o l nlintool nlintool所得的回归函数在 x x x处的预测值 Y Y Y及预测值的显著性为 a l p h a alpha alpha的置信区间$ Y\pm DELTA $
示例:
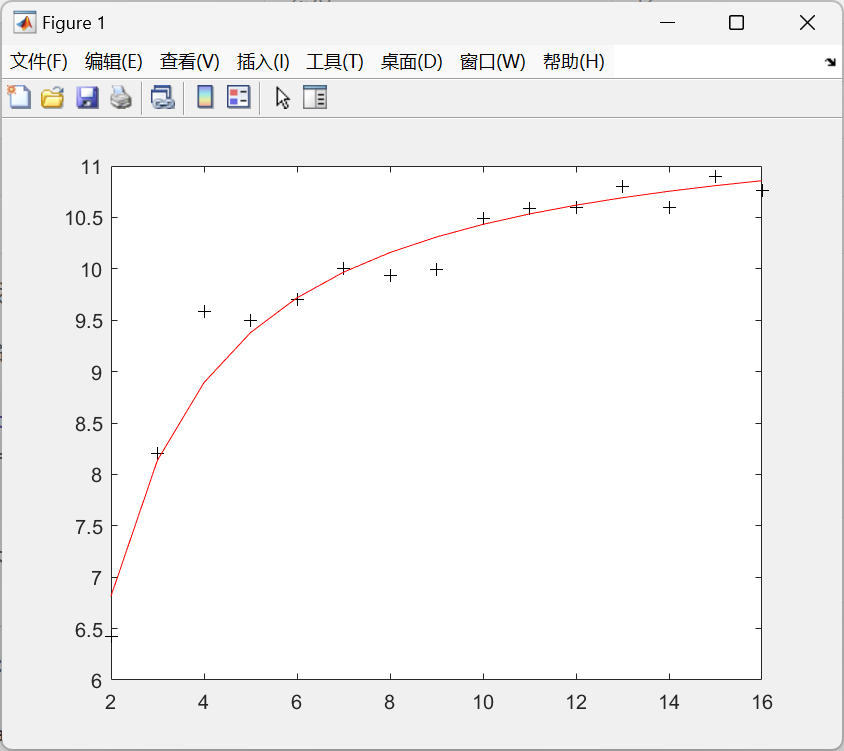
出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀,容积不断增大。我们希望知道使用次数与增大的容积之间的关系,对一钢包作试验,测得的数据列于下表:
使用次数 增大容积 使用次数 增大容积 1 / 9 9.99 2 6.42 10 10.49 3 8.20 11 10.59 4 9.58 12 10.60 5 9.50 13 10.80 6 9.70 14 10.60 7 10.00 15 10.90 8 9.93 16 10.76
由散点图我们可以选配倒指数曲线 y = a e b x y=ae^{\frac bx} y=aexb。
对将要拟合的非线性模型 y = a e b x y=ae^{\frac bx} y=aexb,建立 v o l u m . m volum.m volum.m文件
function yhat=volum(beta,x)
yhat=beta(1)*exp(beta(2)./x);
end
主函数如下
% 输入数据
x=2:16;
y = [ 6.42, 8.20, 9.58, 9.50, 9.70, 10.00, 9.93, 9.99, 10.49, 10.59, 10.60, 10.80, 10.60, 10.90, 10.76];
beta0=[8 2]';
% 求回归系数
[beta,r,j]=nlinfit(x',y','volum',beta0);
beta
% 预测及作图
[YY delta]=nlpredci('volum',x',beta,r,j);
plot(x,y,'k+',x,YY,'r')
输出:
beta =
11.6037
-1.0641