代码随想录算法训练营第五十八天 | 拓扑排序精讲-软件构建
目录
软件构建
思路
拓扑排序的背景
拓扑排序的思路
模拟过程
判断有环
写代码
方法一: 拓扑排序
软件构建
- 题目链接:卡码网:117. 软件构建
文章讲解:代码随想录
某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
输入描述:
第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。
后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
输出描述:
输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
如果不能成功处理(相互依赖),则输出 -1。
输入示例:
5 4 0 1 0 2 1 3 2 4输出示例:
0 1 2 3 4
提示信息:
文件依赖关系如下:
所以,文件处理的顺序除了示例中的顺序,还存在
0 2 4 1 3
0 2 1 3 4
等等合法的顺序。
数据范围:
- 0 <= N <= 10 ^ 5
- 1 <= M <= 10 ^ 9
思路
拓扑排序的背景
本题是拓扑排序的经典题目。
一聊到 拓扑排序,一些录友可能会想这是排序,不会想到这是图论算法。
其实拓扑排序是经典的图论问题。
先说说 拓扑排序的应用场景。
大学排课,例如 先上A课,才能上B课,上了B课才能上C课,上了A课才能上D课,等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。
拓扑排序在文件处理上也有应用,我们在做项目安装文件包的时候,经常发现 复杂的文件依赖关系, A依赖B,B依赖C,B依赖D,C依赖E 等等。
如果给出一条线性的依赖顺序来下载这些文件呢?
有录友想上面的例子都很简单啊,我一眼能给排序出来。
那如果上面的依赖关系是一百对呢,一千对甚至上万个依赖关系,这些依赖关系中可能还有循环依赖,你如何发现循环依赖呢,又如果排出线性顺序呢。
所以 拓扑排序就是专门解决这类问题的。
概括来说,给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序。
当然拓扑排序也要检测这个有向图 是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。
所以拓扑排序也是图论中判断有向无环图的常用方法。
拓扑排序的思路
拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是广搜也可能是深搜。
大家可能发现 各式各样的解法,纠结哪个是拓扑排序?
其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。
实现拓扑排序的算法有两种:卡恩算法(BFS)和DFS
卡恩1962年提出这种解决拓扑排序的思路
一般来说我们只需要掌握 BFS (广度优先搜索)就可以了,清晰易懂,如果还想多了解一些,可以再去学一下 DFS 的思路,但 DFS 不是本篇重点。
接下来我们来讲解BFS的实现思路。
以题目中示例为例如图:
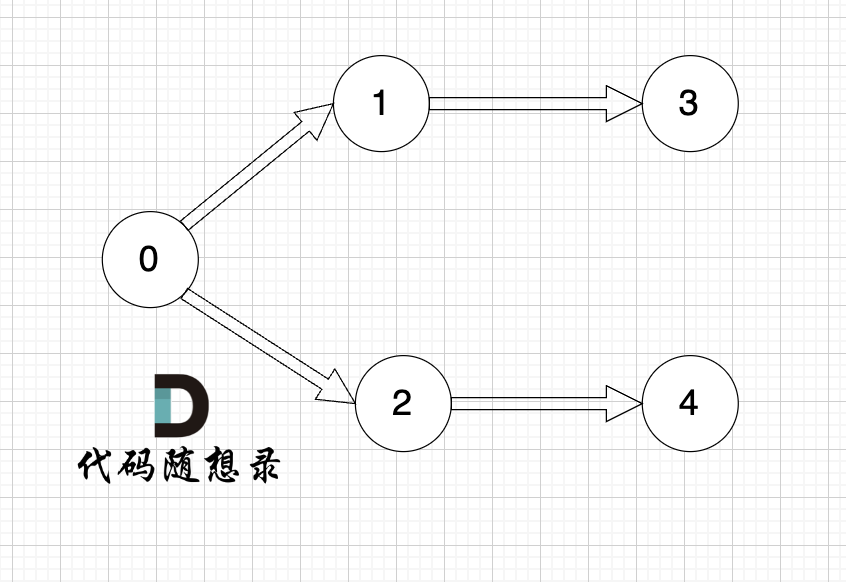
做拓扑排序的话,如果肉眼去找开头的节点,一定能找到 节点0 吧,都知道要从节点0 开始。
但为什么我们能找到 节点0呢,因为我们肉眼看着 这个图就是从 节点0出发的。
作为出发节点,它有什么特征?
你看节点0 的入度 为0 出度为2, 也就是 没有边指向它,而它有两条边是指出去的。
节点的入度表示 有多少条边指向它,节点的出度表示有多少条边 从该节点出发。
所以当我们做拓扑排序的时候,应该优先找 入度为 0 的节点,只有入度为0,它才是出发节点。 理解以上内容很重要!
接下来我给出 拓扑排序的过程,其实就两步:
- 找到入度为0 的节点,加入结果集
- 将该节点从图中移除
循环以上两步,直到 所有节点都在图中被移除了。
结果集的顺序,就是我们想要的拓扑排序顺序 (结果集里顺序可能不唯一)
模拟过程
用本题的示例来模拟这一过程:
1、找到入度为0 的节点,加入结果集
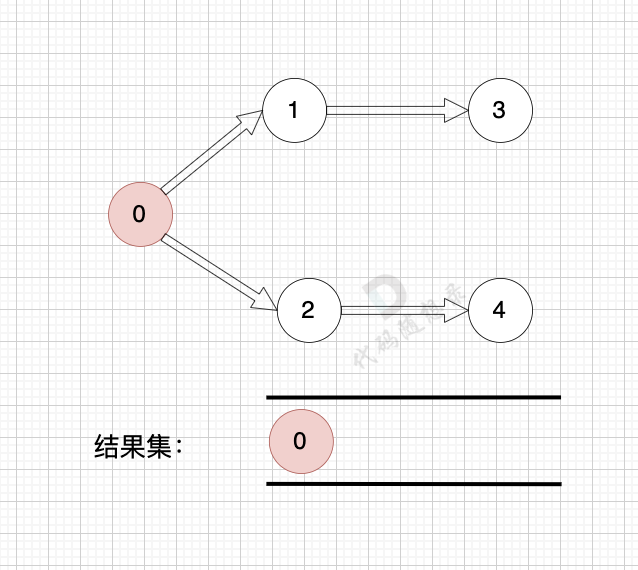
2、将该节点从图中移除
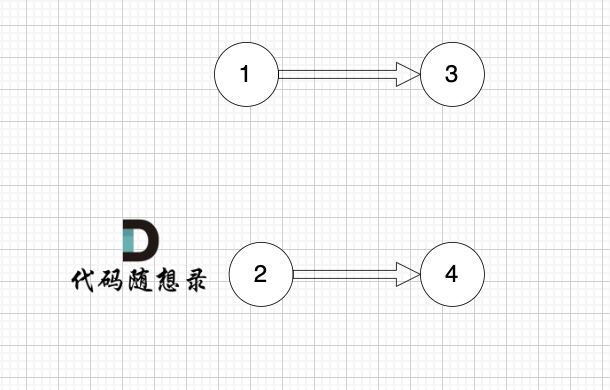
1、找到入度为0 的节点,加入结果集
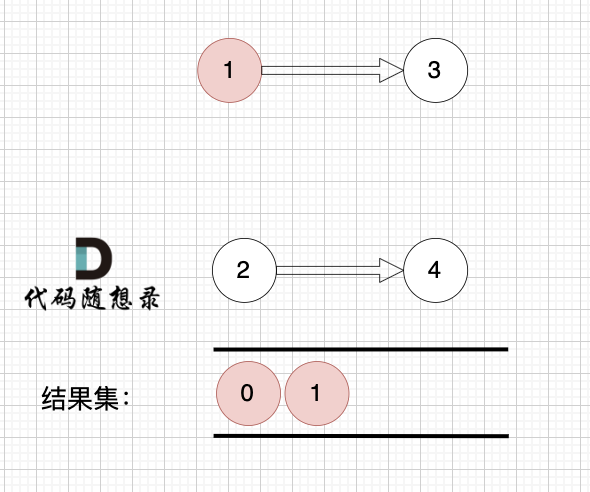
这里大家会发现,节点1 和 节点2 入度都为0, 选哪个呢?
选哪个都行,所以这也是为什么拓扑排序的结果是不唯一的。
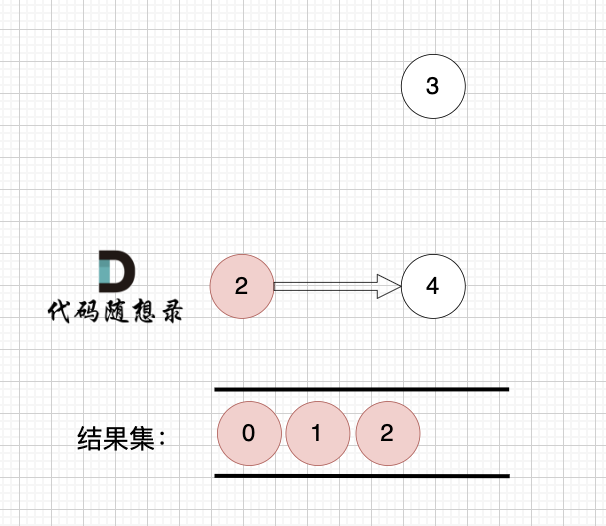
2、将该节点从图中移除
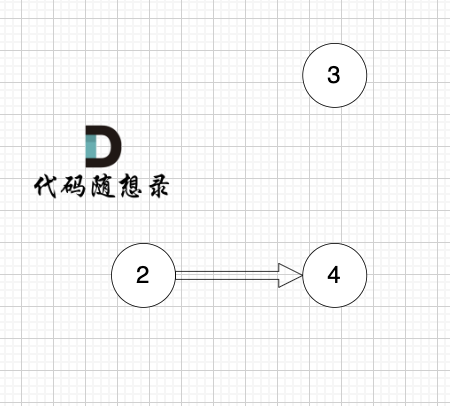
1、找到入度为0 的节点,加入结果集
节点2 和 节点3 入度都为0,选哪个都行,这里选节点2
2、将该节点从图中移除

后面的过程一样的,节点3 和 节点4,入度都为0,选哪个都行。
最后结果集为: 0 1 2 3 4 。当然结果不唯一的。
判断有环
如果有 有向环怎么办呢?例如这个图:
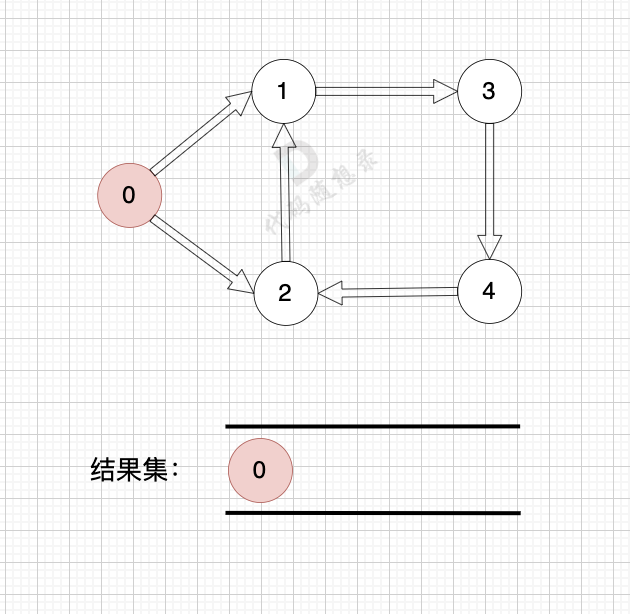
这个图,我们只能将入度为0 的节点0 接入结果集。
之后,节点1、2、3、4 形成了环,找不到入度为0 的节点了,所以此时结果集里只有一个元素。
那么如果我们发现结果集元素个数 不等于 图中节点个数,我们就可以认定图中一定有 有向环!
这也是拓扑排序判断有向环的方法。
通过以上过程的模拟大家会发现这个拓扑排序好像不难,还有点简单。
写代码
理解思想后,确实不难,但代码写起来也不容易。
为了每次可以找到所有节点的入度信息,我们要在初始化的时候,就把每个节点的入度 和 每个节点的依赖关系做统计。
代码如下:
# 记录每个文件的入度
inDegree = [0] * n
# 记录文件的依赖关系
ucamp = defaultdict(list)
# s->t,先有s才能有t
for s,t in edges:
#t的入度加一
inDegree[t] += 1
# 记录s指向哪些文件
ucamp[s].append(t)找入度为0 的节点,我们需要用一个队列放存放。
因为每次寻找入度为0的节点,不一定只有一个节点,可能很多节点入度都为0,所以要将这些入度为0的节点放到队列里,依次去处理。
代码如下:
# 初始化队列,加入入度为0的节点
que = deque([i for i in range(len(inDegree)) if inDegree[i] == 0])开始从队列里遍历入度为0 的节点,将其放入结果集。
while que:
# 当前选中的文件
cur = que.popleft()
result.append(cur)
这里面还有一个很重要的过程,如何把这个入度为0的节点从图中移除呢?
首先我们为什么要把节点从图中移除?
为的是将 该节点作为出发点所连接的边删掉。
删掉的目的是什么呢?
要把 该节点作为出发点所连接的节点的 入度 减一。
如果这里不理解,看上面的模拟过程第一步:

这事节点1 和 节点2 的入度为 1。
将节点0删除后,图为这样:
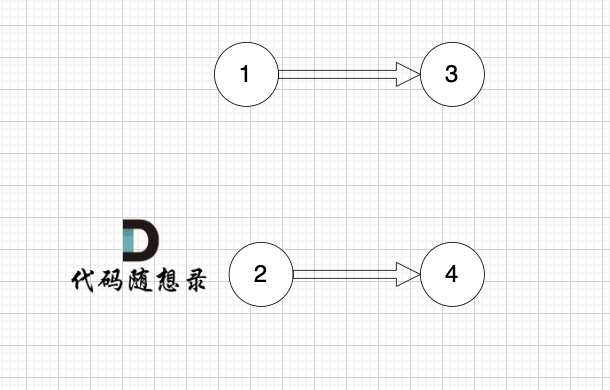
那么 节点0 作为出发点 所连接的节点的入度 就都做了 减一 的操作。
此时 节点1 和 节点 2 的入度都为0, 这样才能作为下一轮选取的节点。
所以,我们在代码实现的过程中,本质是要将 该节点作为出发点所连接的节点的 入度 减一 就可以了,这样好能根据入度找下一个节点,不用真在图里把这个节点删掉。
方法一: 拓扑排序
from collections import deque, defaultdict
def topological_sort(n, edges):
inDegree = [0] * n # inDegree 记录每个文件的入度
umap = defaultdict(list) # 记录文件依赖关系
# 构建图和入度表
for s, t in edges:
inDegree[t] += 1
umap[s].append(t)
# 初始化队列,加入所有入度为0的节点
queue = deque([i for i in range(n) if inDegree[i] == 0])
result = []
while queue:
cur = queue.popleft() # 当前选中的文件
result.append(cur)
for file in umap[cur]: # 获取该文件指向的文件
inDegree[file] -= 1 # cur的指向的文件入度-1
if inDegree[file] == 0:
queue.append(file)
if len(result) == n:
print(" ".join(map(str, result)))
else:
print(-1)
if __name__ == "__main__":
n, m = map(int, input().split())
edges = [tuple(map(int, input().split())) for _ in range(m)]
topological_sort(n, edges)