快速排序
一：基本思想
任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右
子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
思想解释：
1：确认一个基准值，一般默认最左面的值
2：通过 排序函数，最后会使得该基准值停留在正确的位置，并且基准值左面的值都小于基准值，基准值的右面的值都大于基准值(排序函数会遍历整个数组，所以时间复杂度为O(N))
3：然后该数所处的位置就不用管了，然后递归用 排序函数 解决该数所处位置的左右两个数组
4：最后得到一个有序数组
分割数组的两种情况：
理想情况：
解释：该种情况是一种理想的情况
我们每次在最左取的基准值，在经过 排序函数 之后，都会停留在数组的中间位置，这样的话，一个元素总数为N的数组，会被分为logN层，每层的时间复杂度为O(N)，总的复杂度就是O（N*logN）。
极端情况：
解释： 该种情况是一种极端的情况
我们每次在最左取的基准值，在经过 排序函数 之后，还是停留在原地，按照这种极端情况，没有递归解决左右数组这一说了，数组只会呈-1的递减，每次都只是递归解决基准值右面的数组，所以这个数组被分为N层，每层的时间复杂度为O(N)，总的复杂度就是O（N^2）。
那理想情况我们也不可能取到，又要避免极端情况，这时候，就需要三数取中了。
二：三数取中的意义
解释：
- 选择三个元素：通常选择数组的第一个元素、最后一个元素以及位于中间的元素。
- 计算中位数：比较这三个元素，找到它们的中位数。
- 交换基准：将中位数与数组的第一个元素（或最后一个元素）交换，使得中位数成为基准元素。
这样的话就能避免极端情况了,虽然达不到理想的情况，但是时间复杂度和理想情况的同一个量级
代码：
int GetMidi(int* a, int left, int right)
{
// 计算中间元素的下标
int mid = (left + right) / 2;
// 比较三个元素：left, mid, right
// 首先比较left和mid
if (a[left] < a[mid])
{
// 如果left < mid，再比较mid和right
if (a[mid] < a[right])
{
// 如果left < mid < right，则mid是中间值
return mid;
}
else if (a[left] > a[right]) // 如果left > right，则mid是最大值
{
// 在这种情况下，left是中间值
return left;
}
else
{
// 如果left < right，则right是中间值
return right;
}
}
else // 如果a[left] > a[mid]
{
// 比较mid和right
if (a[mid] > a[right])
{
// 如果mid > right，则mid是中间值
return mid;
}
else if (a[left] < a[right]) // 如果left < right，则mid是最小值
{
// 在这种情况下，left是中间值
return left;
}
else
{
// 如果left > right，则right是中间值
return right;
}
}
}三：排序函数（单趟）的三种方法
1：Hoare法
解释：
1：因为最后的6会处于正确的位置，6的左面的值都<6。所以left向右走的时候，肯定是找>6的值，right向左走的时候，肯定是找<6的值，二者都找到了，L一定会找到<6的，R也一定会找到>6de,二者不可能存在只有L或者只有R找到的情况，因为三数取中已经让基准值避免了取到最大或者最小的这种极端情况，所以二者都会找到，然后彼此交换
2：最后直到left = right 代表二者相遇，此时退出循环
3：将基准值 6 放到正确的位置 也就是相遇的位置
4：返回基准值6的位置，这样才能分开数组，去递归基准值左右的数组
相遇的疑问：
Q1：为什么相遇坐标的值，一定能和基准值交换，也就是说为什么能保证相遇坐标的值，一定比基准值6小？
A1：右面R先走做到的
右面R先走，此时相遇可以分为两种情况：
第一种：L走到R处相遇
因为R先走，所以要满足第一种情况L走到R处相遇，一定是在某一次寻找中，R找到了比基准值小的值，然后停下，此时L找不到比key大的，最后和R相遇，此时相遇处也就是R之前找到的比基准值小的位置，所以此时一定是可以和基准值进行交换的
第二种：R走到L处相遇
在某一次寻找中，R开始找比基准值小的值，但是一直没有找到，直到走到了L处与其相遇，此时的L处一定不会是最左面，因为三数取中后，L肯定在上一轮中向右走并且找到了比基准值大的值，然后R也在上一轮中找到了比基准值小的值，L和R进行了交换（L处的值是R找到的比基准值小的值），所以此一轮中的R走到L处与其相遇，相遇位置处也就是L处的值，一定是比基准值小的，所以此时一定是可以和基准值进行交换的。
代码：
int PartSort1(int* a, int left, int right)
{
// 使用三数取中法获取基准元素的正确位置
int Mid = GetMidi(a, left, right);
// 将基准元素交换到数组的最左边
Swap(&a[left], &a[Mid]);
// 设置基准元素的索引为keyi
int keyi = left;
// 当left小于right时，进行单趟排序
while (left < right)
{
// 从右向左扫描，找到第一个小于基准元素的值
while (left < right && a[right] >= a[keyi])
{
right--;
}
// 注意，这里使用&&连接两个条件，并且顺序很重要，
// 因为如果left >= right，我们就不再需要继续比较
// 此时a[right] >= a[keyi]放在前面的话，会越界访问
// 从左向右扫描，找到第一个大于基准元素的值
while (left < right && a[left] <= a[keyi])
{
left++;
}
// 交换两个元素，将大于基准的元素放到右边，小于基准的元素放到左边
Swap(&a[left], &a[right]);
}
// 最后，将基准元素放到正确的位置（left此时指向的位置）
Swap(&a[keyi], &a[left]);
// 返回基准元素的最终位置
return left;
}内部while循环的条件疑问：
Q2：最外面的while条件有了left < right，为什么内部循环的while里面还有left < right？
A2:因为如果内部循环while没有left < right的话，那么一直找不到会越界，最外面的while只能判断一次，无法彻底控制，所以循环里面的while里面应该是：left<right && a【right】>=key
Q3：为什么内部循环的while条件是<=和>=而不是单纯的<和>
A3：相等的值交换没有意义，会造成死循环，因为交换之后，当前位置的值会继续判断，才会往下走，如果相同的值当需要交换，那交换之后还是会重复的交换，所以应该是>=和<=
总结：
升序排序
-
基准值放在最左面：
right指针先移动，寻找小于基准值的元素（因为我们要把小于基准值的元素放到左边）。left指针后移动，寻找大于基准值的元素（因为我们要把大于基准值的元素放到右边）。
-
基准值放在最右面：
left指针先移动，寻找大于基准值的元素（因为我们要把大于基准值的元素放到右边）。right指针后移动，寻找小于基准值的元素（因为我们要把小于基准值的元素放到左边）。
降序排序
-
基准值放在最左面：
right指针先移动，寻找大于基准值的元素（因为我们要把大于基准值的元素放到左边）。left指针后移动，寻找小于基准值的元素（因为我们要把小于基准值的元素放到右边）。
-
基准值放在最右面：
left指针先移动，寻找小于基准值的元素（因为我们要把小于基准值的元素放到右边）。right指针后移动，寻找大于基准值的元素（因为我们要把大于基准值的元素放到左边）。
2：挖坑法
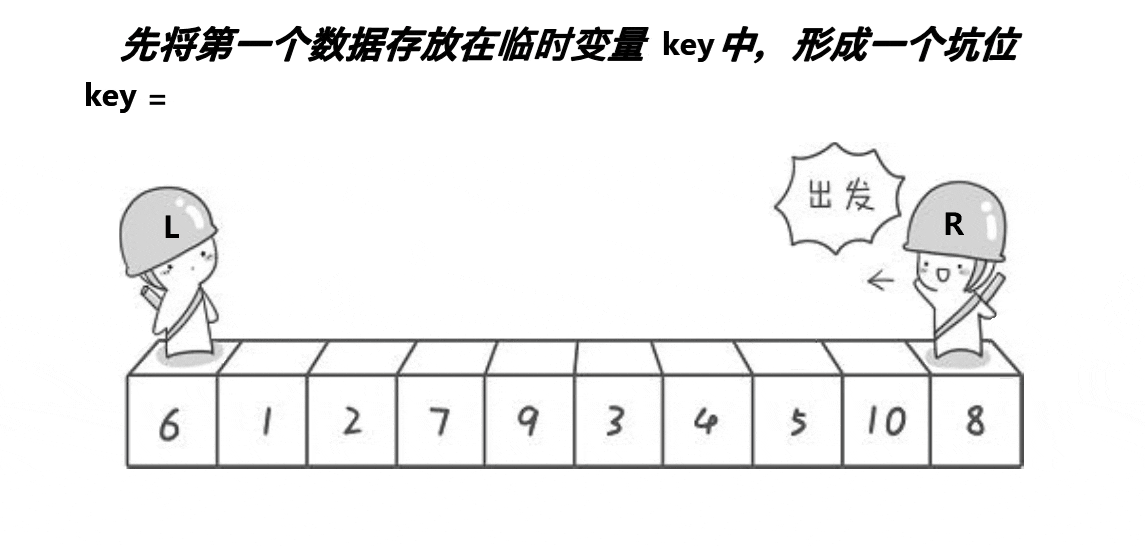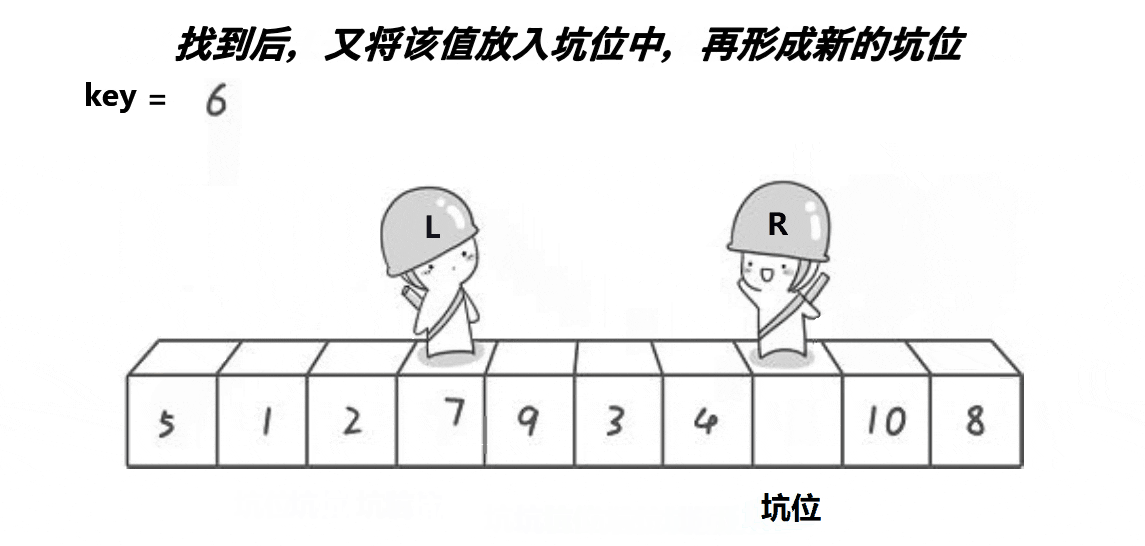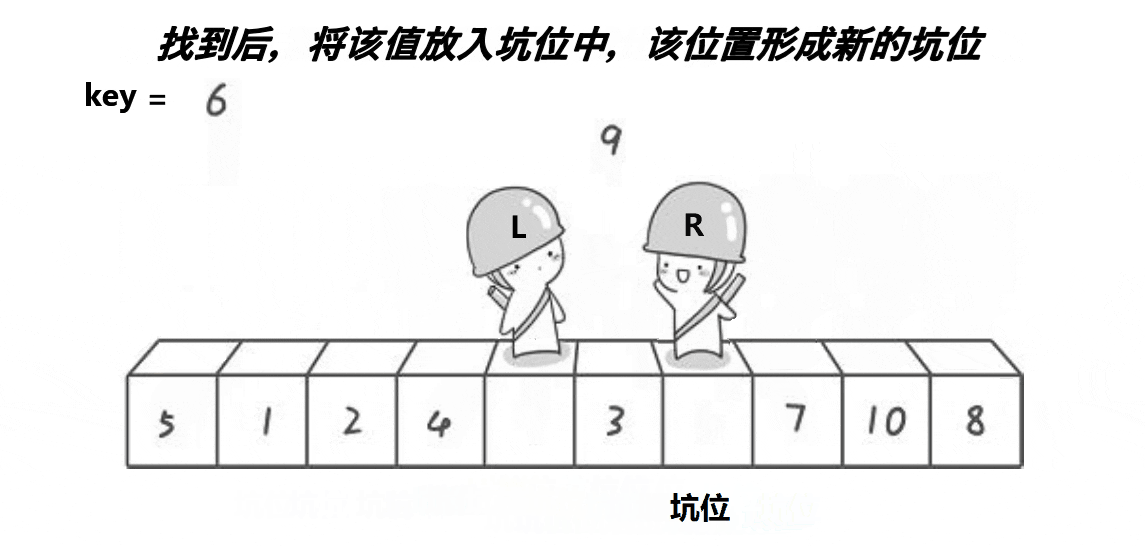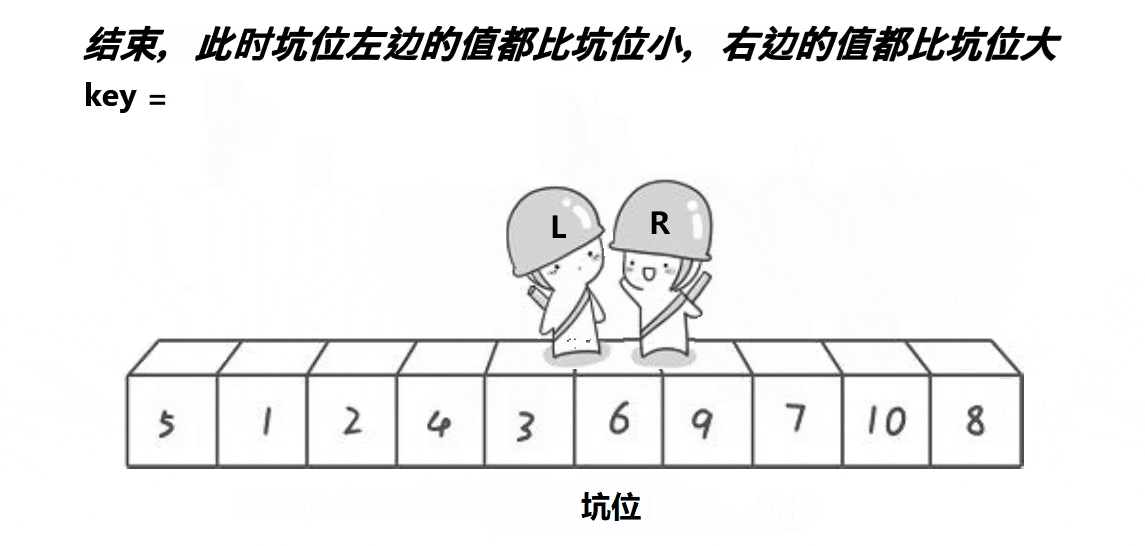
解释：
1：基准值得先保存到一个临时变量key中，而且初识基准值的下标要保存到一个临时变量hole（坑位）中
2：依旧是R先走找小，找到了就把该值放进下标为hole的位置上，不用担心覆盖掉hole位置的元素，因为hole位置的元素已经被保存到了临时变量中了，然后再更新hole（hole = right）
3：L也是类似
4：最后二者相遇时，此相遇下标一定是坑位，将我们一开始的key（基准值）放进这个相遇的坑位中即可，此时基准值就来到了正确的位置
5：返回相遇位置hole，这样才能分开数组，去递归基准值左右的数组
代码：
int PartSort2(int* a, int left, int right)
{
// 使用三数取中法获取基准元素的正确位置
int Mid = GetMidi(a, left, right);
// 将基准元素交换到数组的最左边
Swap(&a[left], &a[Mid]);
// 把基准值保存到临时变量key中
int key = a[left];
// 将基准值的下标保存到临时变量hole（坑位）中
int hole = left;
// 当left小于right时，进行单趟排序
while (left < right)
{
// 从右向左扫描，找到第一个小于基准元素的值
while (left < right && a[right] >= key)
{
--right;
}
// 将找到的元素放到"坑"中
a[hole] = a[right];
// 更新"坑"的位置
hole = right;
// 从左向右扫描，找到第一个大于基准元素的值
while (left < right && a[left] <= key)
{
++left;
}
// 将找到的元素放到"坑"中
a[hole] = a[left];
// 更新"坑"的位置
hole = left;
}
// 最后，将基准元素放到正确的位置（hole此时指向的位置）
a[hole] = key;
// 返回基准元素的最终位置
return hole;
}3：前后指针法
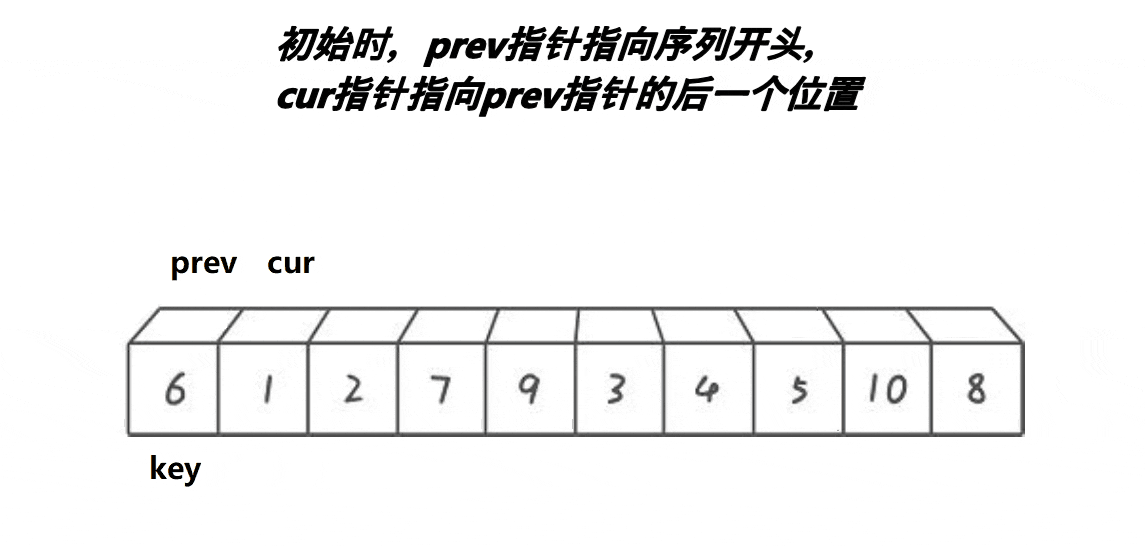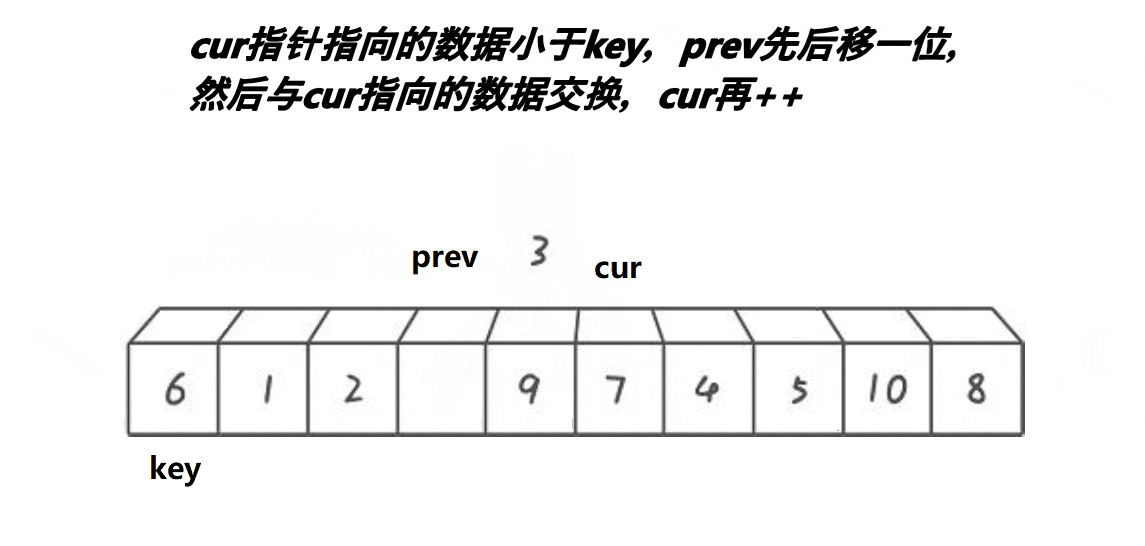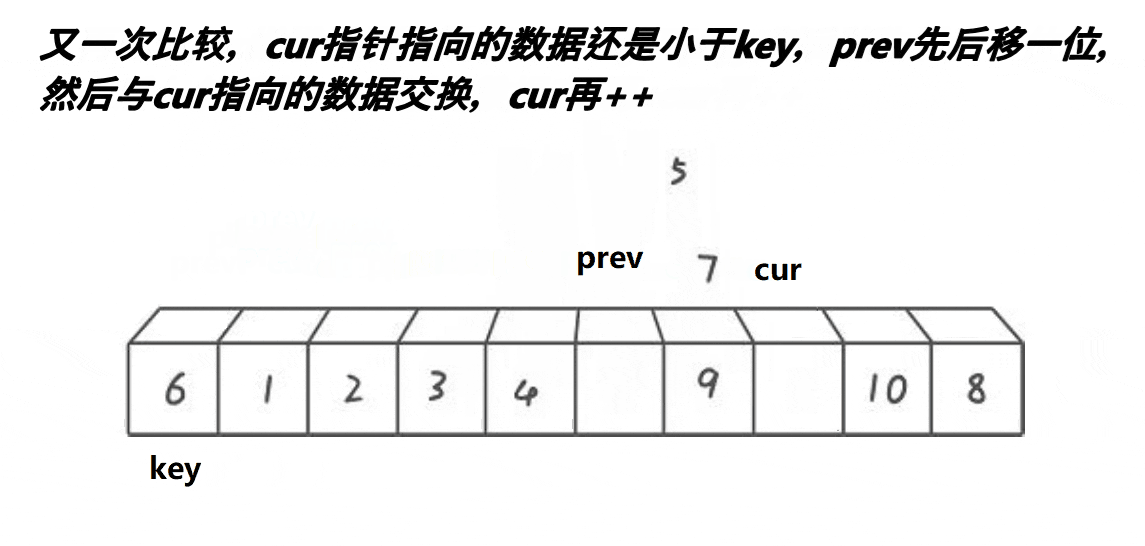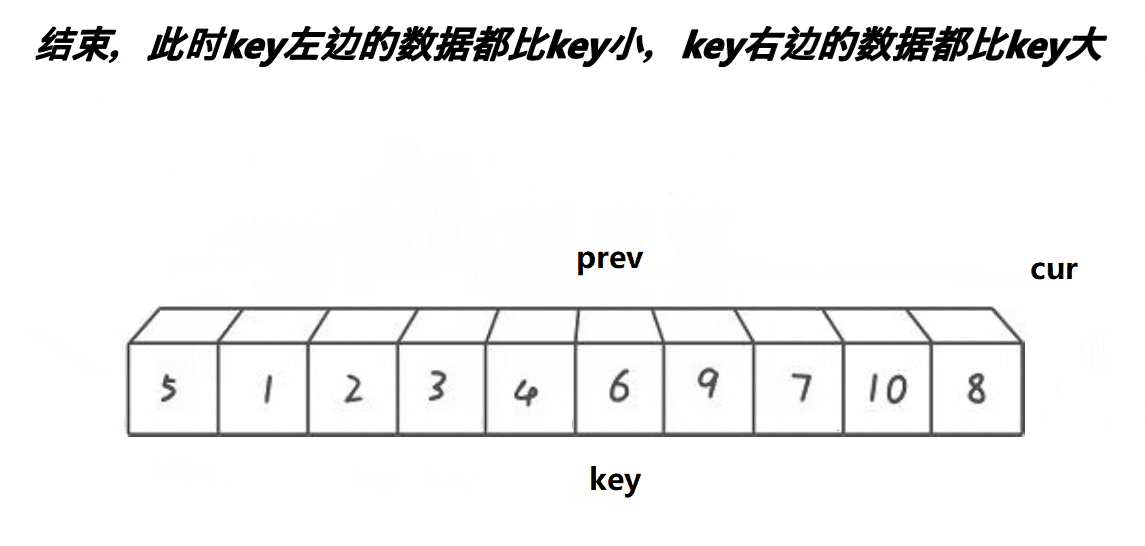
解释：
1：cur不断地找小于基准值的值，将其不断地丢到左面去
2：prev和cur的间隔有两种情况：
第一种：在cur还没有遇到比key大的值的时候，prev紧跟着cur
第二种：在cur遇到了比key大的值的时候，prefv和cur之间隔着一个或多个比key大的值
3：本质就是把一段大于key的区间，通过prev和cur交换的方法，推到右面去，同时小的也甩到 了左面去
4：如图所示:
可以看出来，一段比key（6）大的区间（7 8 9 10）都逐渐的被推到了右面，同时原先处于右面的比key（6）小的值 （3 4 5）被甩到了左面，然后再把最左面的基准值放进prev中即可，此时6来到了正确的位置。
代码：
//前后指针法实现
int PartSort3(int* a, int left, int right)
{
// 1. 获取基准值
int midi = GetMidi(a, left, right);
// 将基准元素交换到数组的最左边
Swap(&a[left], &a[midi]);
// 2. 初始化指针
int prev = left; // 设置前指针prev为起始位置
int cur = prev + 1; // 设置后指针cur为起始位置的后一个元素
// 3. 单趟排序
//cur<=right，代表还有元素需要比较
while (cur <= right)
{
// 4. 比较和交换
if (a[cur] < a[keyi] && ++prev != cur) //如果后指针cur所指向的元素小于基准值，
//并且prev+1不等于cur才会进行交换
//那么就将prev的后一个（prev+1）和cur进行交换
{
//交换
Swap(&a[prev], &a[cur]);
}
// 5. 移动指针
++cur; // 继续移动后指针cur
}
// 6. 交换基准值
Swap(&a[prev], &a[keyi]);
// 7. 返回基准值位置
return prev;
}代码解释：
对于这一步 ：if (a[cur] < a[keyi] && ++prev != cur) 进入交换的判断条件的解释：
1：左面是a[cur] < a[keyi] ，代表cur找到了比key小的值满足&&的左面
2：右面是 ++prev != cur ，这是一个前置++，代表prev+1 不等于 cur，也就是说，prev的下一个不是cur满足&&的右面，需要注意的是，这不仅是判断的时候的++，在进行交换的时候，prev也已经++了
3：为什么满足以上两点才能进入交换？
因为即使cur找到了比key小的值，但是此时prev就在他的前面，交换也没有意义，Swap(&a[prev], &a[cur]); 这一步只会让cur自己交换，所以我们得让二者之间有一定的间隔，此时prev在经过了循环的判断条件中的前置++之后，指向一段比key大的区间的第一个值，然后再与cur交换才有意义。
如图所示：
四：递归实现快速排序
1：普通递归
Hoare的递归快排：
//递归快排(霍尔)
void QuickSort1(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort1(a, left, right);
QuickSort1(a, left, keyi - 1);
QuickSort1(a, keyi + 1, right);
}挖坑法的递归快排：
//递归快排（挖坑）
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort2(a, left, right);
QuickSort2(a, left, keyi - 1);
QuickSort2(a, keyi + 1, right);
}前后指针的递归快排：
//递归快排（前后指针）
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort3(a, left, right);
QuickSort3(a, left, keyi - 1);
QuickSort3(a, keyi + 1, right);
}总结：
递归的去执行单趟，最后得到有序的数组，排序函数把key位置确定了，返回了key的下标keyi，所以左数组是left~keyi-1，右数组是keyi+1~right。
2：优化递归
意义：
我们知道：一个二叉树的最后三层，占据了总结点的%87.5
所以优化递归的思路：当接收到的数组<= 10个的时候，我们不再递归，（10个开始递归到结束就是最后的3层）而是采取插入排序来进行排序，插入不懂请看：插入排序-CSDN博客
代码：
void BetterQuickSort(int* a, int left, int right)
{
// 如果left大于或等于right，则数组为空或只有一个元素，无需排序，直接返回
if (left >= right)
return;
// 如果数组长度大于10，则使用PartSort1进行快速排序
if ((right - left + 1) > 10)
{
// 调用PartSort1函数获取基准值的位置
int keyi = PartSort1(a, left, right);
// 对基准值左边的部分进行快速排序
QuickSort1(a, left, keyi - 1);
// 对基准值右边的部分进行快速排序
QuickSort1(a, keyi + 1, right);
}
// 如果数组长度小于或等于10，则使用插入排序
else
{
// 对left到right之间的部分进行插入排序
InsertSort(a + left, right - left + 1);
}
}五：非递归实现快速排序
以上的所有快速排序都是递归快排，也可以借助栈来实现非递归的快排
void QuickSortNoneR(int* a, int left, int right)
{
// 1. 初始化栈
ST st;
STInit(&st);
// 2. 入栈：将right和left的值分别入栈
STPush(&st, right);
STPush(&st, left);
// 3. 栈不为空时继续处理
while (!STEmpty(&st))
{
// 4. 出栈：从栈顶取出begin和end的值
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
// 5. 调用PartSort1函数获取基准值的位置
int keyi = PartSort1(a, begin, end);
// 6. 入栈：根据keyi的位置，将右半部分和左半部分的起始位置入栈
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (keyi - 1 > begin)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
// 7. 销毁栈
STDestroy(&st);
}解释：
1 ：栈是后进先出，所以我们入栈和出栈的时候，都要格外的注意
2：我们先入right，再入left，这样就能先取到left，再取到right，然后进行单趟的排序函数
3：然后通过单趟的排序函数返回的key1（基准值来到正确位置后的下标），来进行左右数组的划分
3：因为我们递归是先取排序左数组，再去排序右数组，所以我们先入栈右数组的，再入栈左数组，这样下一次出栈的时候，就是先得到左数组的，再得到右数组
4：销毁栈
总结：就是用栈的性质，不断去出栈入栈，结合单趟的排序函数来实现快排。
六：运行测试
1：十万数据数组
2：百万数据数组
3：千万数据数组
时间的单位是ms
七：代码分享
1：Stack.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->capacity = 0;
ps->top = 0;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newCapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
void STPop(ST* ps)
{
assert(ps);
//
assert(ps->top > 0);
--ps->top;
}
STDataType STTop(ST* ps)
{
assert(ps);
//
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}2:Stack.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//#define N 10
//struct Stack
//{
// int a[N];
// int top;
//};
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
void STInit(ST* ps);
void STDestroy(ST* ps);
void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
STDataType STTop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
3：快排的所有实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include "Stack.h"
//插入函数
void InsertSort(int* arr, int N)
{
for (int i = 0; i < N - 1; i++)
{
int end = i;
//即将排序的元素，保留在tmp
int tmp = arr[end + 1];
//end>=0代表还有元素未比较
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
//来到这里分为两种情况
//1：break->遇到比元素tmp小或和tmp相等的，将m放在它的后面
//2：全部比较完了，都没有遇到<=tmp的，最后tmp放在数组第一个位置
arr[end + 1] = tmp;
}
}
//交换
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//三数取中
int GetMidi(int* a, int left, int right)
{
// 计算中间元素的下标
int mid = (left + right) / 2;
// 比较三个元素：left, mid, right
// 首先比较left和mid
if (a[left] < a[mid])
{
// 如果left < mid，再比较mid和right
if (a[mid] < a[right])
{
// 如果left < mid < right，则mid是中间值
return mid;
}
else if (a[left] > a[right]) // 如果left > right，则mid是最大值
{
// 在这种情况下，left是中间值
return left;
}
else
{
// 如果left < right，则right是中间值
return right;
}
}
else // 如果a[left] > a[mid]
{
// 比较mid和right
if (a[mid] > a[right])
{
// 如果mid > right，则mid是中间值
return mid;
}
else if (a[left] < a[right]) // 如果left < right，则mid是最小值
{
// 在这种情况下，left是中间值
return left;
}
else
{
// 如果left > right，则right是中间值
return right;
}
}
}
//全部忘加[],第二个写成if
//第一种单趟：霍尔法
int PartSort1(int* a, int left, int right)
{
// 使用三数取中法获取基准元素的正确位置
int Mid = GetMidi(a, left, right);
// 将基准元素交换到数组的最左边
Swap(&a[left], &a[Mid]);
// 设置基准元素的索引为keyi
int keyi = left;
// 当left小于right时，进行单趟排序
while (left < right)
{
// 从右向左扫描，找到第一个小于基准元素的值
while (left < right && a[right] >= a[keyi])
{
right--;
}
// 注意，这里使用&&连接两个条件，并且顺序很重要，
// 因为如果left >= right，我们就不再需要继续比较
// 此时a[right] >= a[keyi]放在前面的话，会越界访问
// 从左向右扫描，找到第一个大于基准元素的值
while (left < right && a[left] <= a[keyi])
{
left++;
}
// 交换两个元素，将大于基准的元素放到右边，小于基准的元素放到左边
Swap(&a[left], &a[right]);
}
// 最后，将基准元素放到正确的位置（left此时指向的位置）
Swap(&a[keyi], &a[left]);
// 返回基准元素的最终位置
return left;
}
//挖坑法
int PartSort2(int* a, int left, int right)
{
// 使用三数取中法获取基准元素的正确位置
int Mid = GetMidi(a, left, right);
// 将基准元素交换到数组的最左边
Swap(&a[left], &a[Mid]);
// 设置基准元素的值
int key = a[left];
// 设置基准元素的位置
int hole = left;
// 当left小于right时，进行单趟排序
while (left < right)
{
// 从右向左扫描，找到第一个小于基准元素的值
while (left < right && a[right] >= key)
{
--right;
}
// 将找到的元素放到"坑"中
a[hole] = a[right];
// 更新"坑"的位置
hole = right;
// 从左向右扫描，找到第一个大于基准元素的值
while (left < right && a[left] <= key)
{
++left;
}
// 将找到的元素放到"坑"中
a[hole] = a[left];
// 更新"坑"的位置
hole = left;
}
// 最后，将基准元素放到正确的位置（hole此时指向的位置）
a[hole] = key;
// 返回基准元素的最终位置
return hole;
}
前后指针法
//int partsort3(int* a, int left, int right)
//{
// int prev = left;
// int cur = left + 1;
//
// while (cur <= right)
// {
// if (a[cur] < a[left] && ++prev != cur)
// {
// Swap(&a[cur], &a[prev]);
//
// }
// cur++;
// }
// Swap(&a[prev], &a[left]);
// //最后比left元素小的 都集中在了prev的下面及其左面，此时prev和left交换，最左面的元素一定是来到了正确的位置
// return prev;
// //a[cur] < a[left] 后 cur肯定是要++的，
// //如果此时prev+1 = cur就代表prev和cur之间还没有比下标为left的元素大的元素，所以没必要交换，
// //当++prev!=cur 的时候才交换，其次++prev!=cur 不仅判断还+1了，
//}
//第三种单趟：前后指针法
//int partsort3(int* a, int left, int right)
//{
// int Mid = GetMidi(a, left, right);
// Swap(&a[left], &a[Mid]);
//
// int prev = left;
// int cur = prev + 1;
// int keyi = left;
//
// while (cur <= right)
// {
// if (a[cur] < a[keyi] && ++prev != cur)
// {
// Swap(&a[cur], &a[prev]);
//
// }
// cur++;
// }
// Swap(&a[prev], &a[keyi]);
// return prev;
//}
//前后指针法
int PartSort3(int* a, int left, int right)
{
// 1. 获取基准值
int midi = GetMidi(a, left, right);
// 将基准值与数组的第一个元素交换，确保基准值位于起始位置
Swap(&a[left], &a[midi]);
// 2. 初始化指针
int prev = left; // 设置前指针prev为起始位置
int cur = prev + 1; // 设置后指针cur为起始位置的后一个元素
int keyi = left;
// 3. 单趟排序
while (cur <= right)
{
// 4. 比较和交换
if (a[cur] < a[keyi] && ++prev != cur) // 如果后指针cur所指向的元素小于基准值
{
Swap(&a[prev], &a[cur]); // 并且前指针prev还没有到达cur的位置，
// 则将前指针向前移动一位，并与后指针指向的元素交换
}
// 5. 移动指针
++cur; // 继续移动后指针cur
}
// 6. 交换基准值
Swap(&a[prev], &a[keyi]);
// 7. 返回基准值位置
return prev;
}
// 交换两个元素
void Swap(int* x, int* y)
{
int temp = *x;
*x = *y;
*y = temp;
}
//递归快排(霍尔)
void QuickSort1(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort1(a, left, right);
QuickSort1(a, left, keyi - 1);
QuickSort1(a, keyi + 1, right);
}
//递归快排（挖坑）
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort2(a, left, right);
QuickSort2(a, left, keyi - 1);
QuickSort2(a, keyi + 1, right);
}
//递归快排（前后指针）
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = PartSort3(a, left, right);
QuickSort3(a, left, keyi - 1);
QuickSort3(a, keyi + 1, right);
}
//优化递归快排
void BetterQuickSort(int* a, int left, int right)
{
if (left >= right)
return;
if ((right - left + 1) > 10)
{
int keyi = PartSort1(a, left, right);
QuickSort1(a, left, keyi - 1);
QuickSort1(a, keyi + 1, right);
}
else
{
InsertSort(a + left, right - left + 1);
}
//左面确认起点，右面确认个数
}
//非递归快排，借助栈
void QuickSortNoneR(int* a, int left, int right)
{
// 1. 初始化栈
ST st;
STInit(&st);
// 2. 入栈：将right和left的值分别入栈
STPush(&st, right);
STPush(&st, left);
// 3. 栈不为空时继续处理
while (!STEmpty(&st))
{
// 4. 出栈：从栈顶取出begin和end的值
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
// 5. 调用PartSort1函数获取基准值的位置
int keyi = PartSort1(a, begin, end);
// 6. 入栈：根据keyi的位置，将右半部分和左半部分的起始位置入栈
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (keyi - 1 > begin)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
// 7. 销毁栈
STDestroy(&st);
}
//非递归快排(借助栈)
//void QuickSortNoneR(int* a, int begin, int end)
//{
// ST st;
// STInit(&st);
// STPush(&st, end);
// STPush(&st, begin);
// while (!STEmpty(&st))
// {
// int left = STTop(&st);
// STPop(&st);
//
// int right = STTop(&st);
// STPop(&st);
//
// int keyi = PartSort1(a, left, right);
// // [lefy,keyi-1] keyi [keyi+1, right]
// if (keyi + 1 < right)
// {
// STPush(&st, right);
// STPush(&st, keyi + 1);
// }
//
// if (left < keyi - 1)
// {
// STPush(&st, keyi - 1);
// STPush(&st, left);
// }
// }
//
// STDestroy(&st);
//}
//测试少量快排
void Test1()
{
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
QuickSortNoneR(a, 0, sizeof(a) / sizeof(int) - 1);
PrintArray(a, sizeof(a) / sizeof(int));
}
//测试大量快排
void Test2()
{
srand(time(0));
int N = 10000000;
int* a1 = (int*)malloc(sizeof(int) * N);
for (int i = N - 1; i >= 0; --i)
{
a1[i] = rand() + i;
}
int begin1 = clock();
QuickSort1(a1, 0, N - 1);
int end1 = clock();
printf("QuickSort1:%d\n", end1 - begin1);
free(a1);
}
//测试优化递归后的大量快排
void Test3()
{
srand(time(0));
int N = 10000000;
int* a1 = (int*)malloc(sizeof(int) * N);
for (int i = N - 1; i >= 0; --i)
{
a1[i] = rand() + i;
}
int begin1 = clock();
BetterQuickSort(a1, 0, N - 1);
int end1 = clock();
printf("BetterQuickSort:%d\n", end1 - begin1);
free(a1);
}
//测试非递归快排
void Test4()
{
srand(time(0));
int N = 10000000;
int* a1 = (int*)malloc(sizeof(int) * N);
for (int i = N - 1; i >= 0; --i)
{
a1[i] = rand() + i;
}
int begin1 = clock();
QuickSortNoneR(a1, 0, N - 1);
int end1 = clock();
printf("QuickSortNoneR:%d\n", end1 - begin1);
free(a1);
}
int main()
{
//测试递归少量快排
Test1();
//测试递归大量快排
Test2();
//测试优化递归大量快排
Test3();
//测试非递归大量快排
Test4();
return 0;
}
谢谢观看~~~~