MATLAB|基于多时段动态电价的电动汽车有序充电策略优化
目录
主要内容
模型研究
一、蒙特卡洛模拟
部分代码
部分结果一览
下载链接
主要内容
该模型参考文献《基于多时段动态电价的电动汽车有序充电策略优化》,采用蒙特卡洛随机抽样方法来模拟电动汽车无序充电状态下的负荷曲线,并设置三个对比算例--基础场景(无电动汽车)、电动汽车无序充电和电动汽车有序充电场景,有序充电场景以电网端负荷差最小和用户侧充电成本最经济为目标,通过粒子群算法进行求解,程序采用matlab+matpower计算,注释清楚,运行稳定,出图效果好!

模型研究
一、蒙特卡洛模拟
蒙特卡洛模拟是对事件中的变量做统计分析,拟合出概率分布函数,通过抽样生成满足该分布的近似数据,然后对这些近似数据采取进一步分析,做出判断。因此,在电动汽车充电分析中,综合一定规模电动汽车充电特征,能够得出电动汽车群体的充电特点,具体蒙特卡洛求解电动汽车充电特征的流程图如下:
部分代码
% 计算各节点电动汽车充电需求
P_L_EV = zeros(33,24);
for i=1:33
P_L_EV(i,:) = sum(Load_EV((i-1)*car_number/33+1:(i-1)*car_number/33+car_number/33,:))/1000;
end
% 计算实际的总体负荷
mpc=case33bw;
P_L_act = sum(Power_load.*mpc.bus(:,3))+sum(P_L_EV);
% 验证是否满足潮流约束并计算最优潮流
V = zeros(33,24);% 逐时记录电压
P_loss = zeros(1,24);% 逐时记录网损
for t=1:T
mpc=case33bw;
mpc.bus(:,3)=Power_load(t).*mpc.bus(:,3);% 当前时刻各节点基础负荷
mpc.bus(:,3)=mpc.bus(:,3)+P_L_EV(:,t);% 加上电动汽车充电渡河
[result,sucess]=runopf(mpc,mpoption('OUT_ALL',0,'VERBOSE',0,'PF_ALG',3));% matpower计算最优潮流
V(:,t) = result.bus(:,8);% 当前时刻各节点电压幅值
P_loss(t) = sum(result.branch(:,14)+result.branch(:,16));% 当前时刻系统网损
if sucess == 1% 判断是否满足潮流约束
% disp('当前场景满足潮流约束!')
elseif sucess == 0
disp('当前场景不满足潮流约束!')
end
end
%% 优化结果可视化
[fun,C_1,C_2] = objective2(bestPosition);
C_1_0 = sqrt((sum((P_L_base*1000-mean(P_L_base)*1000).^2))/24);
C_2_1 = sum(sum(P_EV_0).*csell);
disp('%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
')
disp('
%% 场景3结果输出 %
%
')
disp('
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%
')
disp(['
总目标函数的值为 :
',num2str(fun)])
disp(['
基础负荷波动的标准差为 :
',num2str(C_1_0)])
disp(['
总体负荷波动的标准差为 :
',num2str(C_1)])
disp(['
考虑动态电价电车用户的充电费用为:
',num2str(C_2)])
disp(['
不考虑动态电价电车用户的充电费用为:
',num2str(C_2_1)])
disp(['
总体负荷曲线的峰值为 :
',num2str(max(P_L_act*1000))])
disp(['
总体负荷曲线的谷值为 :
',num2str(min(P_L_act*1000))])
disp('
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%
')
部分结果一览
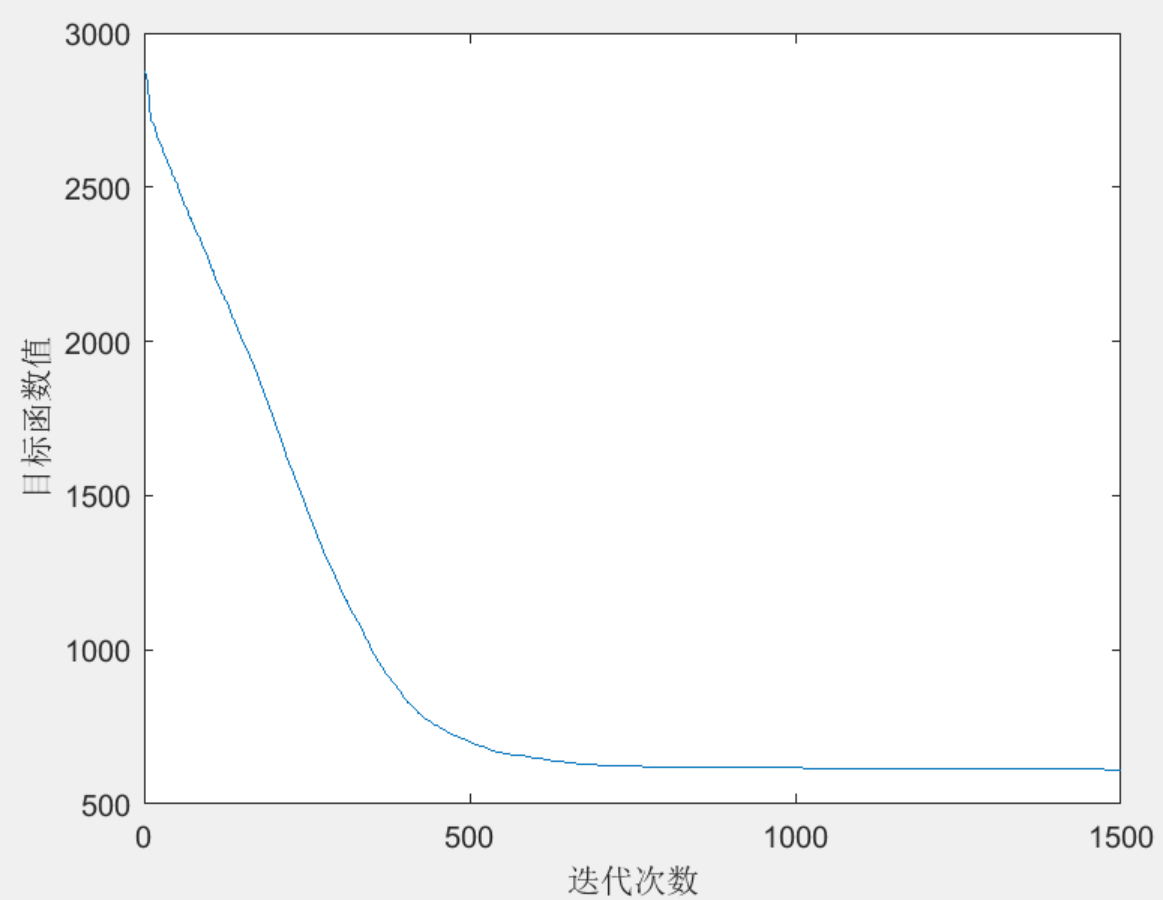
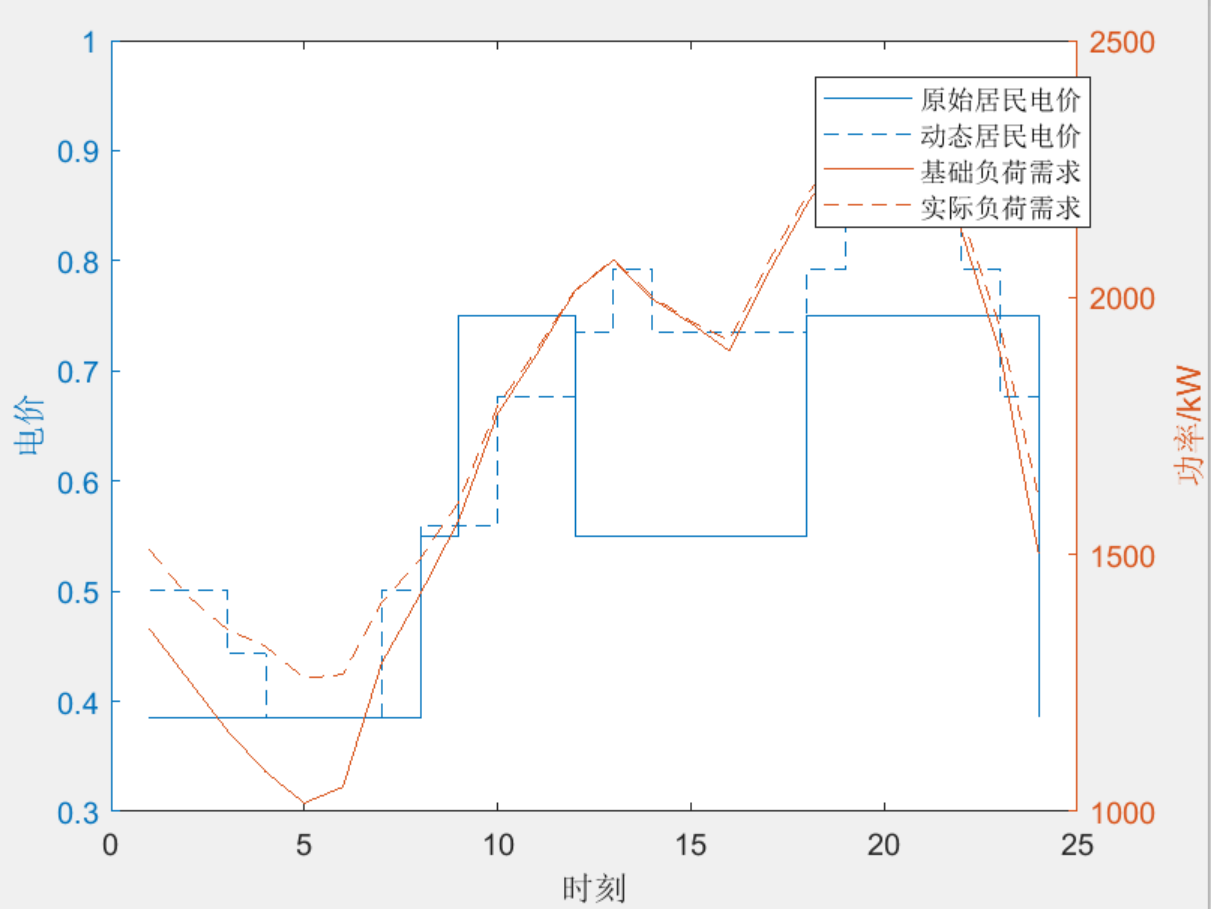
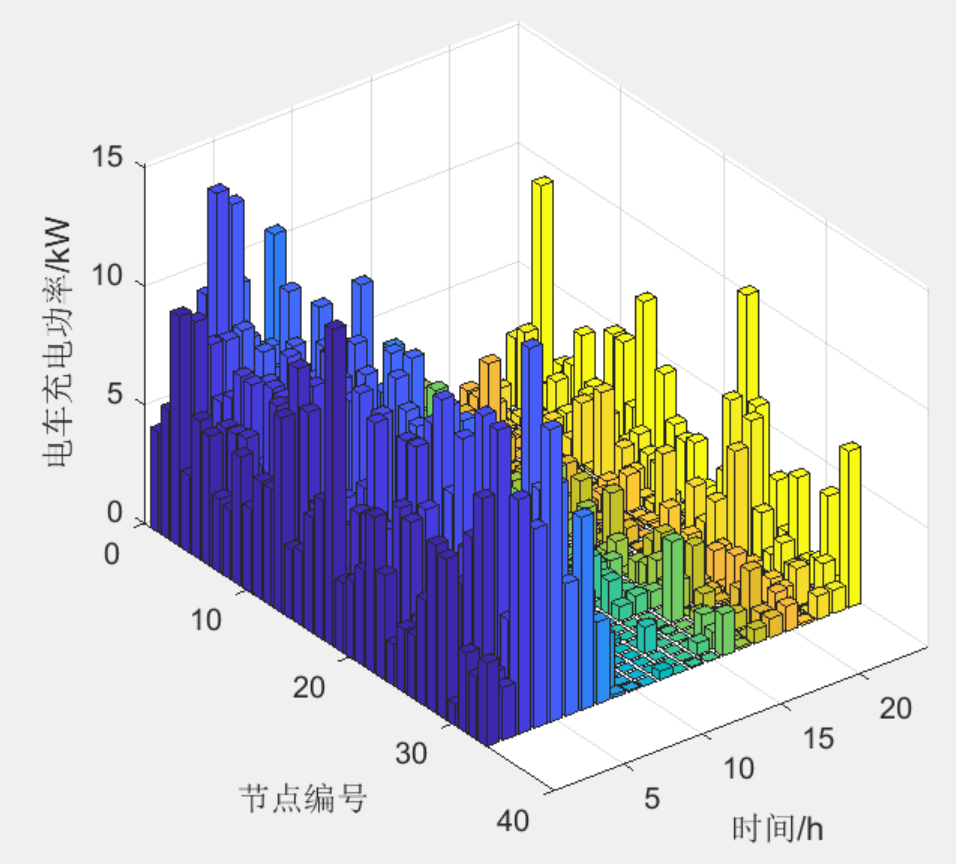
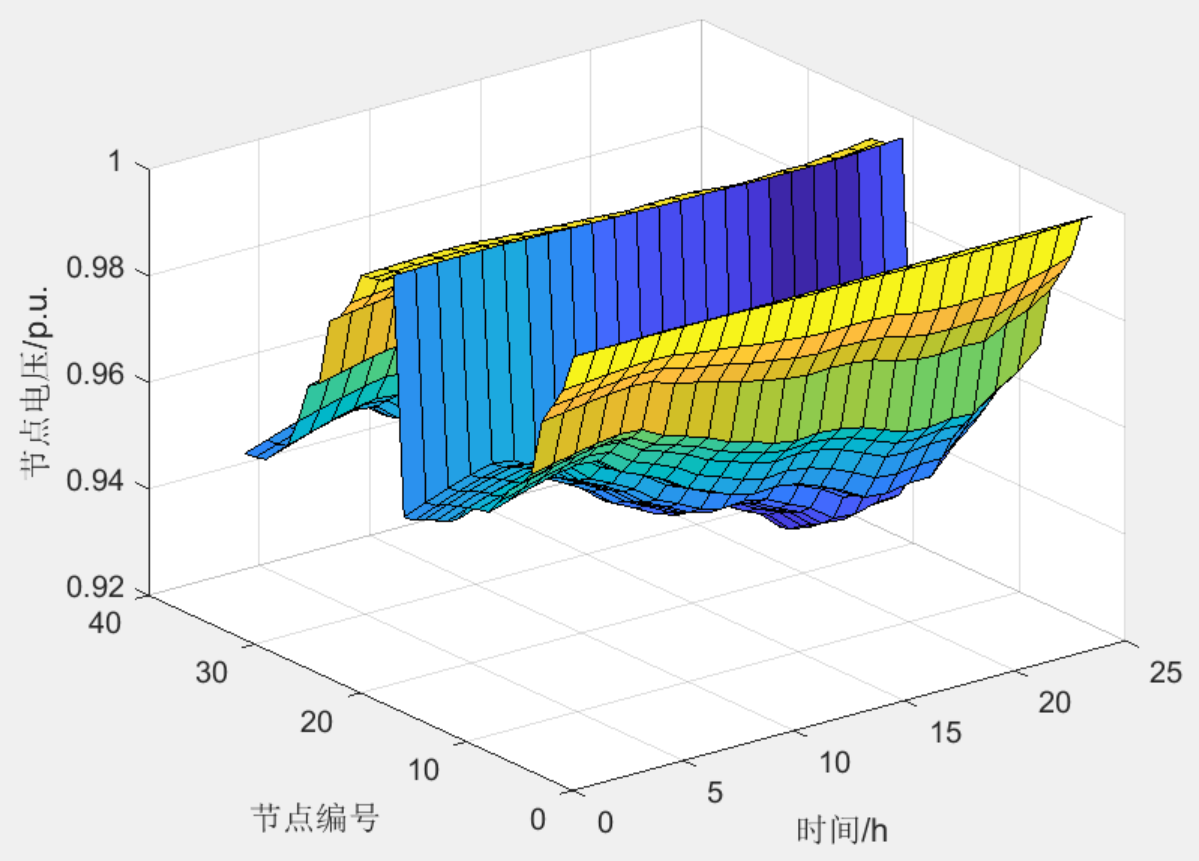
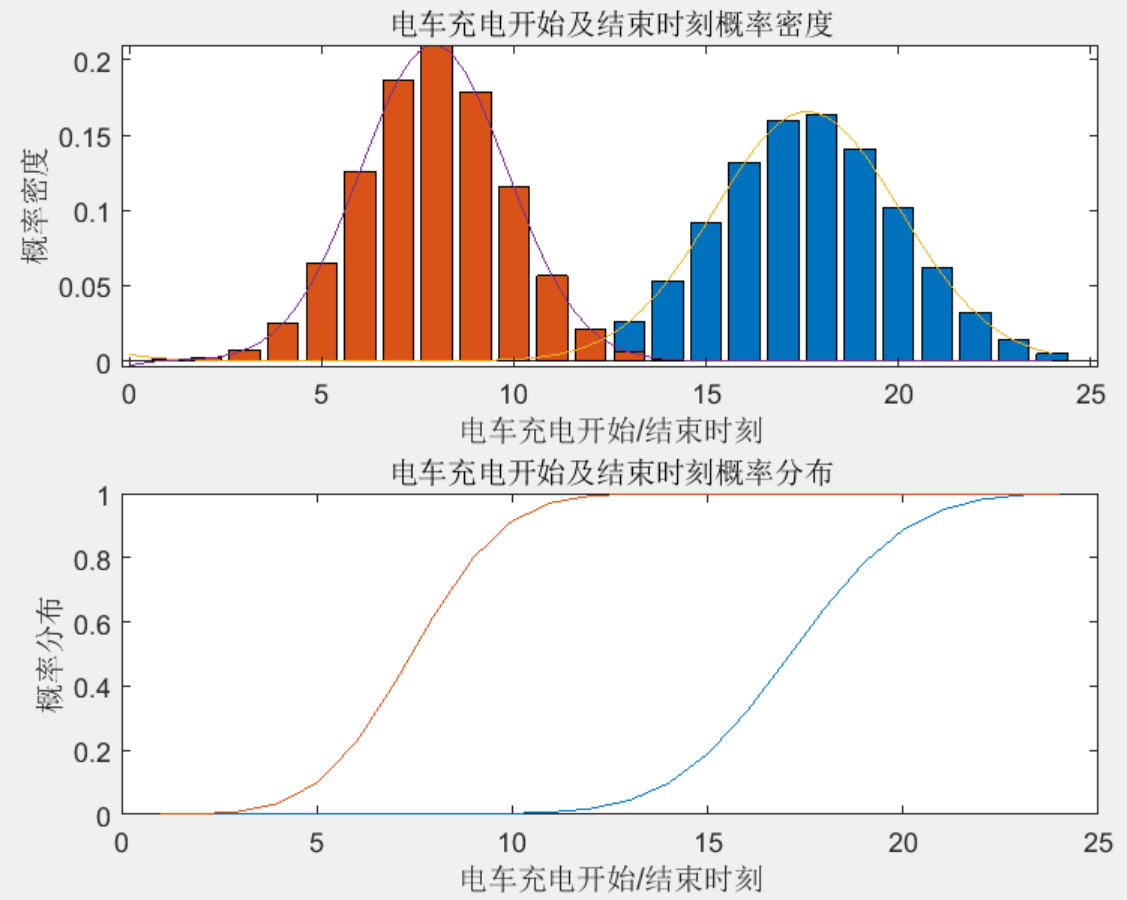
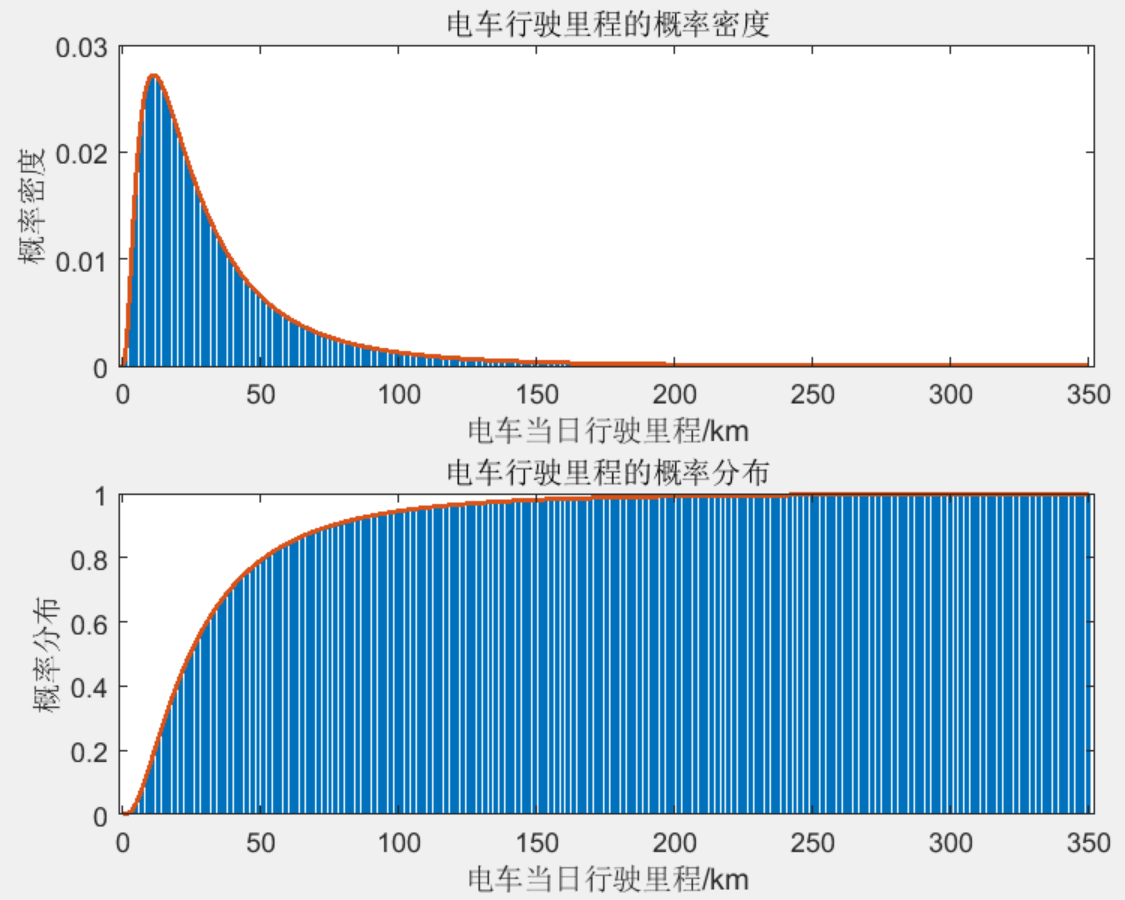
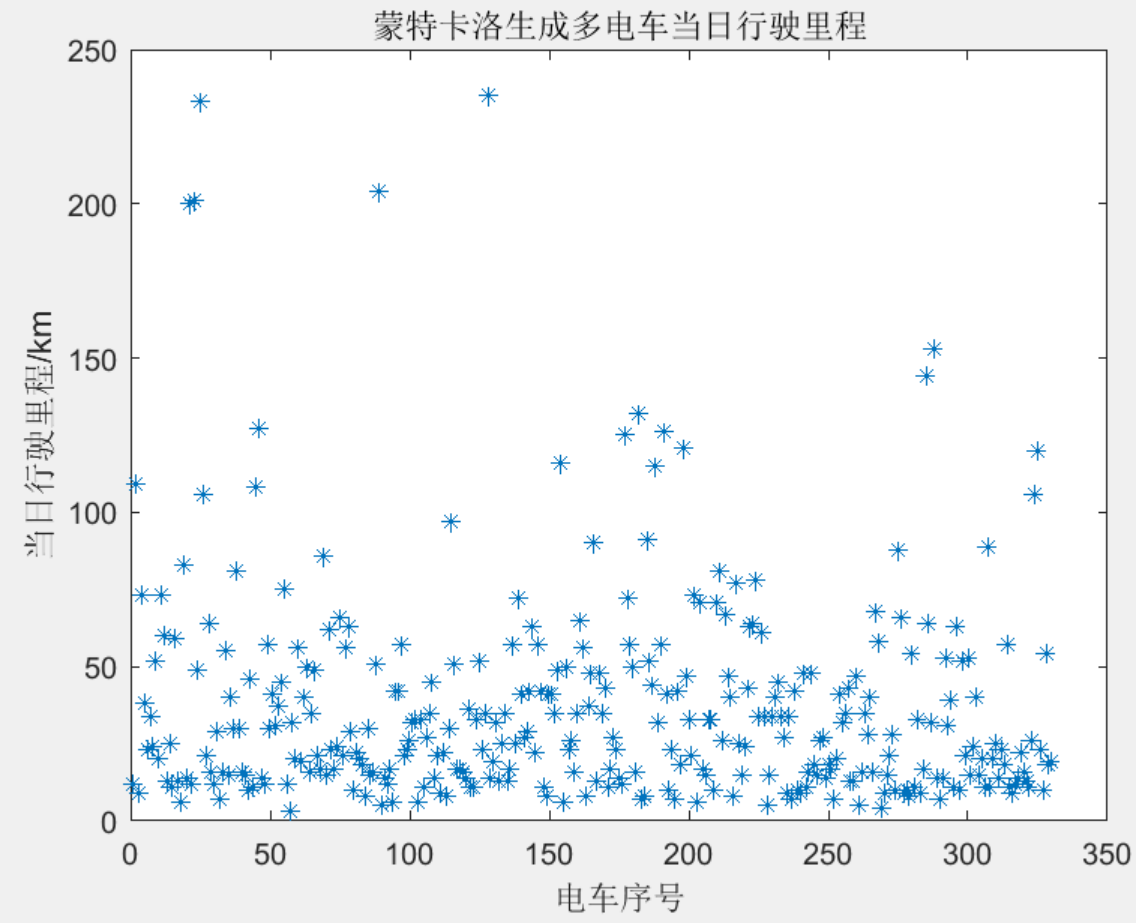
下载链接
