当前位置：首页 > article >正文

数据结构和算法之树形结构(1)

article 2024/9/21 13:51:50

文章出处: 数据结构和算法之树形结构(1) 关注码农爱刷题，看更多技术文章！！

树形结构是数据结构四种逻辑结构之一，也是被广泛使用的一种逻辑结构，它描述的是数据元素之间一对多的逻辑关系。树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合；它有一个起始节点，称之为根节点；从根节点往下逐层延伸，每个节点都可以有零个或多个子节点，有且只有一个父节点，根节点无父节点，形体像一棵倒挂的树，因而被称之为树形结构。树形结构逻辑上有序的意思，就是从根节点往下延伸的顺序，因而和线性结构一样是有序结构。

树形结构常用于表示具有层次关系的数据，例如文件系统、组织结构、目录结构等。它提供了一种便捷的方式来组织和访问数据。树形结构的应用非常广泛，例如在计算机科学中，树型结构被用于实现搜索算法（如二叉搜索树）、存储和检索数据（如B树、堆）、表达抽象语法树等。在现实生活中，树型结构也有很多应用，比如家谱、图书分类、产品组织关系等。

一、基本概念

二、二叉树

二叉树的定义

二叉树是典型和常见的树形结构，也是最简单的树形结构。二叉树每个节点最多有两棵子树（二叉树中不存在度大于2的节点），并且二叉树的子树有左右之分，顺序不能颠倒。

二叉树根据样式不同，还可以分为满二叉树和完全二叉树，例如下图：

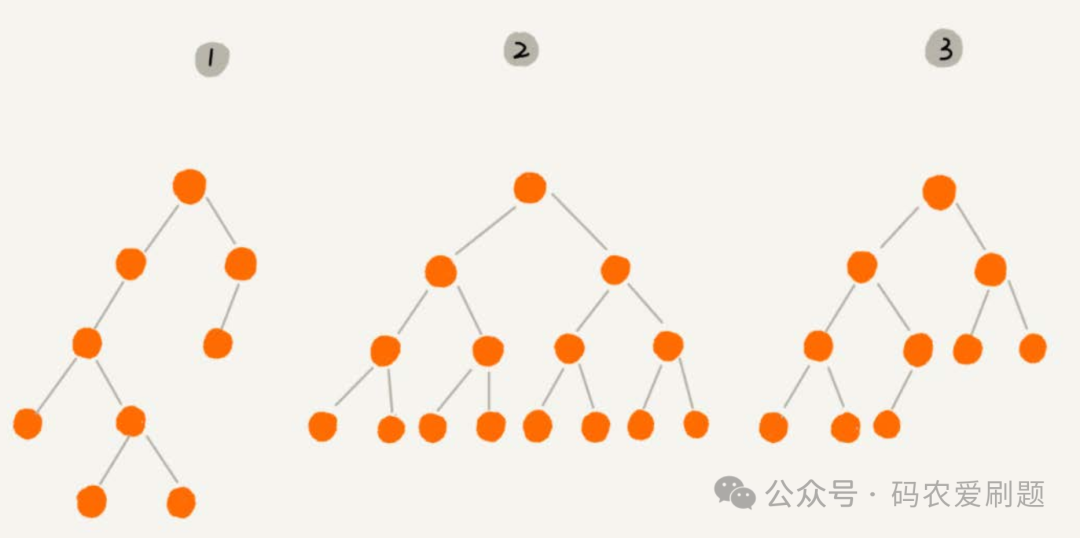
若一棵树的层数为k，它总结点数是2^k-1，则这棵树就是满二叉树。上图编号2的树就是一棵满二叉树，该树4层节点数15 = 2^4-1；满二叉树的特点是叶子节点都在最底层，除了叶子节点，每个节点都有左右两个子节点。

若一棵树的层数为k，它前k-1层的总结点数是2^(k-1)-1，第k层的结点按照从左往右的顺序排列，则这棵树就是完全二叉树。上图编号3的树就是一棵完全二叉树，该树4层前3层节点数7 = 2^(4-1)-1；完全二叉树的特点是：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大值2。看下图识别完全二叉树和非完全二叉树的区别。

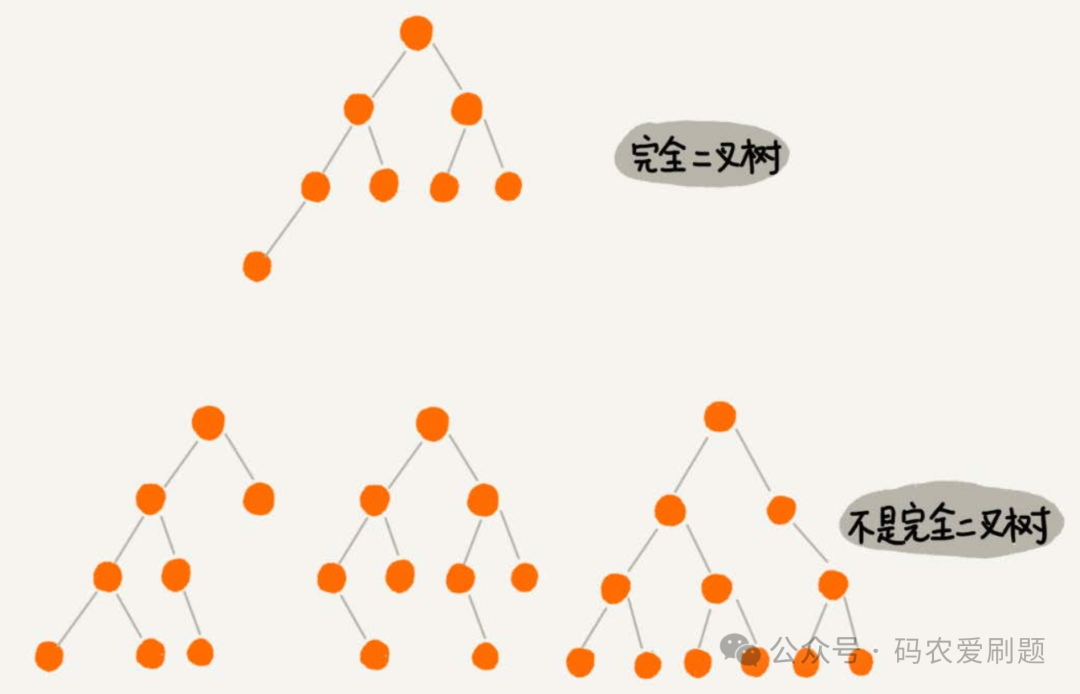
此外，满二叉树一定是一棵完全二叉树，但完全二叉树不一定是满二叉树。

二叉树的存储结构

二叉树在实际落地时，可以采用顺序存储结构和链式存储结构，关于两者的区别可以参看前面的文章数据结构和算法之基本概念。如果是采用链式存储结构，一个节点分为三部分，其中数据域存储数据，另外两个指针域，一个指向左边的子节点，一个指向右边的子节点，这是一个典型的链表结构(关于链表结构说明可以参看文章数据结构和算法之线性结构)。通常，这是二叉树常用的存储结构。

如果采用顺序存储结构，通常是采用数组来实现。那数组是如何存储二叉树节点数据的呢? 其存储规则是：从根节点开始，逐层往下、从左至右依次存储，看下图能更形象地理解其存储规则：

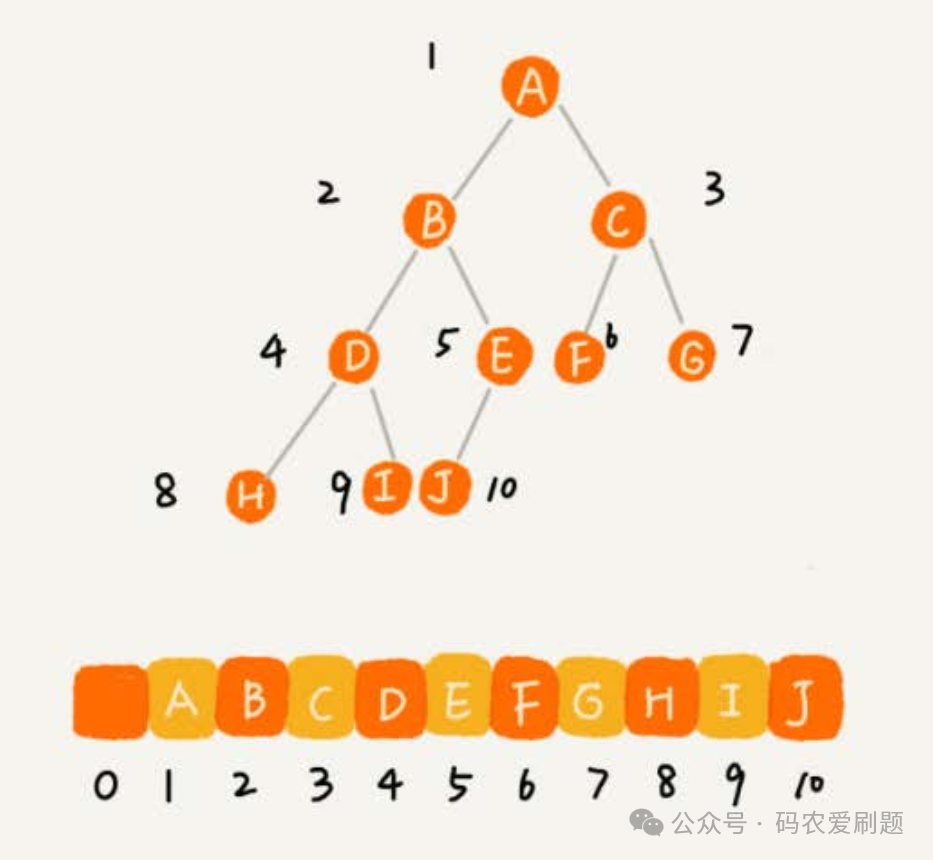
从上图可以看出：如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点；反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为1的位置），这样就可以通过下标计算，把整棵树都串起来。

二叉树的遍历

二叉树的遍历通常有两种搜索遍历方法：深度优先遍历与广度优先遍历。深度优先遍历（Depth-First Search，简称DFS)即优先深入地探索一个节点的某一条路径，直到该路径都已被探索完，然后再回溯到该节点，探索该节点另一条路径，以此类推；广度优先遍历（Breadth-First Search，简称BFS）则是同时对所有路径逐层进行探索。

深度优先遍历根据遍历的顺序不同，又可以细分为三种不同的遍历顺序：前序遍历、中序遍历、后序遍历。三种遍历顺序定义如下：

无论哪种遍历顺序，左节点都要优先右节点遍历，三种遍历顺序实际遍历结果以下图为例：

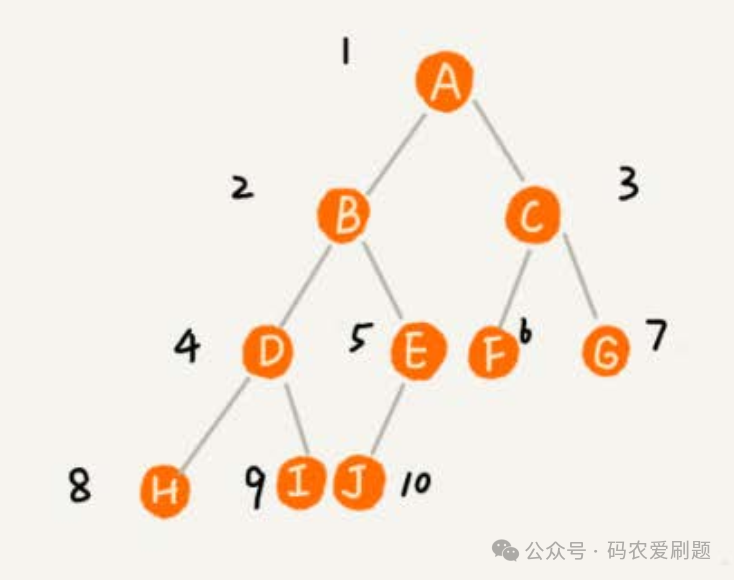
前序遍历结果是：ABDHIEJCFG; 中序遍历结果是：HDIBJEAFCG;后序遍历结果是：HIDJEBFGCA。代码层面，通常我们可以通过递归实现前述深度优先遍历的三种遍历顺序，代码如下：

public class Solution { 
    private static class Node { 
        public int data;  // 节点值
        public Node left;  // 左节点  
        public Node right;  // 右节点
 
        public Node(int data, Node left, Node right) { 
            this.data = data; 
            this.left = left; 
            this.right = right; 
        } 
    } 
 
    public static void preDfs(Node treeNode) { 
        if (treeNode == null) { 
            return; 
        } 
        System.out.println(treeNode.data);  // 访问节点本身
        preDfs(treeNode.left);  // 遍历左节点
        preDfs(treeNode.right);  // 遍历右节点
    } 
    
    public static void middleDfs(Node treeNode) { 
        if (treeNode == null) { 
            return; 
        }        
        middleDfs(treeNode.left);  // 遍历左节点
        System.out.println(treeNode.data);  // 访问节点本身
        middleDfs(treeNode.right);  // 遍历右节点
    } 
    
     public static void lastDfs(Node treeNode) { 
        if (treeNode == null) { 
            return; 
        }        
        lastDfs(treeNode.left);  // 遍历左节点      
        lastDfs(treeNode.right);  // 遍历右节点
        System.out.println(treeNode.data);  // 访问节点本身
    } 
}

如果是广度优先遍历，上面二叉树图遍历的结果则是：ABCDEFGHIJ；广度优先遍历符合队列先进先出的特点，实现时可以考虑用队列，如下面代码：


public static void bfs(Node root) {
    if (root == null) {
        return;
    }

    LinkedList<Node> queue = new LinkedList<Node>();
    Node current = null;
    // 根节点入队
    queue.offer(root);

    // 左侧数的深度
    int leftNum = 0;
    // 右侧数的深度
    int rightNum = 0;

    // 只要队列中有元素，就可以一直执行，非常巧妙地利用了队列的特性
    while (!queue.isEmpty()) {
        // 出队队头元素 先进先出
        current = queue.poll();
        System.out.print("-->" + current.data);
        // 左子树不为空，入队
        if (current.left != null) {
            queue.offer(current.left);
            leftNum++;
        }

        // 右子树不为空，入队
        if (current.right != null) {
            queue.offer(current.right);
            rightNum++;
        }
    }
    System.out.println(rightNum + "\t" + leftNum);
}

上述代码中Node类的定义与之前代码里的Node类一致。代码逻辑分析：先是根节点入队，第一次循环，根节点出队(第一层)，然后是第二层左右节点入队；第二次循环，左节点出队，左节点左右两孙节点入队；第三次循环，右节出队，右节点左右两孙节点入队，至此二层节点全部出队；第四次循环，左节点左孙节点出队，其左右子节点再入队，以此类推。

深度广度优先遍历和广度优先遍历不仅仅用于二叉树的遍历，事实上，两者是两种基本且重要的图与树的遍历算法，它们的应用场景和优缺点如下图表：