【代码随想录训练营第42期 Day60打卡 - 图论Part10 - Bellman_ford算法系列运用
目录
一、Bellman_ford算法的应用
二、题目与题解
题目一:卡码网 94. 城市间货物运输 I
题目链接
题解:队列优化Bellman-Ford算法(SPFA)
题目二:卡码网 95. 城市间货物运输 II
题目链接
题解: 队列优化Bellman-Ford算法(SPFA)
题目三:卡码网 96. 城市间货物运输 III
题目链接
题解: Bellman-Ford算法
三、小结
一、Bellman_ford算法的应用
Bellman-Ford算法是一种用于解决单源最短路径问题的算法,它能够处理含有负权边的图,并且能够检测图中是否存在负权回路。
其应用一般分为以下几个方面:
1、最短路径问题:在图论中,Bellman - Ford算法是解决单源最短路径问题的有效工具。它可以找到从一个顶点到所有其他顶点的最短路径。
2、负权边:与Dijkstra算法不同,Bellman - Ford算法能够处理含有负权边的图。这意味着它可以解决那些包含负权重边的图的最短路径问题。
3、运输问题:在运输问题中,需要找到从一个供应点(源)到多个需求点(汇)的最小成本运输路径。Bellman - Ford算法可以用来解决这个问题,尤其是在存在负权边的情况下。
4、流网络问题:在流网络中,Bellman - Ford算法可以用来找到从一个节点到另一个节点的最大流。这是因为在某些流网络问题中,边的权重可以表示为流量的限制。
5、网络流问题:在网络流问题中,Bellman - Ford算法可以用来找到从一个源点到汇点的最小费用流。这涉及到在网络中传输物质或信息,并需要最小化成本。
6、动态最短路径问题:在某些情况下,图的结构可能会发生变化,例如添加或删除边。Bellman - Ford算法可以用来动态地更新最短路径信息。
7、多源最短路径问题:Bellman - Ford算法可以扩展为解决多源最短路径问题,即找到多个源点到其他所有顶点的最短路径。
8、网络路由问题:在网络路由问题中,需要找到从一个网络节点到另一个网络节点的最佳路径。Bellman - Ford算法可以用来解决包含负权边的网络路由问题。
Bellman-Ford算法的主要优点是它能够处理负权边,这是其他最短路径算法(如Dijkstra算法)所不能做到的。然而,它的主要缺点是时间复杂度较高,为O(VE),其中V是顶点数,E是边数。在实际应用中,如果图中的边数远大于顶点数,Bellman-Ford算法可能不如Dijkstra算法高效。
二、题目与题解
题目一:卡码网 94. 城市间货物运输 I
题目链接
94. 城市间货物运输 I (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v (单向图)。
输出描述
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 "unconnected"。
输入示例
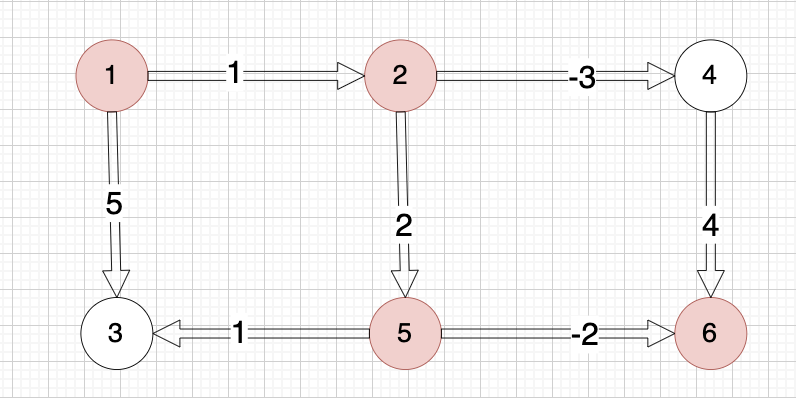
6 7 5 6 -2 1 2 1 5 3 1 2 5 2 2 4 -3 4 6 4 1 3 5输出示例
1提示信息
示例中最佳路径是从 1 -> 2 -> 5 -> 6,路上的权值分别为 1 2 -2,最终的最低运输成本为 1 + 2 + (-2) = 1。
示例 2:
4 2
1 2 -1
3 4 -1在此示例中,无法找到一条路径从 1 通往 4,所以此时应该输出 "unconnected"。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
题解:队列优化Bellman-Ford算法(SPFA)
这题在昨天的打卡中已经有提到一般实现的Bellman-Ford算法,今天这里将用队列优化后的Bellman-Ford算法进行实现。
Bellman - Ford算法实现:
1、创建一个队列q,先将源点加入队列。
2、进入循环,当队列非空时,继续执行以下操作:
(1)从队列中取出队头节点node;
(2)标记该节点已从队列中取出;
(3)遍历当前节点的所有邻接边:
a.如果通过当前节点到达邻接节点的距离更短,则更新最短距离;
b.如果邻接节点不在队列中,则将其加入队列,并标记为已加入。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
struct Edge // 邻接表
{
int to; // 边的指向节点(边链接的节点 -- 邻接节点)
int val; // 边的权重
Edge(int t, int w) : to(t), val(w) {} // 构造函数,初始化边的指向节点和权重
};
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 创建一个邻接表,存储图的信息,大小为n+1,因为节点编号从1开始
vector<bool> inQueue(n + 1); // 用于标记节点是否已经在队列中(避免重复添加)
// 将所有边保存起来,构建邻接表
for (int i = 0; i < m; i++)
{
cin >> p1 >> p2 >> val;
grid[p1].push_back(Edge(p2, val)); // p1指向p2,边权重为val,将边添加到邻接表中
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX); // 初始化最短距离数组,所有节点到源点的最短距离初始为无穷大
minDist[start] = 0; // (除外)源点到自己的距离为0
// 队列优化Bellman-Ford算法
queue<int> q;
q.push(start); //先将起点加入队列
while (!q.empty())
{
int node = q.front(); // 取出队头节点 -- 作为后续邻接边的起始节点
q.pop();
inQueue[node] = false; // 标记该节点已从队列中取出
// 遍历当前节点的所有邻接边 -- 当前节点即是这些边的起始节点
for (Edge edge : grid[node])
{
int from = node;
int to = edge.to;
int value = edge.val;
if (minDist[to] > minDist[from] + value) // 开始松弛:如果通过当前节点到达邻接节点to的距离更短,则更新邻接节点to到源点的最短距离
{
minDist[to] = minDist[from] + value;
if (inQueue[to] == false) // 如果该节点不在队列中,则加入队列,并标记为已加入
{
q.push(to);
inQueue[to] = true;
}
}
}
}
if (minDist[end] == INT_MAX)
cout << "unconnected" << endl; // 不能到达终点
else
cout << minDist[end] << endl; // 到达终点最短路径
}题目二:卡码网 95. 城市间货物运输 II
题目链接
95. 城市间货物运输 II (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
然而,在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时,存在一种情况:图中可能出现负权回路。负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴,算法还需检测这种特殊情况。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
城市 1 到城市 n 之间可能会出现没有路径的情况
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
输出描述
如果没有发现负权回路,则输出一个整数,表示从城市
1到城市n的最低运输成本(包括政府补贴)。如果该整数是负数,则表示实现了盈利。如果发现了负权回路的存在,则输出 "circle"。如果从城市 1 无法到达城市 n,则输出 "unconnected"。输入示例
4 4 1 2 -1 2 3 1 3 1 -1 3 4 1输出示例
circle提示信息
路径中存在负权回路,从 1 -> 2 -> 3 -> 1,总权值为 -1,理论上货物运输商可以在该回路无限循环赚取政府补贴,所以输出 "circle" 表示已经检测出了该种情况。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
题解: 队列优化Bellman-Ford算法(SPFA)
这题是bellman-ford算法判断负权回路的应用。
和上一题相比较,区别也就在于对负权回路的判断,其余思路保持一致。
故这里有一个关键,即如何判断负权回路:
我们用计数器记录每个节点加入队列的次数。如果某个节点的计数器达到了n(即所有节点的数量),那么这个节点在经过V-1次松弛操作后,仍然可以通过负权边继续进行松弛。这违反了Bellman-Ford算法的假设,即在V-1次松弛操作后,最短路径应该已经被找到。因此,可以判断出图中存在负权回路。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
struct Edge // 邻接表
{
int to; // 边的指向节点(边链接的节点 -- 邻接节点)
int val; // 边的权重
Edge(int t, int w) : to(t), val(w) {} // 构造函数,初始化边的指向节点和权重
};
int main()
{
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 创建一个邻接表,存储图的信息,大小为n+1,因为节点编号从1开始
vector<bool> inQueue(n + 1); // 用于标记节点是否已经在队列中(避免重复添加)
// 将所有边保存起来,构建邻接表
for (int i = 0; i < m; i++)
{
cin >> p1 >> p2 >> val;
grid[p1].push_back(Edge(p2, val)); // p1指向p2,边权重为val,将边添加到邻接表中
}
int start = 1; // 起点(源点)
int end = n; // 终点
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0;
queue<int> q;
q.push(start); // 队列里放入起点
vector<int> count(n + 1, 0); // 创建一个计数器数组,用于记录每个节点加入队列的次数
count[start]++; // 刚放入一次起点,计数+1
bool flag = false; // 设置一个标志,用于标记是否找到了负权回路,初始化为false
while (!q.empty())
{
int node = q.front();
q.pop();
for (Edge edge : grid[node])
{
int from = node;
int to = edge.to;
int value = edge.val;
if (minDist[to] > minDist[from] + value) // 开始松弛:如果通过当前节点到达邻接节点to的距离更短,则更新邻接节点to到源点的最短距
{
minDist[to] = minDist[from] + value;
q.push(to);
count[to]++;
if (count[to] == n) // 关键:如果加入队列次数超过n-1次,就说明该图与负权回路
{
flag = true;
while (!q.empty())
q.pop();
break;
}
}
}
}
if (flag) // 如果存在负权回路,输出"circle"
cout << "circle" << endl;
else if (minDist[end] == INT_MAX)
cout << "unconnected" << endl;
else
cout << minDist[end] << endl;
}
题目三:卡码网 96. 城市间货物运输 III
题目链接
96. 城市间货物运输 III (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
输出描述
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
输入示例
6 7 1 2 1 2 4 -3 2 5 2 1 3 5 3 5 1 4 6 4 5 6 -2 2 6 1输出示例
0提示信息
从 2 -> 5 -> 6 中转一站,运输成本为 0。
1 <= n <= 1000;
1 <= m <= 10000;
-100 <= v <= 100;
题解: Bellman-Ford算法
这题是bellman_ford算法解决单源有限最短路问题的应用。
这题Bellman - Ford算法实现的关键在于:
使用minDist_copy来保留上一次迭代的结果,从而避免重复计算和比较,提高算法的效率。如果在当前迭代中没有发现新的更短路径,那么在接下来的迭代中,可以只检查minDist_copy是否已经包含了一条更短的路径,如果没有,那么就不需要更新minDist数组。
通过进行k + 1次松弛操作,每次迭代开始时,将当前的minDist数组的内容复制到minDist_copy中。 遍历所有边,进行松弛操作。如果在松弛过程中发现通过某个节点到达某个邻接节点的距离更短,则更新最短距离。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int src, dst, k, p1, p2, val, m, n; // 起点src,终点dst,松弛次数k
cin >> n >> m;
vector<vector<int>> grid; // 创建一个二维向量grid,用于存储图的信息:每个元素都是一条边(包含起始点,终止点,权值)
// 读取所有边,并添加到grid中
for (int i = 0; i < m; i++)
{
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1, INT_MAX); // 用于存储从起点到每个节点的最短距离,都初始化为最大值INT_MAX
minDist[src] = 0; // 起点除外,起点到本身的距离为0
vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果
// 进行k次松弛操作
for (int i = 1; i <= k + 1; i++)
{
minDist_copy = minDist; // 将上一次计算的结果赋值给minDist_copy:即将当前的minDist数组的内容复制到一个新的数组minDist_copy中
// 遍历所有边,进行松弛操作
for (vector<int> &side : grid)
{
int from = side[0];
int to = side[1];
int price = side[2];
// 注意使用 minDist_copy 来计算 minDist
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price)
{
minDist[to] = minDist_copy[from] + price;
}
}
}
if (minDist[dst] == INT_MAX) // 不能到达终点
cout << "unreachable" << endl;
else
cout << minDist[dst] << endl; // 到达终点最短路径
}