代码随想录算法训练营 | 二叉树理论基础

二叉树理论基础

二叉树的种类

满二叉树

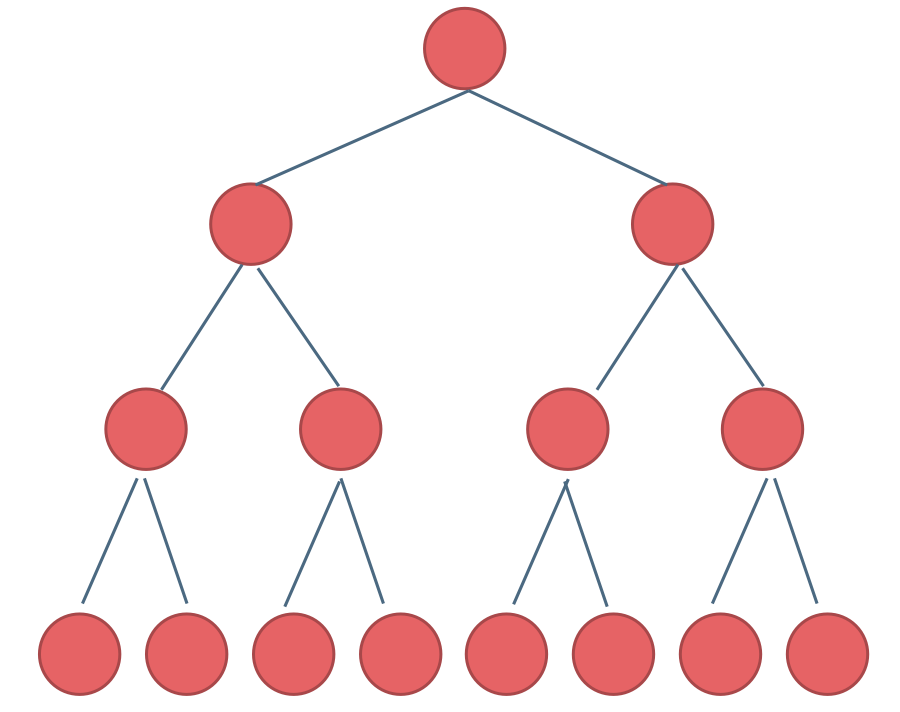
满二叉树的每个节点要么是叶子节点，要么拥有两个子节点，并且所有叶子节点都处于同一层。

如果一个满二叉树的高度为 h，那么它有2^h-1个节点。

完全二叉树

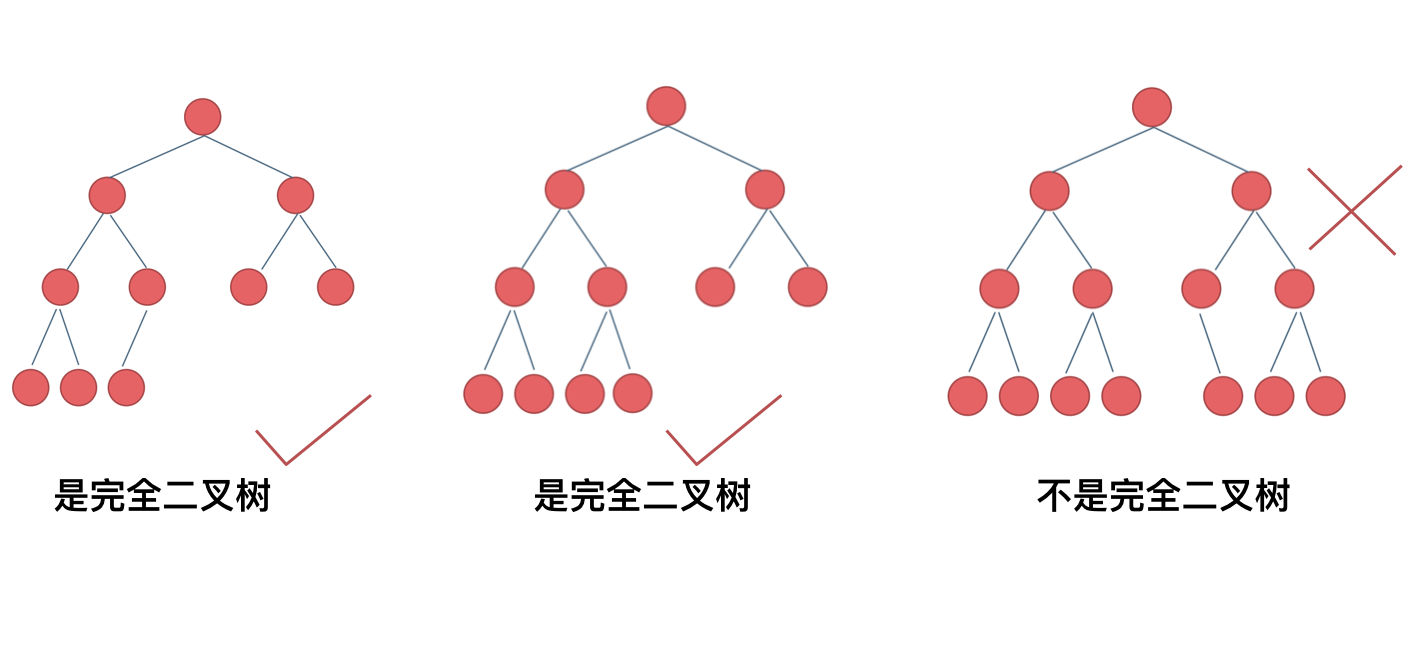
完全二叉树除了最后一层之外，每一层都是完全填满的，而且最后一层的所有节点都从左往右以此排列，中间不允许出现空缺。

与满二叉树不同，完全二叉树允许最后一层不满，但节点必须尽量靠左。

设层数为 h，每一层包含1~2^h-1个节点。

二叉搜索树

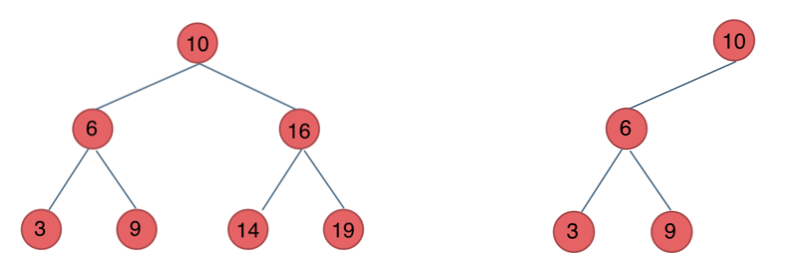
二叉搜索树是一个有序树。

• 对于任意一个节点 N，左子树中所有节点的值都小于 N 的值。
• 对于任意一个节点 N，右子树中所有节点的值都大于 N 的值。
• 左右子树本身也都是二叉搜索树。

平衡二叉搜索树

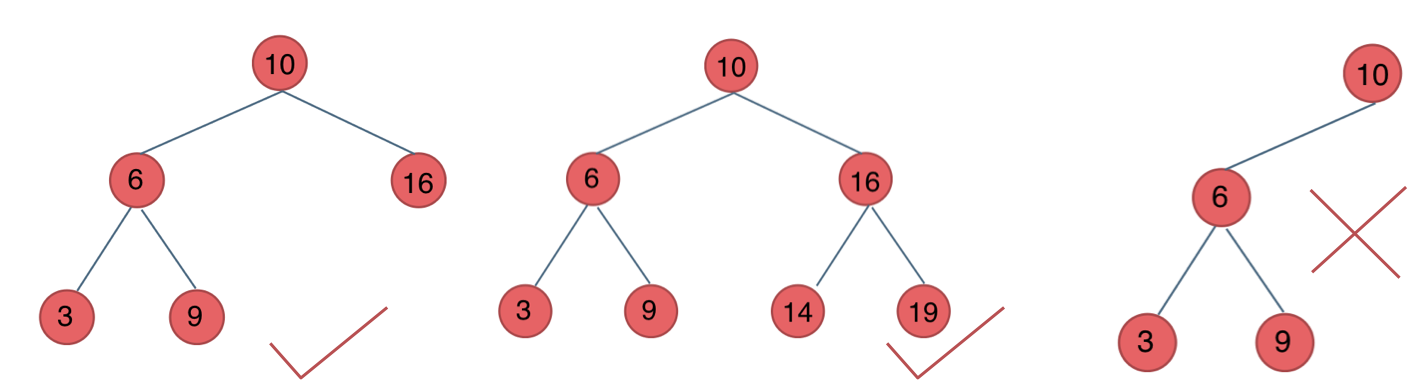
对于平衡二叉树中的每个节点，其左右子树的高度差不超过1，并且左右两个子树都是一棵平衡二叉树。（或者是一颗空树）

平衡二叉搜索树（AVL树），既要满足二叉搜索树的排序特性，又要满足平衡二叉树的平衡性。

二叉树存储方式

链式存储

链式存储使用指针，通过指针把分布在各个地址的节点串联一起：

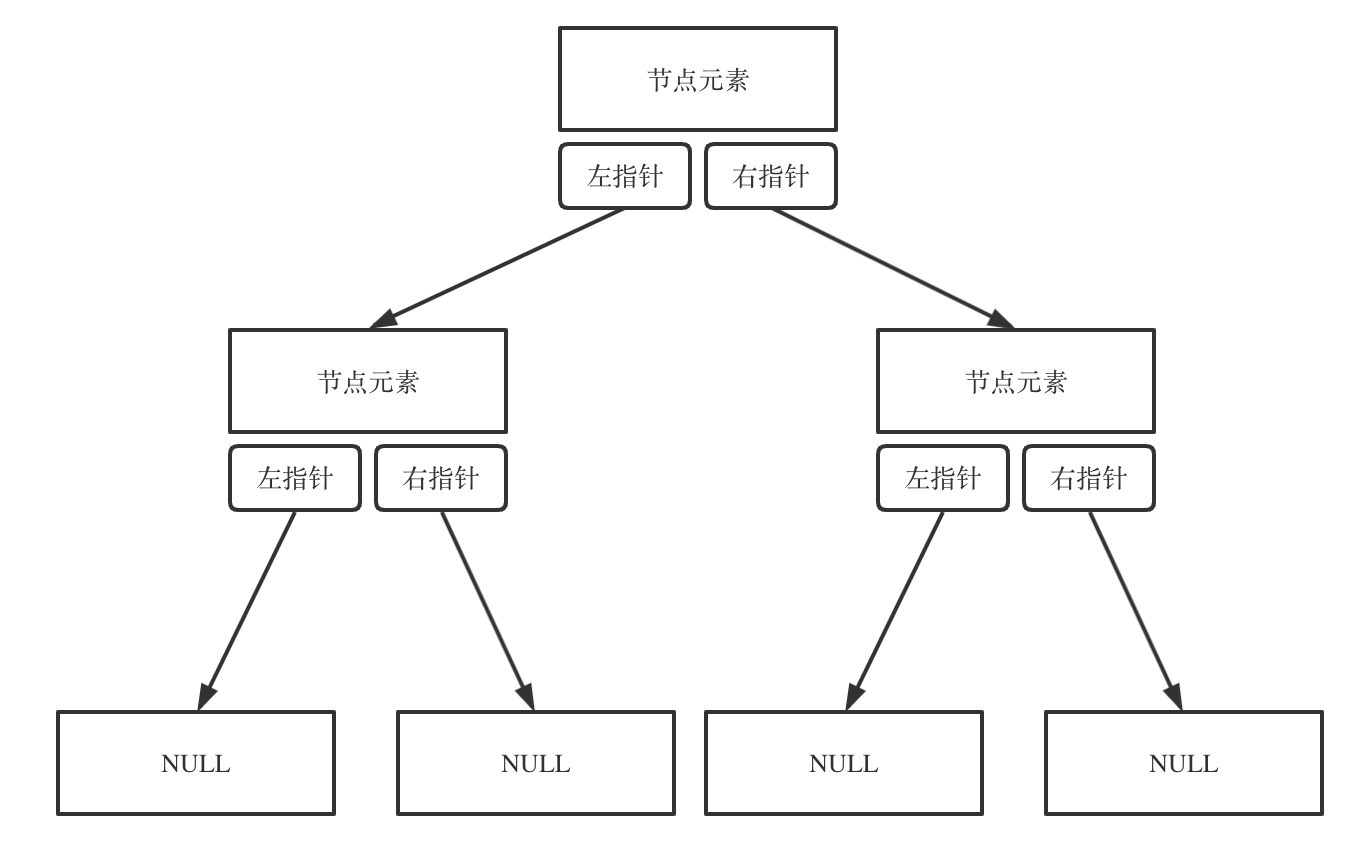
顺序存储

顺序存储使用数组，常用于完全二叉树。

对于一个存储在数组 arr 中的二叉树节点，父节点、左子节点、右子节点的关系如下：

• 父节点索引：i
• 左子节点索引：2 * i + 1
• 右子节点索引：2 * i + 2

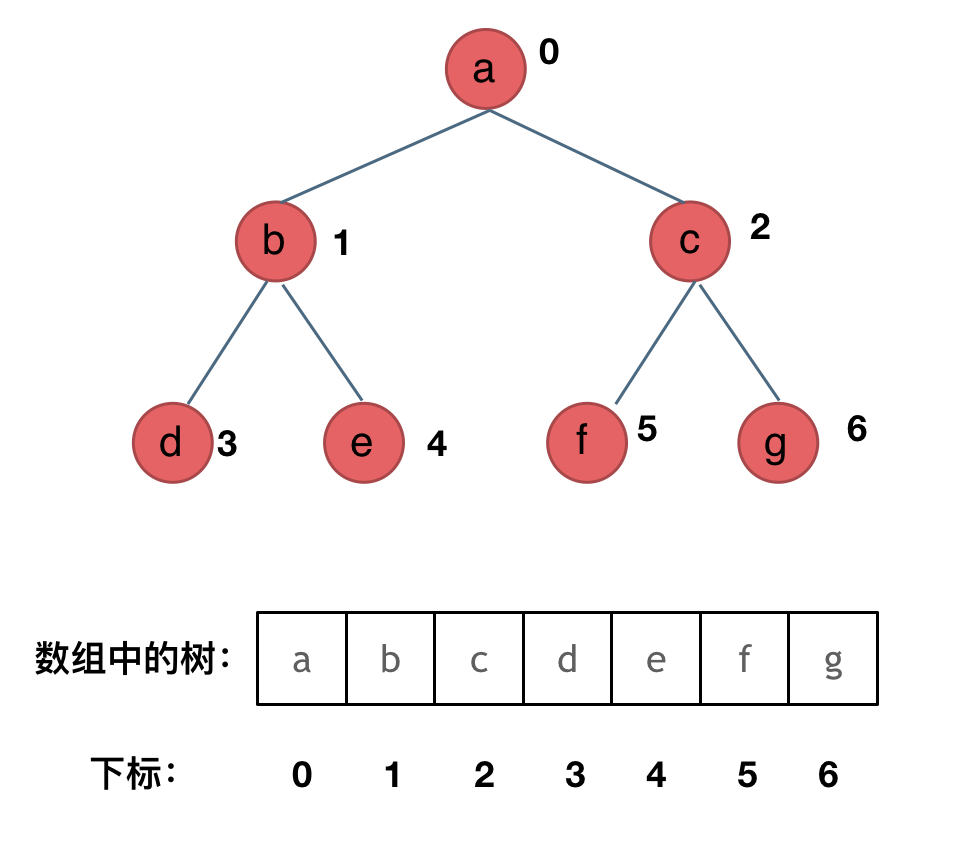
二叉树遍历方式

深度优先搜索

沿着一个分支一直遍历到叶子节点，然后回溯，继续遍历其他分支，分为前序遍历、中序遍历和后序遍历，一般借助栈使用递归法。

名字里的前中后指的是中间节点的遍历顺序

• 前序遍历：根节点 → 左子树 → 右子树

• 中序遍历：左子树 → 根节点 → 右子树

• 后序遍历：左子树 → 右子树 → 根节点

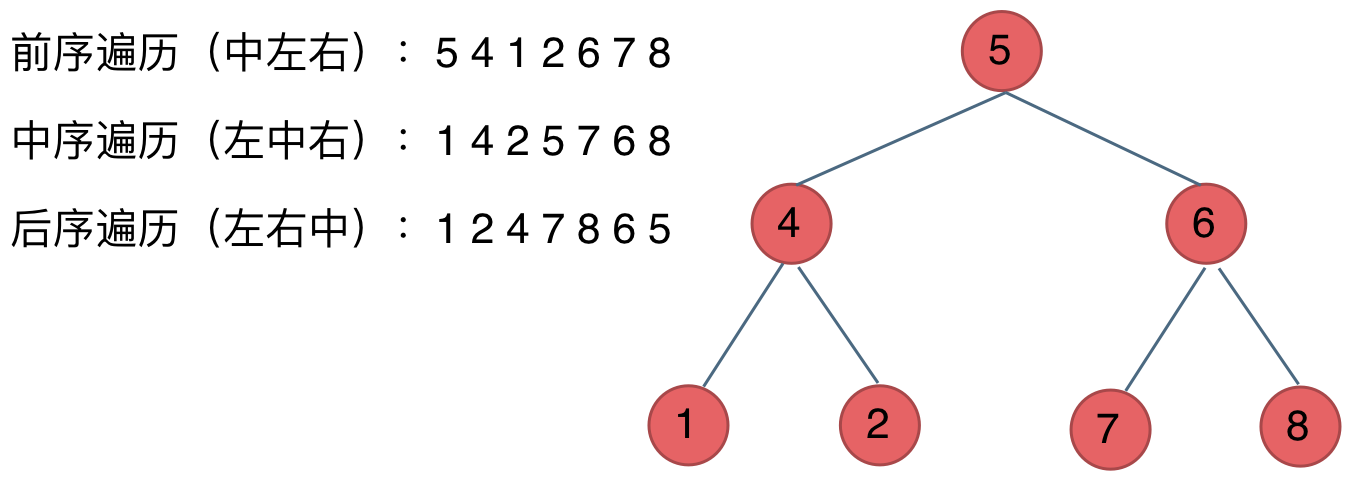
广度优先搜索

层序遍历，按层从左到右访问每一层的节点，通常使用队列实现。

二叉树的定义

链式存储定义如下：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}