1.单值二叉树

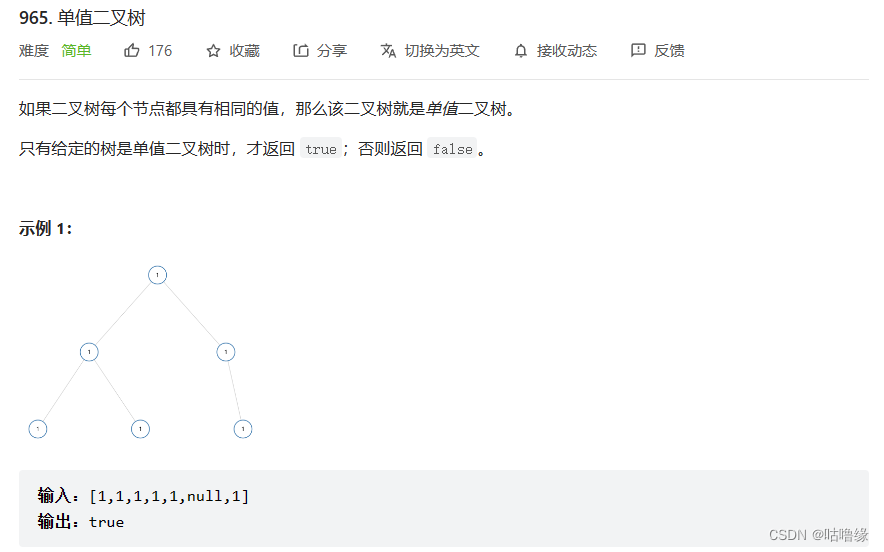
bool isUnivalTree(struct TreeNode* root)
{
    if(root==NULL)//判空 如果root为空指针那么也就是说比较结束了，所以返回true
    {
        return true;
    }
    if(root->left&&root->left->val!=root->val)
    //判断root->left不为空并且值不相等返回false
    {
        return false;
    }
    if(root->right&&root->right->val!=root->val)
    //同上
    {
        return false;
    }
    return isUnivalTree(root->right)&&isUnivalTree(root->left);
    //若左右孩子有一个值为false则整个函数结果返回false
}

2.相同的树

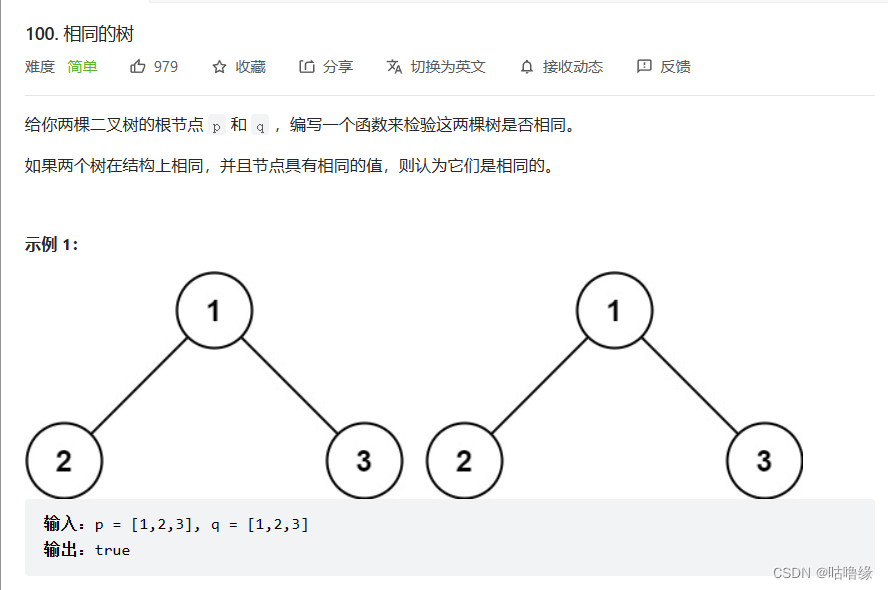
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)//如果两个节点都同时为空则意味着走到尾了，完全相同
    {
        return true;
    }
   
    else if(p==NULL||q==NULL)//反之排除上面的情况如果有一个节点为空则返回false
    {
        return false;
    }
    if(p->val!=q->val)//递归要写判定结束条件，不相等返回false
    {
        return false;
    }
  
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
    //若有一个不成立则返回false
}

3.对称二叉树

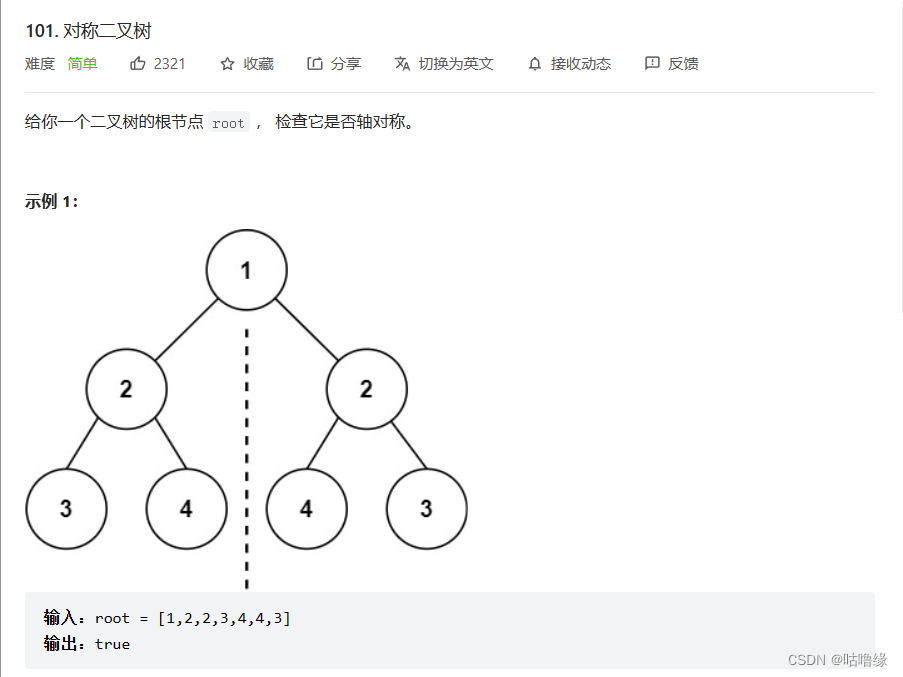
这道题的话就转载一段话吧 出自这道题的评论区，我的解法和上道题有异曲同工之妙

递归的难点在于：找到可以递归的点 为什么很多人觉得递归一看就会，一写就废。 或者说是自己写无法写出来，关键就是你对递归理解的深不深。

对于此题： 递归的点怎么找？从拿到题的第一时间开始，思路如下：

1.怎么判断一棵树是不是对称二叉树？ 答案：如果所给根节点，为空，那么是对称。如果不为空的话，当他的左子树与右子树对称时，他对称

2.那么怎么知道左子树与右子树对不对称呢？在这我直接叫为左树和右树 答案：如果左树的左孩子与右树的右孩子对称，左树的右孩子与右树的左孩子对称，那么这个左树和右树就对称。

仔细读这句话，是不是有点绕？怎么感觉有一个功能A我想实现，但我去实现A的时候又要用到A实现后的功能呢？

当你思考到这里的时候，递归点已经出现了： 递归点：我在尝试判断左树与右树对称的条件时，发现其跟两树的孩子的对称情况有关系。

想到这里，你不必有太多疑问，上手去按思路写代码，函数A（左树，右树）功能是返回是否对称

def 函数A（左树，右树）： 左树节点值等于右树节点值 且
函数A（左树的左子树，右树的右子树），函数A（左树的右子树，右树的左子树）均为真 才返回真

实现完毕。。。

写着写着。。。你就发现你写出来了。。。。。。

bool issame(struct TreeNode*p,struct TreeNode*q)
{
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    else if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;

    }
    return issame(p->left,q->right)&&issame(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){
    return issame(root,root);

}

3.二叉树的最大深度

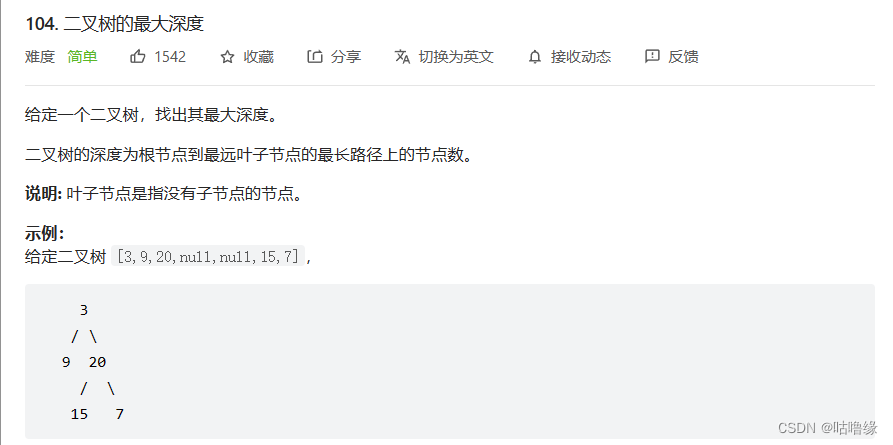
int maxDepth(struct TreeNode* root){
    if(root==NULL)
    {
        return 0;
    }
    int leftdeep=maxDepth(root->left);
    int rightdeep=maxDepth(root->right);
    return leftdeep>rightdeep? leftdeep+1:rightdeep+1;

}