当前位置：首页 > article >正文

代码随想录_刷题笔记_第三次

article 2024/11/17 16:25:58

字符串 — KMP算法（理论）

**解决问题：**字符串匹配的问题（eg：文本串 aabaabaaf 模式串 aabaaf 求在文本串中是否出现过模式串）

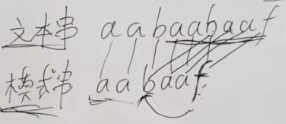
**暴力匹配：**当 b 和 f 不匹配时，整体向后跳一位再进行匹配

**KMP：**当 b 和 f 不匹配时，找到 b，从 b 向后继续进行比对（找到 b，这依赖于前缀表）

前缀与后缀： aabaaf：前缀（包含首字符而不包含尾字符的所有子串，a、aa、aab、aaba、aabaa）后缀（包含尾字符而不包含首字符的所有子串，f、af、aaf、baaf、abaaf）

最长相等前后缀（长度）： a（0）aa（1）aab（0）aaba（1）aabaa（2）aabaaf（0）

**前缀表（next数组）：**aabaaf（010120）

**使用前缀表的匹配过程：**aabaaf，当到 f 不匹配时，通过前缀表得到前面字符串 aabaa 的最长相等前后缀长度 2，所以接下来从最长相等前缀的后面 b 继续进行匹配

字符串 — KMP算法（代码）

aabaaf

010120

next数组具体代码：

初始化

i : 指向后缀末尾位置
j : 指向前缀末尾位置（ i 之前的字符串包括 i 的最长相等前后缀的长度）

j = 0;
next[0] 0;
for(int i = 1; i < s.size(); i++){...}

处理前后缀（首字符和尾字符）不相同的情况

// 当前后缀不相同时，回退，回退到前缀对应字符的前一个字符，其在前缀表中所对应的位置
// 有可能需要多次回退，所以不能使用 if，要使用 while
while(j > 0 && s[i] != s[j]){
	j = s[j - 1];
}

处理前后缀相同的情况

// 最长相等前后缀长度 + 1 : j++
if(s[i] = s[j]) j++;

更新next数组的值
```
next[i] = j;
```

整体代码：

void getNext (int* next, const string& s){
	int j = 0;
	next[0] = 0;
	for(int i = 1;i < s.size(); i++){
		// 前后缀不相等时，回退（这里有可能是一个连续回退的操作）
		while(j > 0 && s[i] != s[j]) {
			j = next[j - 1];
		}	
		// 前后缀相同时
		if(s[i] == s[j]) {
			j++;
		}
		// 更新 next 数组
		next[i] = j;
	}
}

字符串 — 重复的字符串

题目链接：459. 重复的子字符串 - 力扣（LeetCode）

**题目要求：**给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成

示例 1:

输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。

示例 2:

输入: s = "aba"
输出: false

示例 3:

输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)

思路： KMP算法

ababababab 它的前缀表是 0012345678，所以 len - next[len - 1] 的值为 2，刚好是重复字符串的长度，并且 len % 2 == 0

解法：

class Solution {
public:
    void getnext(int* next, const string& s){
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++){
            while(j > 0 && s[i] != s[j]){   // while: 连续回退操作
                j = next[j - 1];
            }
            if(s[i] == s[j]){
                j++;
            }
            next[i] = j;
        }
    }

    bool repeatedSubstringPattern(string s) {
        if(s.size() == 0){   // 空字符串直接返回 false
            return false;
        }
        int len = s.size();
        int next[len];   // 前缀表
        getnext(next, s);
        if(next[len - 1] != 0 && len % (len - next[len - 1]) == 0){
            return true;
        }else{
            return false;
        }
    }
};

栈与队列 — 用栈实现队列

题目链接：232. 用栈实现队列 - 力扣（LeetCode）

题目要求：

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

**思路：**栈（先入后出）、队列（先入先出）使用两个栈来模拟队列，将从第一个栈中取出的元素放入第二个栈中（一旦有取出操作，就是取出全部元素），再从第二个栈取出元素，这样就变成了先入先出

解法：

class MyQueue {
public:
    stack<int> in;  
    stack<int> out;

    MyQueue() {

    }
    
    void push(int x) {
        in.push(x); 
    }
    
    int pop() {
        if(out.empty()){          // 只有当第二个栈为空时，才向它放入元素
            while(!in.empty()){   // 将第一个栈中所有元素全部放入
                out.push(in.top());
                in.pop();
            }
        }
        int result = out.top(); // 得到栈顶元素
        out.pop();              // 移除栈顶元素
        return result;
    }
    
    int peek() {
        int result = this->pop();
        out.push(result);   // pop 不仅得到元素还移除元素
        return result; 
    }
    
    bool empty() {
        return in.empty() && out.empty();
    }
};

栈与队列 — 用队列实现栈

题目链接：225. 用队列实现栈 - 力扣（LeetCode）

题目要求：

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

**思路：**使用一个队列来模拟栈，将队列中除了最后一个元素的所有元素全部弹出再重新加入，取出最后一个元素

解法：

class MyStack {
public:
    queue<int> que;

    MyStack() {

    }
    
    void push(int x) {
        que.push(x);
    }
    
    int pop() {
        int len = que.size();
        len--;   // 最后一个元素不进行添加再移除的操作
        while(len--){
            que.push(que.front());   // 添加
            que.pop();   // 移除
        }
        int result = que.front();
        que.pop();
        return result;
    }
    
    int top() {
        int len = que.size();
        len--;   // 最后一个元素不进行添加再移除的操作
        while(len--){
            que.push(que.front());   // 添加
            que.pop();   // 移除
        }
        int result = que.front(); 
        que.push(que.front());   // 对最后一个元素进行添加移除操作
        que.pop();
        return result;
    }
    
    bool empty() {
        return que.empty();
    }
};

栈 — 有效的括号

题目链接：20. 有效的括号 - 力扣（LeetCode）

题目要求：

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例：

输入：s = "()"
输出：true

输入：s = "()[]{}"
输出：true

输入：s = "(]"
输出：false

输入：s = "()[{]}
输出：false

思路：

不匹配只有三种情况：左括号多，右括号多，左括号与右括号匹配不上

使用栈：遇到左括号，将它对应的右括号放入栈中，遇到右括号，从栈中取出相同的右括号消除（若没有则返回错误）（若最后栈中还有元素则返回错误）

解法：

class Solution {
public:
    bool isValid(string s) {
        if(s.size() % 2 != 0){
            return false;
        }
        stack<char> st;
        for(int i = 0; i < s.size(); i++){
            // 前三种是左括号，后面是右括号
            if(s[i] == '(')         st.push(')');
            else if(s[i] == '{')    st.push('}');
            else if(s[i] == '[')    st.push(']'); 
            else if(st.empty() || st.top() != s[i])    return false;
            else    st.pop();
        }
        return st.empty();    // 如果最后为空，就代表着完全匹配成功
    }
};

栈 — 删除字符串中所有相邻重复项

题目链接：1047. 删除字符串中的所有相邻重复项 - 力扣（LeetCode）

题目要求：

给出由小写字母组成的字符串 s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 s 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

**思路：**使用栈

解法：

class Solution {
public:
    string removeDuplicates(string s) {
        stack<int> st;
        for(char str : s){
            if(st.empty() || st.top() != str){
                st.push(str);
            }else{
                st.pop();   // 当相同时消除元素
            }
        }
        string result = "";
        while(!st.empty()){
            result += st.top();   // 字符串拼接操作
            st.pop();
        }
        reverse(result.begin(), result.end());   // 反转字符串
        return result; 
    }
};

栈 — 逆波兰表达式求值

题目链接：150. 逆波兰表达式求值 - 力扣（LeetCode）

题目要求：

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = 22

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

解法：

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<long long> st; 
        for (int i = 0; i < tokens.size(); i++) {
            if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
                long long num1 = st.top();
                st.pop();
                long long num2 = st.top();
                st.pop();
                if (tokens[i] == "+") st.push(num2 + num1);
                if (tokens[i] == "-") st.push(num2 - num1);
                if (tokens[i] == "*") st.push(num2 * num1);
                if (tokens[i] == "/") st.push(num2 / num1);
            } else {
                st.push(stoll(tokens[i]));
            }
        }
        int result = st.top();
        st.pop(); 
        return result;
    }
};

队列 — 滑动窗口最大值

题目链接：239. 滑动窗口最大值 - 力扣（LeetCode）

题目要求：

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

**思路：**利用双向队列构造单调队列（从大到小），使用双向队列队列保存滑动窗口，但是只维护最大值，当向尾部移动添加新值时，删除所有小于新值的值（这样每一次头部都是队列中的最大值），下面以示例一的过程为例

[3, -1]，[3, -1, -3]，[5]，[5, 3]，[6]，[7]

最后的答案就是每次队列的第一项：335567

解法：

class Solution {
private:
    class MyQueue { //单调队列（从大到小）
    public:
        deque<int> que;   // 双向队列

        // 只有在移除的元素刚好是队列的头部，也就是最大值的时候才会移除头部元素
        void pop(int value) {
            if (!que.empty() && value == que.front()) {
                que.pop_front();   
            }
        }

        // 向队列中加入元素，同时删除队列中所有小于这个元素的项
        void push(int value) {
            while (!que.empty() && value > que.back()) {
                que.pop_back();
            }
            que.push_back(value);

        }

        // 返回队列中的最大值，此时其实就是头部元素
        int front() {
            return que.front();
        }
    };

public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MyQueue que;
        vector<int> result;
        for (int i = 0; i < k; i++) {   // 先将前k的元素放进队列
            que.push(nums[i]);
        }
        result.push_back(que.front());   // result 记录前k的元素的最大值
        for (int i = k; i < nums.size(); i++) {
            que.pop(nums[i - k]);   // 滑动窗口移除最前面元素
            que.push(nums[i]);      // 滑动窗口前加入最后面的元素
            result.push_back(que.front());   // 记录对应的最大值
        }
        return result;
    }
};

队列 — 前K个高频元素

题目链接：347. 前 K 个高频元素 - 力扣（LeetCode）

**题目要求：**给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

**思路：**使用 map，key 保存元素，value 保存元素出现的次数，根据 value 进行从大到小排序

对排序操作可以使用优先级队列（也可以使用快排：将 map 转换成 vector 的结构体，然后对整个数组进行排序，但是优先级队列是最优解）

优先级队列要用小根堆，只保存 k 个元素，弹出的元素是值最小的，也就是出现频率最低的元素，那么最后剩下的就是频率最高的前k个

解法：

class Solution {
public:
    // 小顶堆
    class mycomparison {
    public:
        // 运算符重载() : 比较第一个键值和第二个键值对的 value 值
        bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
            return lhs.second > rhs.second;
        }
    };

    vector<int> topKFrequent(vector<int>& nums, int k) {
        // 要统计元素出现频率
        unordered_map<int, int> map; // map<nums[i],对应出现的次数>
        for (int i = 0; i < nums.size(); i++) {
            map[nums[i]]++;
        }

        // 对频率排序
        // 定义一个小顶堆，大小为k
        // 参数：堆中的数据类型、堆中数据的存储地方、存储方式（大根堆、小根堆）
        priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;

        // 用固定大小为k的小顶堆，扫面所有频率的数值
        for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
            pri_que.push(*it);   // 往堆中放入元素
            if (pri_que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
                pri_que.pop();   // 小根堆，弹出的元素是值最小的
            }
        }

        // 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组
        vector<int> result(k);
        for (int i = k - 1; i >= 0; i--) {
            result[i] = pri_que.top().first;
            pri_que.pop();
        }
        return result;
    }
};

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> map;
        vector<int> result;
        for(int num : nums){
            map[num]++;         // 将数据放入 map 中
        }
        // 将 map 转换为 vector<pair<int, int>>
        vector<pair<int, int>> vec(map.begin(), map.end());
        // 对 vec 进行排序，根据频率
        sort(vec.begin(), vec.end(), [](pair<int, int>&a, pair<int, int>&b){
            return a.second > b.second;
        });
        // 取出高频元素，放入 result 中
        for(auto pair : vec){
            if(k > 0) result.push_back(pair.first);
            k--;
        }
        return result;
    }
};

查看全文

http://www.kler.cn/a/324456.html