当前位置： 首页 > article >正文

2-3树（2-3 Tree）：原理、常见算法及其应用

article 2024/11/20 7:22:19

目录

引言

2-3树的基本概念

常见算法

查找节点

插入节点

删除节点

2-3树的应用场景

1. 文件系统目录管理

应用原理

场景描述

2. 字典编码

应用原理

场景描述

总结

优势对比

自平衡特性

灵活的节点结构

高效的操作性能

简单的实现

广泛的应用场景

数据一致性

引言

2-3树（2-3 Tree）是一种自平衡的二叉树，它允许节点拥有一个或两个键值，并且每个内部节点可以有2或3个子节点。这种数据结构保证了树的高度在最坏情况下为O(logn)，使得查找、插入和删除操作的时间复杂度均为)O(logn)。本文将从2-3树的基本概念出发，逐步介绍其原理、常见算法，并通过具体的Java代码示例来加深理解，最后探讨2-3树在算法中的实际应用场景，并总结2-3树的优势。

2-3树的基本概念

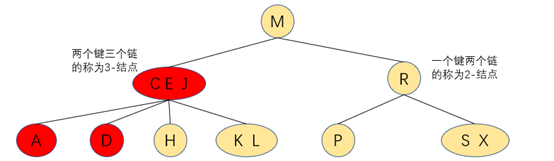
为了保证二叉树的平衡，提高树查找的效率，减少遍历的层级，我们允许一个结点保留多个键，并且链接的不止两条链

 　　

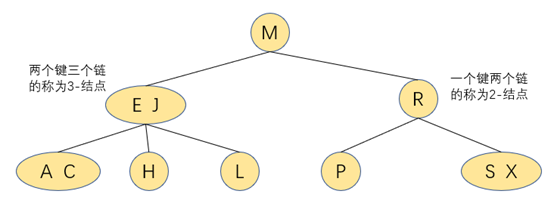
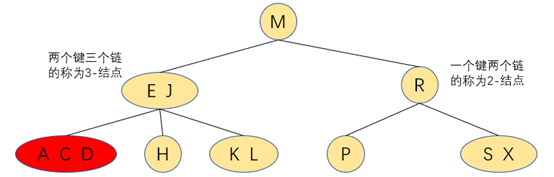
　　2-结点：

　　含有一个键和两条链，左链指向的键都小于该结点，右链指向的键都大于该结点

　　3-结点：

　　含有两个键和三条链，左链指向的键都小于该结点，右链指向的键都大于该结点，中链指向的的键介于该结点的两个键之间

特性

  • 树中每个节点最多有两个键值。
  • 每个节点至少有一个键值。
  • 对于每个节点，所有左子树的键值都小于该节点的键值。
  • 对于每个节点，所有右子树的键值都大于该节点的键值。
  • 对于包含两个键值的节点，中间子树的键值介于两个键值之间。

节点定义

class Node {
    int[] keys;
    Node[] children;
    boolean isLeaf;

    Node(int k1) {
        keys = new int[]{k1};
        children = new Node[2];
        isLeaf = true;
    }

    Node(int k1, int k2) {
        keys = new int[]{k1, k2};
        children = new Node[3];
        isLeaf = false;
    }
}

常见算法

public class TwoThreeTree {
    private Node root;

    public TwoThreeTree() {
        root = null;
    }

    // 插入新键值
    public void insert(int value) {
        root = insertRecursive(root, value);
        if (root.keys.length > 2) {
            // 如果根节点分裂，则创建新的根节点
            Node newRoot = new Node();
            newRoot.children[0] = root.children[0];
            newRoot.children[1] = new Node(root.keys[1]);
            newRoot.children[1].children[0] = root.children[1];
            newRoot.children[1].children[1] = root.children[2];
            newRoot.keys[0] = root.keys[1];
            root = newRoot;
        }
    }

    private Node insertRecursive(Node current, int value) {
        if (current == null) {
            if (value < current.keys[0]) {
                return new Node(value, current.keys[0]);
            } else {
                return new Node(current.keys[0], value);
            }
        }

        int i = 0;
        if (value < current.keys[0]) {
            current.children[i] = insertRecursive(current.children[i], value);
        } else if (current.keys.length == 2 && value > current.keys[0] && value < current.keys[1]) {
            current.children[i + 1] = insertRecursive(current.children[i + 1], value);
        } else {
            current.children[current.keys.length] = insertRecursive(current.children[current.keys.length], value);
        }

        if (current.children[i].keys.length == 2) {
            // 分裂节点
            int splitKey = current.children[i].keys[1];
            Node temp = new Node(current.children[i].keys[0]);
            current.children[i] = temp;
            current.keys[i] = splitKey;
            if (current.keys.length == 1) {
                current.keys[1] = current.children[i + 1].keys[0];
                current.children[i + 1] = new Node(current.children[i + 1].keys[1]);
            } else {
                Node newChild = new Node(current.children[i + 1].keys[0], splitKey);
                current.children[i + 1] = newChild;
                current.keys[i] = splitKey;
            }
        }

        return current;
    }
}

查找节点

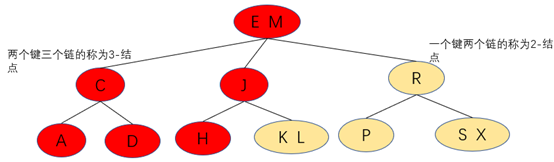
2-3树的查找思路与二叉查找树相似，对于需要查找的键，从根结点开始遍历，小于往左，大于则往右，当找到3-结点时，若查找的键介于3-结点的两个键之间，则找中链接对应的结点，命中则返回。

　　查找过程没命中时则继续递归查找子树。

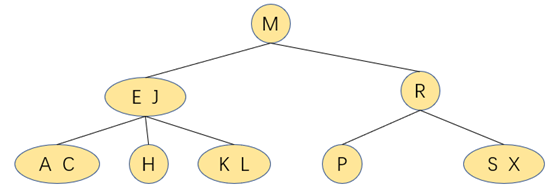
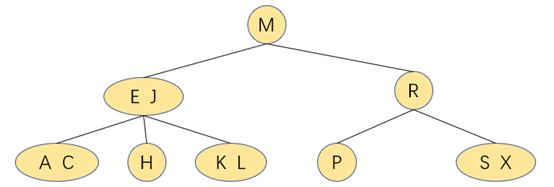
　　如图：查找键为H的结点，首先找根结点M，由于H<M，往下找左子树

 　　

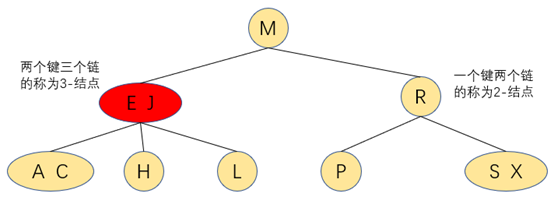
　　查找到左子树为3-结点，判断H>E并且H<J，则找中链结点的键

 　　

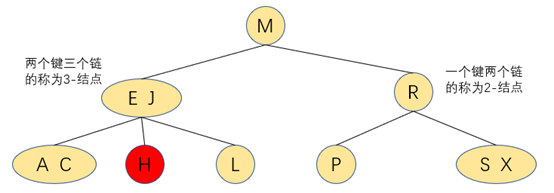
Java代码实现

public Node search(int value) {
    return searchRecursive(root, value);
}

private Node searchRecursive(Node current, int value) {
    if (current == null) {
        return null;
    }

    if (value == current.keys[0]) {
        return current;
    } else if (current.keys.length == 2 && value == current.keys[1]) {
        return current;
    } else if (value < current.keys[0]) {
        return searchRecursive(current.children[0], value);
    } else if (current.keys.length == 2 && value > current.keys[0] && value < current.keys[1]) {
        return searchRecursive(current.children[1], value);
    } else {
        return searchRecursive(current.children[current.keys.length], value);
    }
}

插入节点

往2-3树中插入结点的思路和二叉树一致，首先进行查找，根据2-3树的特性将结点挂到合适的位置，保持树的平衡。由于2-3树既包含2-结点同时也包含3-结点，因此在插入时针对不同类型的结点:

　　一、 往2-结点中插入新键

　　插入K：往2-结点中插入新键时，我们可以保证树层级不变的基础上，将2-结点转化为3-结点

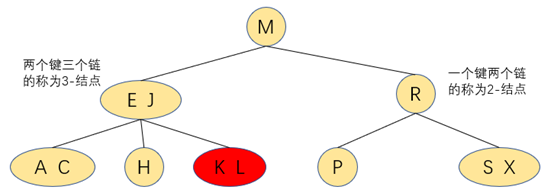
　　二、 往只有一个3-结点中插入新键

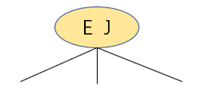
　　往3-根结点中插入S

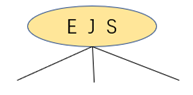
　　将中键提升为根结点，左右两键成为左右子树

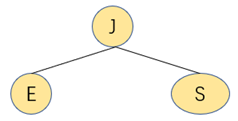
　　三、 往一个父结点为2-结点的3-结点中插入新键

　　往该2-3树中插入元素Z

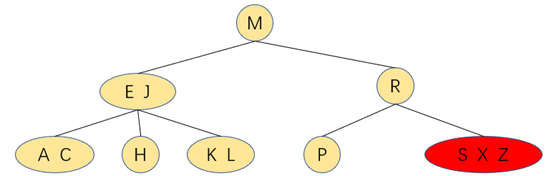
　　将3-结点的中间元素往上提

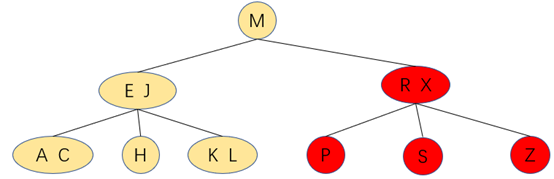
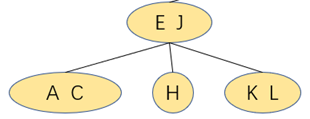
　　四、 往一个父结点为3-结点的3-结点中插入新键

　　往该2-3树中插入元素D

　　将插入后形成的3-结点往上提

　　将形成的3-父节点再次取中间值往上提升一层

　　五、 插入结点到根结点的路径上是3-结点

　　往该2-3树中插入D

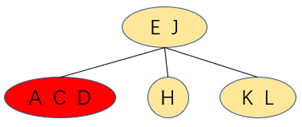
　　将插入后形成的3-结点取中间值往上提

 　　

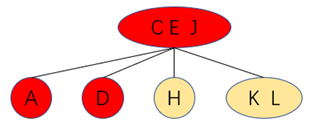
　　将形成的3-根结点再次分解

 　　

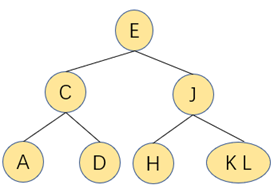
Java代码实现

public class TwoThreeTree {
    private Node root;

    public TwoThreeTree() {
        root = null;
    }

    // 插入新键值
    public void insert(int value) {
        root = insertRecursive(root, value);
        if (root.keys.length > 2) {
            // 如果根节点分裂，则创建新的根节点
            Node newRoot = new Node();
            newRoot.children[0] = root.children[0];
            newRoot.children[1] = new Node(root.keys[1]);
            newRoot.children[1].children[0] = root.children[1];
            newRoot.children[1].children[1] = root.children[2];
            newRoot.keys[0] = root.keys[1];
            root = newRoot;
        }
    }

    private Node insertRecursive(Node current, int value) {
        if (current == null) {
            if (value < current.keys[0]) {
                return new Node(value, current.keys[0]);
            } else {
                return new Node(current.keys[0], value);
            }
        }

        int i = 0;
        if (value < current.keys[0]) {
            current.children[i] = insertRecursive(current.children[i], value);
        } else if (current.keys.length == 2 && value > current.keys[0] && value < current.keys[1]) {
            current.children[i + 1] = insertRecursive(current.children[i + 1], value);
        } else {
            current.children[current.keys.length] = insertRecursive(current.children[current.keys.length], value);
        }

        if (current.children[i].keys.length == 2) {
            // 分裂节点
            int splitKey = current.children[i].keys[1];
            Node temp = new Node(current.children[i].keys[0]);
            current.children[i] = temp;
            current.keys[i] = splitKey;
            if (current.keys.length == 1) {
                current.keys[1] = current.children[i + 1].keys[0];
                current.children[i + 1] = new Node(current.children[i + 1].keys[1]);
            } else {
                Node newChild = new Node(current.children[i + 1].keys[0], splitKey);
                current.children[i + 1] = newChild;
                current.keys[i] = splitKey;
            }
        }

        return current;
    }
}

删除节点

删除节点时需要考虑三种情况：

  1. 节点是一个叶节点。
  2. 节点是一个2-节点。
  3. 节点是一个3-节点。

Java代码实现

public void delete(int value) {
    root = deleteRecursive(root, value);
    if (root.keys.length == 0) {
        // 如果根节点为空，则删除根节点
        root = root.children[0];
    }
}

private Node deleteRecursive(Node current, int value) {
    if (current == null) {
        return null;
    }

    if (value == current.keys[0]) {
        // 删除2-节点或3-节点的第一个键值
        if (current.isLeaf) {
            // 删除叶节点
            if (current.keys.length == 2) {
                current.keys[0] = current.keys[1];
                current.keys[1] = 0;
            }
            current.keys[0] = 0;
            return current;
        } else {
            // 替换键值后删除
            int replacement = findMin(current.children[0]);
            current.keys[0] = replacement;
            current.children[0] = deleteRecursive(current.children[0], replacement);
            return current;
        }
    } else if (current.keys.length == 2 && value == current.keys[1]) {
        // 删除3-节点的第二个键值
        if (current.isLeaf) {
            current.keys[1] = 0;
            return current;
        } else {
            int replacement = findMin(current.children[2]);
            current.keys[1] = replacement;
            current.children[2] = deleteRecursive(current.children[2], replacement);
            return current;
        }
    } else if (value < current.keys[0]) {
        current.children[0] = deleteRecursive(current.children[0], value);
        return current;
    } else if (current.keys.length == 2 && value > current.keys[0] && value < current.keys[1]) {
        current.children[1] = deleteRecursive(current.children[1], value);
        return current;
    } else {
        current.children[current.keys.length] = deleteRecursive(current.children[current.keys.length], value);
        return current;
    }
}

private int findMin(Node node) {
    while (node.children[0] != null) {
        node = node.children[0];
    }
    return node.keys[0];
}

2-3树的应用场景

1. 文件系统目录管理

2-3树可以用于文件系统的目录管理，以加速文件查找速度。

应用原理
  • 文件系统的目录项作为键值存储在2-3树的节点中。
  • 查找文件时，根据文件名在树中查找对应的文件元数据。
  • 插入和删除文件时，自动调整树的结构，保持较低的高度。
场景描述

在文件系统中，为了快速查找文件，可以使用2-3树来组织目录结构。当用户访问文件时，根据文件名可以在树中迅速定位到文件的位置，而不需要遍历整个目录结构。2-3树的自平衡特性确保了目录结构的高效性，即使在频繁的文件操作下也能保持良好的性能。

2. 字典编码

在字典编码中，2-3树可以用来存储单词及其解释。

应用原理
  • 单词作为键值存储在2-3树的节点中。
  • 单词的解释和其他相关信息作为键值对应的数据存储。
  • 用户在查询单词时，根据单词名称快速查找、插入或更新相应的信息。
场景描述

在开发电子词典或在线词典时，可以利用2-3树来管理单词及其解释。用户在查询单词时，可以通过2-3树快速定位到所需的信息。此外，2-3树还可以用于实现自动补全等功能，提高用户体验。2-3树的自平衡特性使得在处理大量的词汇时依然保持高效。

总结

2-3树作为一种高效的数据结构，在计算机科学中有广泛的应用。通过允许节点拥有一个或两个键值来保持树的平衡，2-3树在最坏的情况下也能够保证操作的时间复杂度为O(logn)。掌握2-3树的概念和相关算法对于深入理解计算机科学的核心知识至关重要。

优势对比

自平衡特性
  • 2-3树：通过分裂和合并操作来保持树的平衡，确保了树的高度在最坏情况下为O(logn)，使得查找、插入和删除操作的时间复杂度均为O(logn)。
灵活的节点结构
  • 2-3树：允许节点拥有一个或两个键值，提供了比传统二叉树更多的灵活性，特别是在处理大量数据时。
高效的操作性能
  • 2-3树：由于自平衡特性，它在频繁的插入和删除操作下依然保持良好的性能。
简单的实现
  • 2-3树：相比其他复杂的自平衡树（如红黑树），2-3树的实现较为简单，容易理解和实现。
广泛的应用场景
  • 2-3树：适用于多种应用场景，如文件系统目录管理、字典编码、网络路由表等，展示了其在实际应用中的强大功能。
数据一致性
  • 2-3树：通过分裂和合并操作来维护数据的一致性，确保了在并发操作下的数据完整性。

综上所述，2-3树以其自平衡特性、灵活的节点结构、高效的性能、简单的实现以及广泛的应用场景，在许多实际应用中表现出色。选择2-3树作为数据结构可以带来诸多好处，特别是在需要高效操作和数据一致性的场景下。


http://www.kler.cn/a/325773.html

相关文章：

  • CC工具箱使用指南：【CAD导出界址点Excel】
  • JWT 过期后 自动刷新方案
  • ([LeetCode仓颉解题报告] 661. 图片平滑器
  • Ajax的相关内容
  • C语言项⽬实践-贪吃蛇
  • 矩阵的对角化特征值分解
  • JAVA开源项目 新闻推荐系统 计算机毕业设计
  • Flink 本地 idea 调试开启 WebUI
  • 【高分系列卫星简介——高分五号卫星（GF-5）】
  • 【Go语言基础——一个Go语言项目典型的文件结构示例】
  • 扩散模型DDPM代码实践
  • 黑马头条day7-app端文章搜索
  • Python语言中的重要函数对象用法
  • 【分布式微服务云原生】8分钟探索RPC：远程过程调用的奥秘与技术实现
  • 资质申请中常见的错误有哪些？
  • C++之设计模式
  • 商标名称注册查询，到底是查询什么！
  • 云计算Openstack
  • 全局异常处理与数据绑定：深入理解Spring的@ControllerAdvice
  • Oracle可编辑视图
  • 0基础学习QT——配置开发环境
  • 国内旅游：现状与未来趋势分析
  • 二、鼠标的解锁与锁定
  • ubuntu18.04安装教程
  • CSS-Day2
  • 技术成神之路：设计模式（十六）代理模式