《征服数据结构》哈夫曼树(Huffman Tree)
摘要:
1,哈夫曼树的介绍
2,哈夫曼树的构造
3,哈夫曼树带权路径长度计算
4,哈夫曼树的编码
5,哈夫曼树的解码
1,哈夫曼树的介绍
哈夫曼树(Huffman Tree)也叫霍夫曼树,或者赫夫曼树,又称为最优树,是因为它是一种带权路径长度最短的二叉树。在学习哈夫曼树之前我们先来了解一些和哈夫曼树相关的概念:
路径:从任一个节点往下到达其它节点之间的通路。
路径长度:路径中线段的个数。
节点的权:节点的值。
节点的带权路径长度:从根节点到该节点之间的路径长度与该节点权的乘积。
树的带权路径长度:所有叶子节点的带权路径长度之和。
在讲解哈夫曼树之前我们来看这样一个问题,假如老师根据学生的成绩给学生进行评级,有下面几个等级:
String level(int score) {
if (score < 60) return "不及格";
else if (score < 70) return "及格";
else if (score < 80) return "中等";
else if (score < 90) return "良好";
else return "优秀";
}上面的分支语句整理出来像一棵二叉树,如下图所示:
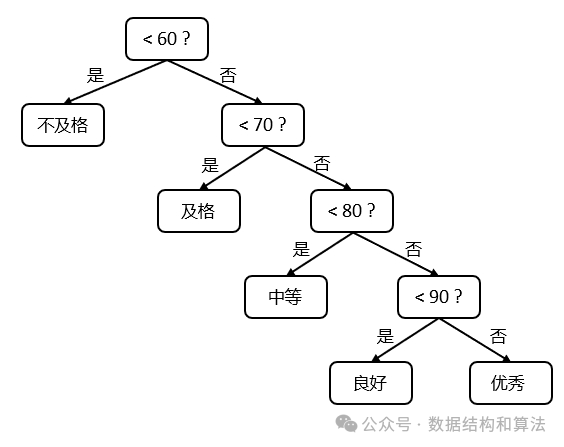
假如同学的成绩分布如下:
90分以上:10%
80到90分:35%
70到80分:45%
60到70分:8%
60分以下:2%可以看到60分以下的只有2%,但我们每次都是先判断是否小于60,很明显大多数情况下都不小于60,也就是无效的判断。
为了减少判断次数,最有效的判断方式就是占比越高的离根节点越近。可以看到分数在70到80分的占到45%,80到90分的占到35%,这两个加起来占了80%,这种情况下可以像下图中这样查询。
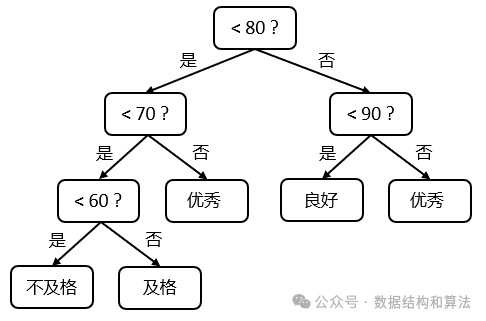
假如把这里的百分比看作叶子节点的权值,用它构造一棵二叉树,这棵二叉树可以有多种,其中带权路径长度最小的就是最优树,也是哈夫曼树。
哈夫曼树就是给定 n 个权值作为叶子节点,构造一棵二叉树,并且该树的带权路径长度达到最小。
树的带权路径长度 WPL(Weighted Path Length of Tree) 记为 WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln) ,其中 W 表示节点的权值, L 表示从根节点到该节点的路径长度。
要想让树的带权路径长度最小,权值越大的节点离根节点越近。如下图所示,是用权值为 9,3,2,8 分别构造的两棵树,很明显左边树的带权路径长度比右边树的带权路径长度要小。
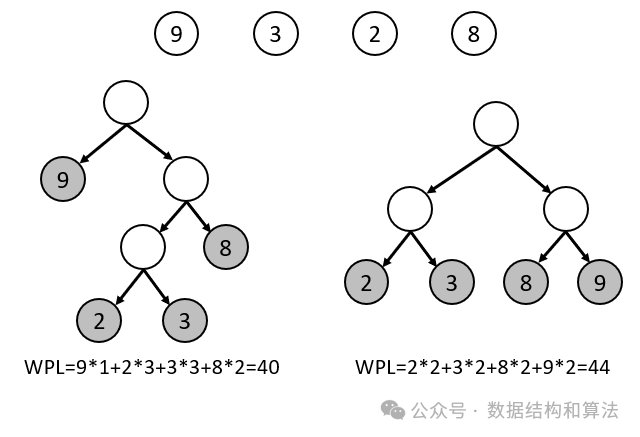
2,哈夫曼树的构造
哈夫曼树构造的原则是权值越大离根节点越近,使用的是贪心算法,步骤如下:
1. 用给定的 n 个权值创建 n 棵只有一个节点的树,把它们添加到集合 S 中。
2. 每次从集合 S 中取出两个权值最小的树,让它们组成一棵新的二叉树,新树的权值为它的两棵子树的权值之和,然后把这棵新的树添加到集合 S 中。
3. 重复步骤 2 ,直到集合中只有一棵树为止,这棵树就是哈夫曼树。
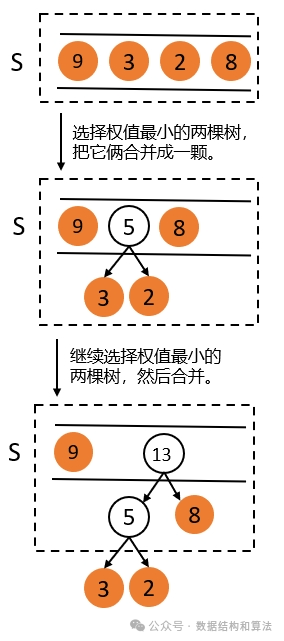
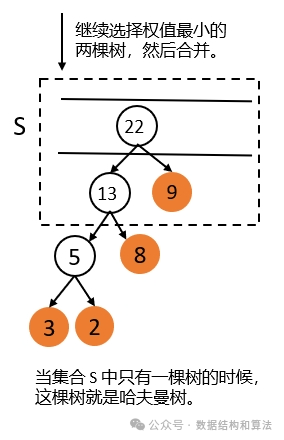
如上图所示,因为每次都是选择两棵子树合并成一棵,所以哈夫曼树只有度为 0 和 2 的节点,没有度为 1 的节点,也就是说哈夫曼树中每个节点要么没有子节点,要么有两个子节点,不可能只有一个子节点。
在二叉树中,度为 2 的节点贡献两条边,度为 1 的节点贡献一条边,度为 0 的节点不贡献任何边。在二叉树中除了根节点外,每一个节点都有一个父节点指向它,所以在任何二叉树中节点的数量等于边的数量加 1 。
假如哈夫曼树中,度为 0 (叶子节点)的节点有 n 个,度为 2 的节点有 m 个,我们可以得出边的数量是 2m ,总的节点是 m+n,根据 m+n=2m+1,可以得出 m=n-1,总的节点数就是 2n-1,所以我们可以得出一棵有 n 个叶子节点的哈夫曼树总共有 2n-1 个节点。
每次从集合中取出权值最小的两棵树,这里的集合我们可以使用最小堆,来看下代码。
Java 代码:
// 哈夫曼树的节点类。
public class HNode {
// 节点对应的字符,只有叶子节点有,在编码和解码的时候会用到。
private Character ch;
private int weight;// 权值。
private HNode left;// 左子树。
private HNode right;// 右子树。
private int deep;// 路径长度,也是节点的深度。
public HNode(int weight) {
this.weight = weight;
}
public HNode(HNode left, HNode right, int weight) {
this.left = left;
this.right = right;
this.weight = weight;
}
}
// 构建哈夫曼树
public HNode createTree(int[] nums) {
// 优先队列,这里使用最小堆
PriorityQueue<HNode> pq = new PriorityQueue<>(Comparator.comparingInt(o -> o.weight));
// 用数字创建只有一个节点的树并全部添加到堆中。
for (int num : nums)
pq.offer(new HNode(num));
while (pq.size() > 1) {// 大于 1 就合并。
HNode left = pq.poll();// 出队。
HNode right = pq.poll();
// 两棵子树合并成一棵。
HNode parent = new HNode(left, right, left.weight + right.weight);
// 把合并之后的子树添加到队列中。
pq.add(parent);
}
return pq.poll();// 最后一个就是构造成的哈夫曼树。
}C++ 代码:
struct HNode {// 哈夫曼树的节点类。
// 节点对应的字符,只有叶子节点有,在编码和解码的时候会用到。
char ch;
int weight = 0;// 权值。
HNode *left = nullptr;// 左子树。
HNode *right = nullptr;// 右子树。
int deep = 0;// 路径长度,也是节点的深度。
HNode(int weight) : weight(weight) {}
HNode(HNode *left, HNode *right, int weight) : left(left), right(right), weight(weight) {}
};
// 构建哈夫曼树
HNode *createTree(vector<int> &nums) {
auto cmp = [](HNode *a, HNode *b) { return a->weight > b->weight; };
// 优先队列,这里使用最小堆
priority_queue<HNode *, vector<HNode *>, decltype(cmp)> pq(cmp);
// 创建节点并全部添加到堆中。
for (int num: nums)
pq.push(new HNode(num));
while (pq.size() > 1) {// 大于 1 就合并。
HNode *left = pq.top();
pq.pop();// 出队。
HNode *right = pq.top();
pq.pop();// 出队。
// 两棵子树合并成一棵。
auto *parent = new HNode(left, right, left->weight + right->weight);
// 把合并之后的子树添加到队列中。
pq.push(parent);
}
return pq.top();// 最后一个就是构造成的哈夫曼树。
}3,哈夫曼树带权路径长度计算
