Kalman详尽原理介绍合集
目录
前言
1.线性kalman(LKF)
1.1LKF原理简介
1.2 适用场合
2.扩展kalman(EKF)
2.1LKF原理简介
2.2 适用场合
2.3 使用注意事项
3.无迹kalman(UKF)
3.1LKF原理简介
3.2 UT变换
3.3 适用场合
4.粒子滤波PF
4.1 PF原理简介
4.2 适用场合
前言
除了无模型控制和输出反馈的少部分系统,实际系统设计控制器时都是状态反馈,但是状态的获取往往是很困难的,这就需要利用量测量的信息,也就是传感器量测到的信息对状态变量进行估计,也就是我们所说的观测状态,对于目前主流的主要有扩张状态观测器、高增益观测器、Kalman滤波器,有的文章还会介绍扰动观测器等,但个人为扰动观测器和高增益观测器都可以归结为扩张状态观测器,扩张观测器又可以细分为线性扩张观测器LESO和非线性扩张观测器NLESO,对于LESO可以用高老师提出的宽带法调节,所有的观测器理论上可以无限还原名义模型。
对于往期也有部分文章介绍了扩张观测器:
基于扩张观测器(LESO)的滑模控制_Mr. 邹的博客-CSDN博客
VSC/SMC(八)——基于慢时变干扰观测器的滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客
VSC/SMC(七)——基于高增益观测器的滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客
自抗扰控制ADRC之扩张观测器_adrc扩张状态观测器_Mr. 邹的博客-CSDN博客
对于kalman的应用类型很多,可以做数据融合、参数辨识,本篇文章介绍其作为观测器上的应用,;kalman系列算法的基础都是贝叶斯滤波。
好了,本篇文章正式介绍Kalman这种类型的观测器,并且将其应用到2、4、7自由度悬架上进行仿真分析。
1.线性kalman(LKF)
1.1LKF原理简介
可以精简理解为:两步预测(状态和协方差阵)+两步更新(状态和协方差阵)+Klaman增益
![]()
![]()
![]()

![]()
由于kalman增益与预测和更新状态无直接关系,所以可以离线计算。
1.2 适用场合
①优点:计算迅速;程序稳定不容易崩溃
②缺点:适用于线性高斯模型;过程噪声和量测噪声局限于高斯白噪声。
2.扩展kalman(EKF)
2.1LKF原理简介
由于LKF局限于线性模型,所以提出EKF,可以精简理解为:将非线性模型进行一阶泰勒展开,其余算法部分仍与LKF一致,即两步预测、两步更新和离线Kalman增益计算。
一阶线性化即计算两个雅克比矩阵f()和h():
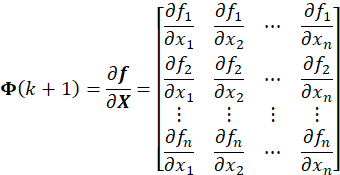

2.2 适用场合
①优点:不在使对象局限为线性模型;计算时间和LKF无差异,以及程序也很稳定
②缺点:需要人为事先计算好雅可比矩阵,即计算好泰勒一阶线性化模型;同样对于噪声只能是高斯白噪声;对于线性化后的模型还原真实的非线性模型差异很大,毕竟只能做到一阶线性化,从原理上可以理解为具有原系统的一阶精度,即存在线性化误差。
2.3 使用注意事项
对于建模时使用的是非线性模型(未经泰勒线性化模型),只是在作为滤波器时使用线性化模型。
3.无迹kalman(UKF)
3.1LKF原理简介
综述上述EKF线性化误差很大的原由本质在于用泰勒展开时只是离散化到一阶,所以这部分误差不可避免地存在,而且很大。
剖析Kalman的本质,可以知道就是在玩转概率分布和方差,所以引出无迹变换(UT)代替一阶泰勒线性化,UT变换的原理可以理解为用符合正态分布的sigma点近似原系统的概率密度函数,这样只需要计算sigma点的期望和方差便可以还原实际非线性系统的期望和方差,由于通过这种方法计算对于二阶系统期望和方差一致,所以可以理解为UKF具有至少二阶精度。有的资料上也会说对于高斯分布模型具有3阶以上精度,具体读者感兴趣可以推导。
对于具体的算法流程部分读者可以可以相关资料,暂时没时间补充,谢谢理解!
3.2 UT变换
UT变换是基于先验期望和协方差阵来得到的,一般将sigma点按对称分布选取。其实可以理解为选取sigma点位置和权重两个部分,其中权重是固定的,也可以理解为是可以离线计算的。

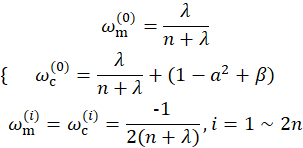
3.3 适用场合
①优点:相较于计算精度而言比LKF和EKF有很大的提升;不再局限于线性模型
②缺点:程序不稳定(由于需要LL'分解,所以协方差阵需要一直保证为正定阵,而软件的计算精度有限会导致丢失精度最终导致矩阵非正定);计算时间较长
4.粒子滤波PF
4.1 PF原理简介
由于计算期望和方差都需要∞积分,但是实际中不存在,就会导致无可行解的问题。PF提出的最大精髓在于利用大数定律的思想:将频率近似为概率,所以只要频率足够大,那么概率就足够准确。
对于算法流程部分,主要包括:重要性采样(即粒子初始位置的选择和初始权重选取)、重采样机制。很复杂这里就不去编辑叙述了,读者查阅相关资料阅读,谢谢理解!
4.2 适用场合
①优点:相较于LKF、EKF和UKF,它不再局限于白噪声,噪声可以是有色噪声,其期望不为0的噪声;精度最高,理论上只要粒子数量足够多,那么便能绝对还原非线性模型
②缺点:计算内存最大。
对于应用部分放到下篇文章进行仿真分析,敬请关注!
好了,以上便是个人对于LKF、EKF、UKF和PF的理解,如有错误欢迎指导交流!发文不易,如果有帮助请帮忙点个小爱心,谢谢!
