数据结构双向链表和循环链表
目录
- 一、循环链表
- 二、双向链表
- 三、循环双向链表
一、循环链表
循环链表就是首尾相接的的链表,就是尾节点的指针域指向头节点使整个链表形成一个循环,这就弥补了以前单链表无法在后面某个节点找到前面的节点,可以从任意一个节点找到目标节点,但是现在我们就不能像以前那样停止循环时的判断条件是否为NULL了,而是判断是否指向头指针


由于我们的操作经常是在链表的首位进行操作,所以我们引进尾指针的概念,这样以后就可以直接找到操作尾节点

下面是循环单链表的相关代码:
typedef struct
{
int data;
Lnode* next;
}*CirList,Lnode;
//初始化一个循环单链表
bool init_list(CirList& l)
{
l = new Lnode;//开辟空间作为头节点
if (l == NULL)return false;
l->next = l;//头指针的指针域指向自己
return true;
}
//判断循环单链表是否为空表
bool isEmpty(CirList& l)
{
if (l->next == l)return true;
return false;
}
二、双向链表
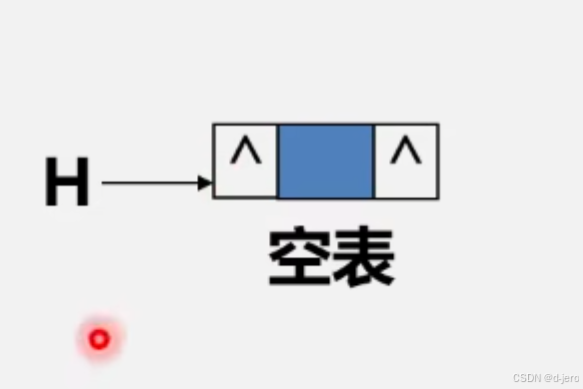
由于单链表无法逆向检索,循环链表逆向寻找元素时间复杂度也是O(n),所以这里提出双向链表的概念,就是给每个元素一个前驱指针,这样我们就可以直接逆向检索上一个元素了,而且时间复杂度为O(1);双向链表的空表里面两个指针装的都是空指针
#include<iostream>
using namespace std;
typedef struct Lnode
{
int data;
Lnode* next,*prior;
}*DoubList,Lnode;
//初始化一个双向链表
bool init_list(DoubList& l)
{
l = new Lnode;
if (l == NULL)return false;
l->next = NULL;
l->prior = NULL;
return true;
}
//双向链表建立(前插法)
bool insert_list(DoubList& l)
{
init_list(l);
int x;
while (cin >> x && x != 0)
{
Lnode* p = new Lnode{x,l->next,l};
if (p == NULL)return false;
if (l->next)l->next->prior = p;
l->next = p;
}
return true;
}
//双链表建立(后插法)
bool insert_tail_list(DoubList& l)
{
init_list(l);
int x;
Lnode* r =l;
while (cin >> x && x != 0)
{
Lnode* p = new Lnode{ x,NULL,r };
if (p == NULL)return false;
r->next = p;
r = p;
}
return true;
}
//按位插入:在i位插入元素e
bool insertElem(DoubList& l, int i, int e)
{
if (i < 1)return false;
int j=0;
Lnode* r = l;
while (j < i - 1 && r->next != NULL)
{
r = r->next;
j++;
}
if (j != i - 1)return false;
Lnode* p = new Lnode{ e,r->next,r };
if (r->next)r->next->prior = p;
r->next = p;
return true;
}
//按值删除元素e
void deleteElem(DoubList&l,int e)
{
if (!l->next)cout << "删除失败:链表为空" << endl;
Lnode* r = l->next;
while (r)
{
if (r->data == e)
{
r->prior->next = r->next;
if (r->next)r->next->prior = r->prior;
delete r;
r = NULL;
return;
}
r = r->next;
}
}
//打印双链表
void print(DoubList l)
{
Lnode* p=l;
while (p->next)
{
p = p->next;
cout << p->data << "\t";
}
cout << endl;
}
int main()
{
DoubList l;
insert_list(l);
print(l);
deleteElem(l, 3);
print(l);
return 0;
}
三、循环双向链表
即使我们有了双向链表,但是当我们想要在尾节点找到头节点附近某个节点仍然不够快捷,所以就引进了循环双向链表的概念,不过判断条件这些就需要改变:判断结束条件从NULL变为链表名L
#include<iostream>
using namespace std;
typedef struct Lnode
{
int data;
Lnode* next,*prior;
}*DoubCirList,Lnode;
//初始化一个循环双向链表
bool init_list(DoubCirList& l)
{
l = new Lnode;
if (l == NULL)return false;
//指针域都指向自身
l->next = l;
l->prior = l;
return true;
}
//双向循环链表建立(前插法)
bool insert_list(DoubCirList& l)
{
init_list(l);
int x;
while (cin >> x && x != 0)
{
Lnode* p = new Lnode{x,l->next,l};
if (p == NULL)return false;
l->next->prior = p;
l->next = p;
}
return true;
}
//双链表建立(后插法)
bool insert_tail_list(DoubCirList& l)
{
init_list(l);
int x;
Lnode* r =l;
while (cin >> x && x != 0)
{
Lnode* p = new Lnode{ x,l,r };
if (p == NULL)return false;
r->next = p;
r = p;
}
return true;
}
//按位插入:在i位插入元素e
bool insertElem(DoubCirList& l, int i, int e)
{
if (i < 1)return false;
int j=0;
Lnode* r = l;
while (j < i - 1 && r->next != l)
{
r = r->next;
j++;
}
if (j != i - 1)return false;
Lnode* p = new Lnode{ e,r->next,r };
r->next->prior = p;
r->next = p;
return true;
}
//按值删除元素e
void deleteElem(DoubCirList&l,int e)
{
if (l->next==l)cout << "删除失败:链表为空" << endl;
Lnode* r = l->next;
while (r!=l)
{
if (r->data == e)
{
r->next->prior = r->prior;
r->prior->next = r->next;
delete r;
r = NULL;
return;
}
r = r->next;
}
}
//打印双链表
void print(DoubCirList l)
{
Lnode* p=l;
while (p->next!=l)
{
p = p->next;
cout << p->data << "\t";
}
cout << endl;
}
int main()
{
DoubCirList l;
insert_tail_list(l);
print(l);
return 0;
}
