SCoRe: 通过强化学习教导大语言模型进行自我纠错
大语言模型(LLMs)在推理任务中,如数学问题求解和编程,已经展现出了优秀的性能。尽管它们能力强大,但在实现能够通过计算和交互来改进其回答的算法方面仍然面临挑战。现有的自我纠错方法要么依赖于提示工程,要么需要使用额外的模型进行微调,但这些方法都有局限性,往往无法产生有意义的自我纠错。
这是谷歌9月发布在arxiv上的论文,研究者们提出了一种新方法自我纠错强化学习(SCoRe),旨在使大语言模型能够在没有任何外部反馈或评判的情况下"即时"纠正自己的错误。SCoRe通过在线多轮强化学习,使用自生成的数据来训练单一模型。这种方法解决了监督式微调中的一些挑战,如模型倾向于进行微小编辑而不做实质性改进,以及训练数据与推理数据之间分布差异所带来的问题。
方法详细描述
SCoRe的工作原理分为两个阶段:
- 初始化阶段:- 训练模型优化纠错性能,同时保持其初始回答接近基础模型的回答。- 这可以防止模型在第一次尝试时偏离太远。
- 强化学习阶段:- 模型进行多轮强化学习,以最大化初始回答和纠正后回答的奖励。- 包含一个奖励加成,以鼓励从第一次到第二次尝试有显著改进。
通过这种训练结构,SCoRe确保模型不仅仅是产生最佳的初始回答并进行最小化纠正,而是学会对其初始答案进行有意义的改进。
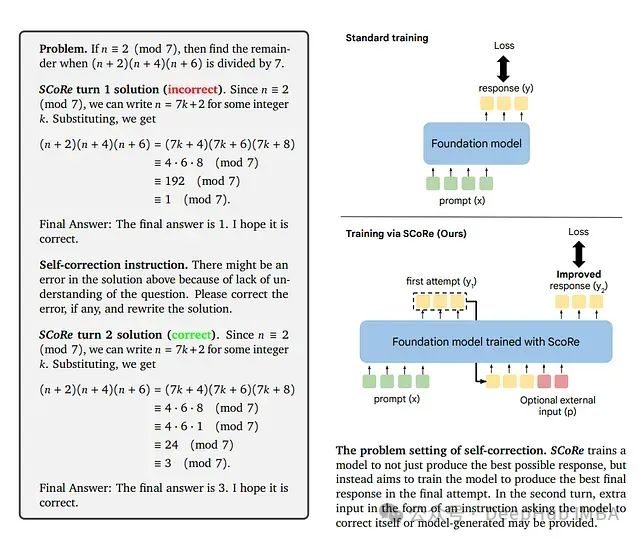
如图所示,SCoRe的方法概述包括了初始化阶段和强化学习阶段,展示了如何通过这两个阶段来优化模型的自我纠错能力。
改进指标介绍
实验结果表明,SCoRe显著提高了大语言模型的内在自我纠错能力。研究者们使用了以下指标来评估模型的性能:
- Accuracy@t1: 模型在第一次尝试时的准确率
- Accuracy@t2: 模型在第二次尝试时的准确率
- Δ(t1, t2): 模型在第一次和第二次尝试之间准确率的净改善,衡量了自我纠错的有效性
- Δi→c(t1, t2): 在第一次尝试中错误但在第二次尝试中变正确的问题比例,衡量了自我纠错能解决多少新问题
- Δc→i(t1, t2): 在第一次尝试中正确但在第二次尝试中变错误的问题比例,衡量了模型对什么使回答正确的理解程度
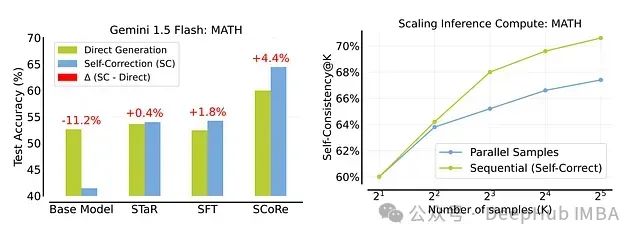
如图所示,SCoRe在这些指标上相比基准模型和其他方法都取得了显著的改进。
实验结果与方法比较
基准任务
研究者们在两个代表性的推理任务上进行了实验,这些任务中错误纠正至关重要:
- 数学问题求解:使用MATH数据集(Hendrycks et al., 2021)
- 代码生成:使用MBPP(Austin et al., 2021)和HumanEval(Chen et al., 2021)数据集
MATH数据集结果
在MATH数据集上,SCoRe展现出了显著的性能提升:
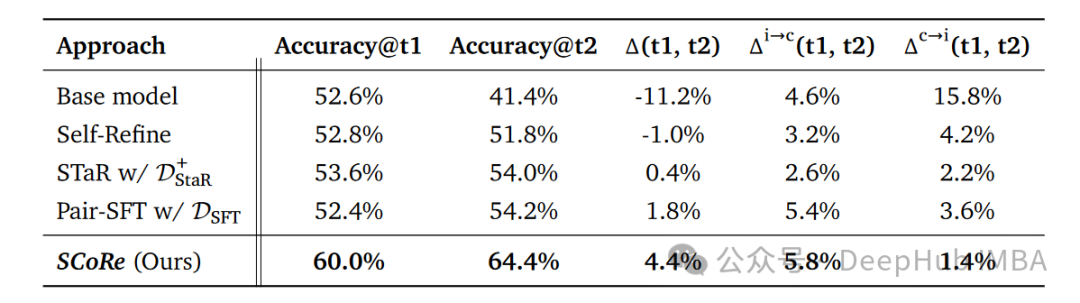
SCoRe不仅在两次尝试中都达到了更高的准确率,还提供了最积极的自我纠错性能Δ(t1, t2)。它提高了从错误到正确的问题数量,同时大幅减少了从正确变为错误的问题数量。
代码生成任务结果
在代码生成任务上,SCoRe同样展现出了强大的性能:
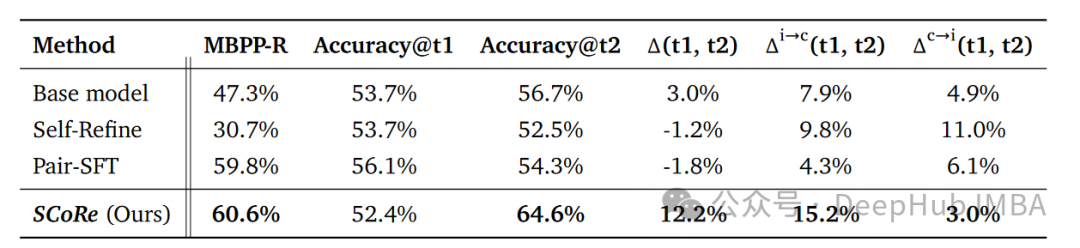
SCoRe在HumanEval上实现了12.2%的内在自我纠错增益,比基础模型高出9%。在MBPP-R(一个离线修复任务)上,SCoRe将基础模型的性能从47.3%提升到60.6%,这个差距相当于GPT-3.5和GPT-4之间的差距。
与其他方法的比较
- Self-Refine:这是一种基于提示的方法,旨在引出模型的自我纠错行为。然而,在没有外部输入的情况下,它难以实现有效的内在自我纠错。
- Pair-SFT:这种方法基于Welleck等人(2023)的工作,在合成配对的修复轨迹上进行监督微调。虽然在静态修复任务MBPP-R上表现不错,但在自我纠错设置中实际上降低了基础模型的性能。
- STaR:这种方法在成功的修复轨迹上进行监督微调。虽然它在某些情况下可以改善性能,但仍然无法达到SCoRe的水平。
SCoRe的优势在于它通过在线多轮强化学习来训练模型,使用完全自生成的数据。这使得模型能够在没有任何外部反馈或评判的情况下学习有效的自我纠错策略。
推理计算扩展性
研究者们还调查了SCoRe是否可以与推理时计算扩展策略结合使用。他们评估了自洽解码(Wang et al., 2022),也称为多数投票,其中采样多样化的解决方案集,然后选择这些解决方案中最一致的答案。
如图1所示(第一张图),研究者们发现,与其并行采样2K个解决方案,不如并行采样K个解决方案,然后对每个解决方案进行一轮自我纠错。在每个问题32个解决方案的预算下,并行采样显示7.4%的准确率增益,而结合顺序采样的自我纠错产生10.5%的改进。
这一结果表明,SCoRe不仅能提高模型的自我纠错能力,还能有效地与其他推理优化技术结合,进一步提升模型性能。
讨论、局限性
讨论
SCoRe方法在为大语言模型注入自我纠错能力方面取得了显著的成功。研究者们通过广泛的评估证明,SCoRe是第一个能够实现显著正面内在自我纠错性能的方法。为了解释SCoRe的设计原理,研究者们严格分析了各种微调基线的行为,并确定了在这些方法下模型学习非纠错策略(例如,学习不进行编辑)的失败模式。
SCoRe的设计旨在通过利用两阶段结构和奖励塑造来引导出自我纠错策略,这两个特性都有助于防止模型崩溃为不学习有效的自我改进行为。这种方法的成功表明,学习元策略(如本文中的自我纠错)可能需要超越标准的监督微调范式,后者通常由单轮强化学习(RL)跟随。
局限性
尽管SCoRe取得了显著的成果,但研究者们也指出了一些局限性:
- 迭代次数限制:在本研究中,SCoRe仅训练了一轮迭代自我纠错,这意味着后续的纠错轮次可能不如第一轮有效。
- 计算成本:SCoRe的两阶段训练过程可能比单一阶段的方法需要更多的计算资源。
- 奖励函数设计:虽然SCoRe使用了简单的奖励函数,但设计更复杂、更有效的奖励函数可能会进一步提高性能。
- 泛化能力:虽然SCoRe在测试集上表现良好,但在更广泛的、可能未见过的任务上的泛化能力还需要进一步研究。
未来研究方向
基于这些局限性,研究者们提出了几个潜在的未来研究方向:
- 多轮迭代训练:通过RL训练更多轮次的自我纠错,这已经是使用监督微调(SFT)获得有效自我纠错行为超过两轮的常见和有效做法。
- 统一SCoRe的两个阶段:研究如何将SCoRe的初始化阶段和强化学习阶段统一起来,这可能会缓解运行多个步骤的限制,并有助于设计更强大的方法。
- 细粒度反馈:在生成多轮RL的策略路径时使用更详细或更细粒度的监督可能会进一步提高模型实现复杂策略的能力。
- 探索其他任务:将SCoRe应用于更广泛的任务,如自然语言生成、对话系统等,以测试其泛化能力。
总结
SCoRe代表了大语言模型自我纠错能力研究的重要进展。通过创新的两阶段强化学习方法,SCoRe成功地教会了模型如何识别和纠正自己的错误,而无需任何外部反馈。这项研究不仅提高了模型的性能,还为理解和改进AI系统的自我改进能力提供了宝贵的见解。
研究结果表明,SCoRe在数学推理和代码生成等任务中显著优于现有方法,展示了其在提高大语言模型自我纠错能力方面的潜力。这项工作为未来的研究开辟了新的道路,特别是在探索如何使AI系统更加自主和适应性强方面。
总的来说,SCoRe的成功凸显了在大语言模型训练中采用更复杂的学习策略的重要性,尤其是当目标是培养高级认知能力如自我纠错时。随着这一领域的不断发展,我们可以期待看到更多创新方法的出现,进一步推动AI系统的能力界限。
https://avoid.overfit.cn/post/84d1cd5034a94a7bb51dfbe951b30ed2
