当前位置： 首页 > article >正文

堆Heap

article 2025/1/7 5:47:57

堆（heap）是一种满足特定条件的完全二叉树，主要可分为两种类型，如图 8-1 所示。

  • 小顶堆（min heap）：任意节点的值 ≤ 其子节点的值。
  • 大顶堆（max heap）：任意节点的值 ≥ 其子节点的值。

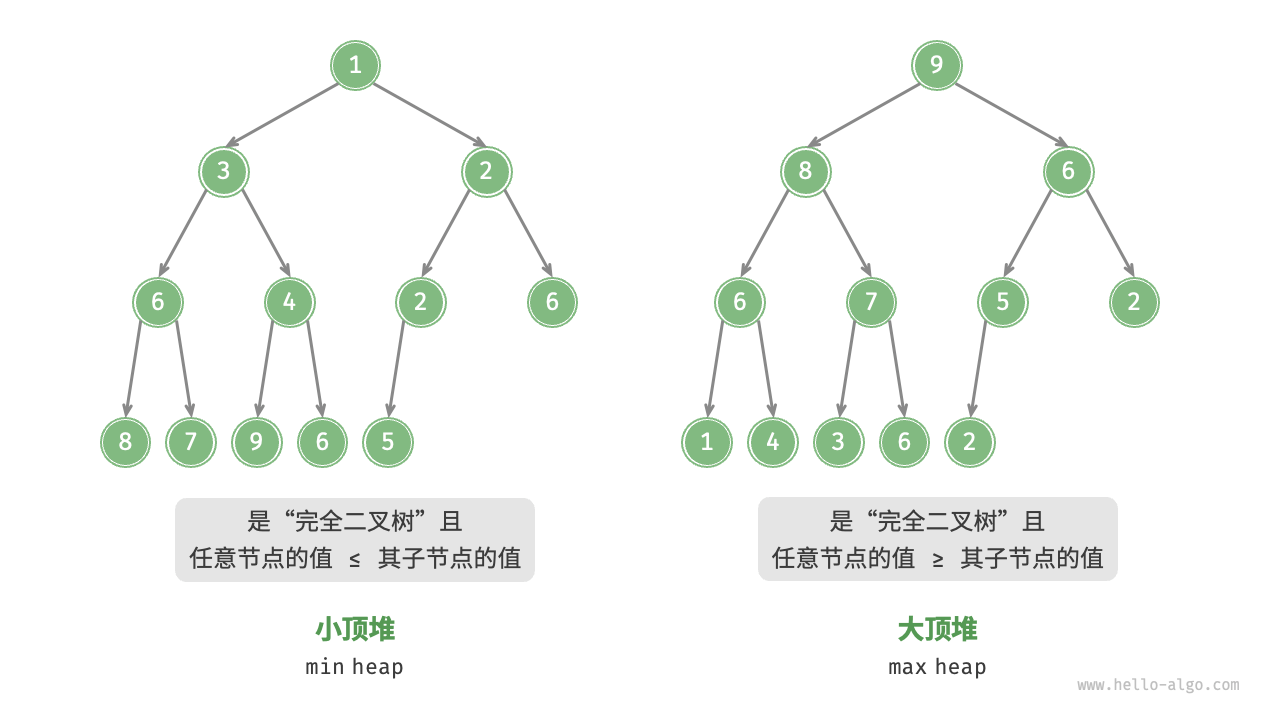
图 8-1 小顶堆与大顶堆

堆作为完全二叉树的一个特例，具有以下特性。

  • 最底层节点靠左填充，其他层的节点都被填满。
  • 我们将二叉树的根节点称为“堆顶”，将底层最靠右的节点称为“堆底”。
  • 对于大顶堆（小顶堆），堆顶元素（根节点）的值是最大（最小）的。

8.1.1 堆的常用操作

需要指出的是，许多编程语言提供的是优先队列（priority queue），这是一种抽象的数据结构，定义为具有优先级排序的队列。

实际上，堆通常用于实现优先队列，大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看，我们可以将“优先队列”和“堆”看作等价的数据结构。因此，本书对两者不做特别区分，统一称作“堆”。

堆的常用操作见表 8-1 ，方法名需要根据编程语言来确定。

表 8-1 堆的操作效率

方法名

描述

时间复杂度

push()

元素入堆

O(log⁡n)

pop()

堆顶元素出堆

O(log⁡n)

peek()

访问堆顶元素（对于大 / 小顶堆分别为最大 / 小值）

O(1)

size()

获取堆的元素数量

O(1)

isEmpty()

判断堆是否为空

O(1)

在实际应用中，我们可以直接使用编程语言提供的堆类（或优先队列类）。

类似于排序算法中的“从小到大排列”和“从大到小排列”，我们可以通过设置一个 flag 或修改 Comparator 实现“小顶堆”与“大顶堆”之间的转换。代码如下所示：

/* 初始化堆 */
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大顶堆
priority_queue<int, vector<int>, less<int>> maxHeap;

/* 元素入堆 */
maxHeap.push(1);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(5);
maxHeap.push(4);

/* 获取堆顶元素 */
int peek = maxHeap.top(); // 5

/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
maxHeap.pop(); // 5
maxHeap.pop(); // 4
maxHeap.pop(); // 3
maxHeap.pop(); // 2
maxHeap.pop(); // 1

/* 获取堆大小 */
int size = maxHeap.size();

/* 判断堆是否为空 */
bool isEmpty = maxHeap.empty();

/* 输入列表并建堆 */
vector<int> input{1, 3, 2, 5, 4};
priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());

8.1.2 堆的实现

下文实现的是大顶堆。若要将其转换为小顶堆，只需将所有大小逻辑判断进行逆转（例如，将 ≥ 替换为 ≤ ）。感兴趣的读者可以自行实现。

1. 堆的存储与表示

“二叉树”章节讲过，完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树，因此我们将采用数组来存储堆。

当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。

如图 8-2 所示，给定索引 i ，其左子节点的索引为 2i+1 ，右子节点的索引为 2i+2 ，父节点的索引为 (i−1)/2（向下整除）。当索引越界时，表示空节点或节点不存在。

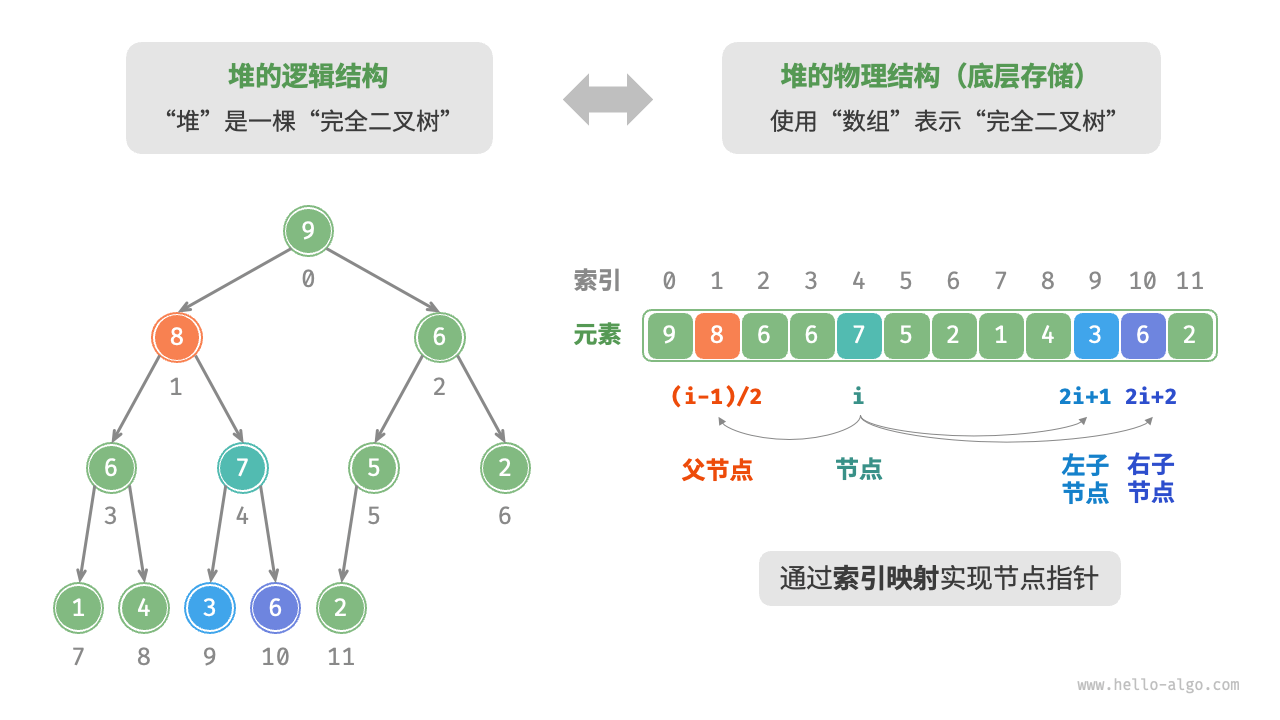
图 8-2 堆的表示与存储

我们可以将索引映射公式封装成函数，方便后续使用：

/* 获取左子节点的索引 */
int left(int i) {
    return 2 * i + 1;
}

/* 获取右子节点的索引 */
int right(int i) {
    return 2 * i + 2;
}

/* 获取父节点的索引 */
int parent(int i) {
    return (i - 1) / 2; // 向下整除
}

2. 访问堆顶元素

堆顶元素即为二叉树的根节点，也就是列表的首个元素：

/* 访问堆顶元素 */
int peek() {
    return maxHeap[0];
}

3. 元素入堆

给定元素 val ，我们首先将其添加到堆底。添加之后，由于 val 可能大于堆中其他元素，堆的成立条件可能已被破坏，因此需要修复从插入节点到根节点的路径上的各个节点，这个操作被称为堆化（heapify）。

考虑从入堆节点开始，从底至顶执行堆化。如图 8-3 所示，我们比较插入节点与其父节点的值，如果插入节点更大，则将它们交换。然后继续执行此操作，从底至顶修复堆中的各个节点，直至越过根节点或遇到无须交换的节点时结束。

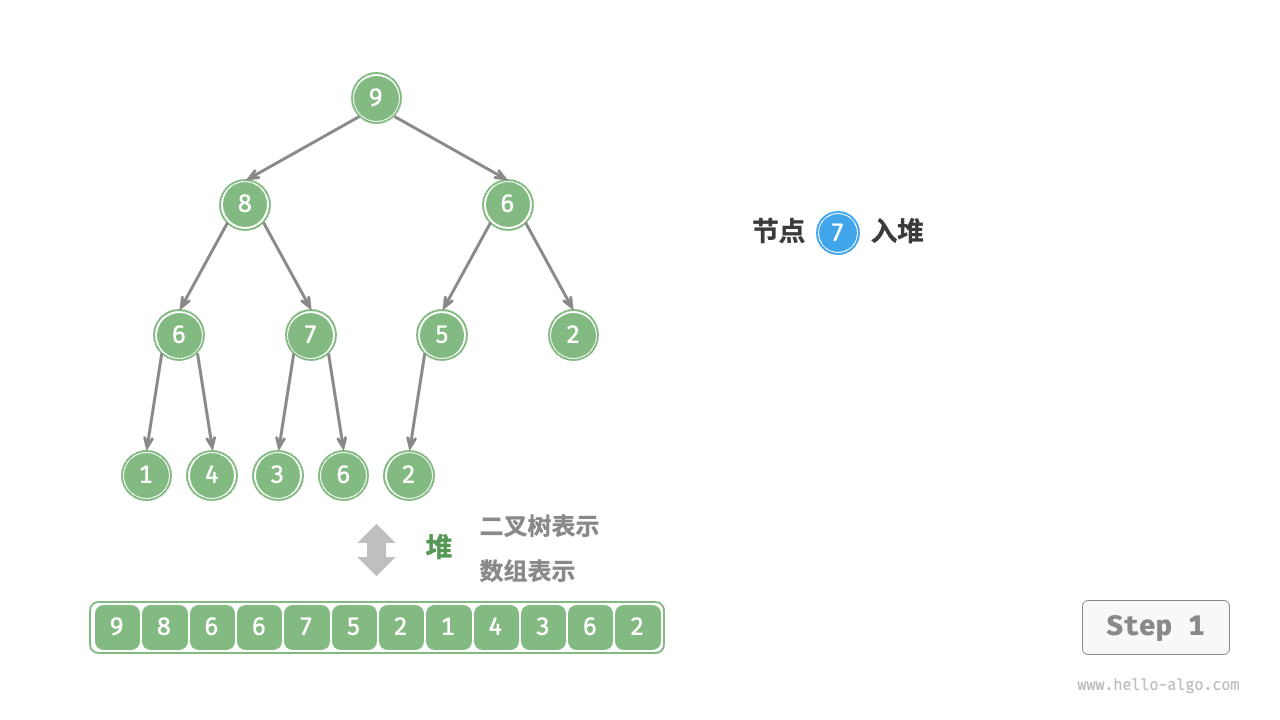
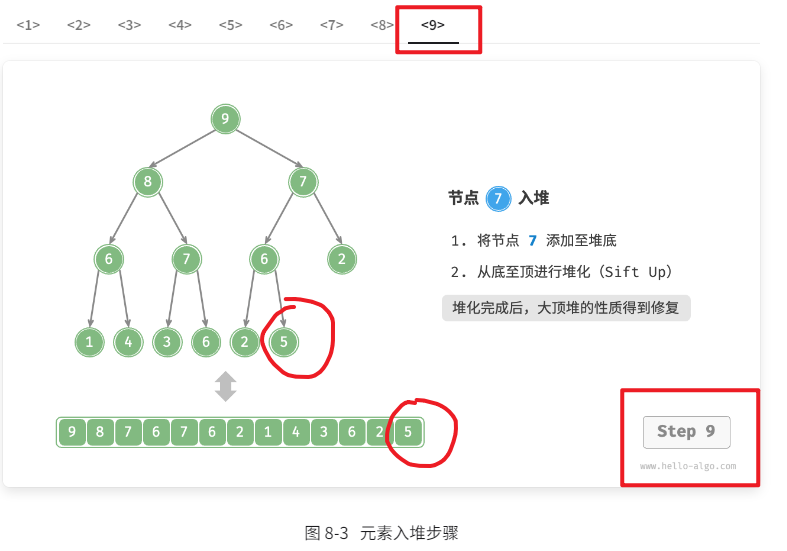
图 8-3 元素入堆步骤

设节点总数为 n ，则树的高度为 O(log⁡n) 。由此可知，堆化操作的循环轮数最多为 O(log⁡n) ，元素入堆操作的时间复杂度为 O(log⁡n) 。代码如下所示：

/* 元素入堆 */
void push(int val) {
    // 添加节点
    maxHeap.push_back(val);
    // 从底至顶堆化
    siftUp(size() - 1);
}

/* 从节点 i 开始，从底至顶堆化 */
void siftUp(int i) {
    while (true) {
        // 获取节点 i 的父节点
        int p = parent(i);
        // 当“越过根节点”或“节点无须修复”时，结束堆化
        if (p < 0 || maxHeap[i] <= maxHeap[p])
            break;
        // 交换两节点
        swap(maxHeap[i], maxHeap[p]);
        // 循环向上堆化
        i = p;
    }
}

4. 堆顶元素出堆

堆顶元素是二叉树的根节点，即列表首元素。如果我们直接从列表中删除首元素，那么二叉树中所有节点的索引都会发生变化，这将使得后续使用堆化进行修复变得困难。为了尽量减少元素索引的变动，我们采用以下操作步骤。

  1. 交换堆顶元素与堆底元素（交换根节点与最右叶节点）。
  2. 交换完成后，将堆底从列表中删除（注意，由于已经交换，因此实际上删除的是原来的堆顶元素）。
  3. 从根节点开始，从顶至底执行堆化。

如图 8-4 所示，“从顶至底堆化”的操作方向与“从底至顶堆化”相反，我们将根节点的值与其两个子节点的值进行比较，将最大的子节点与根节点交换。然后循环执行此操作，直到越过叶节点或遇到无须交换的节点时结束。

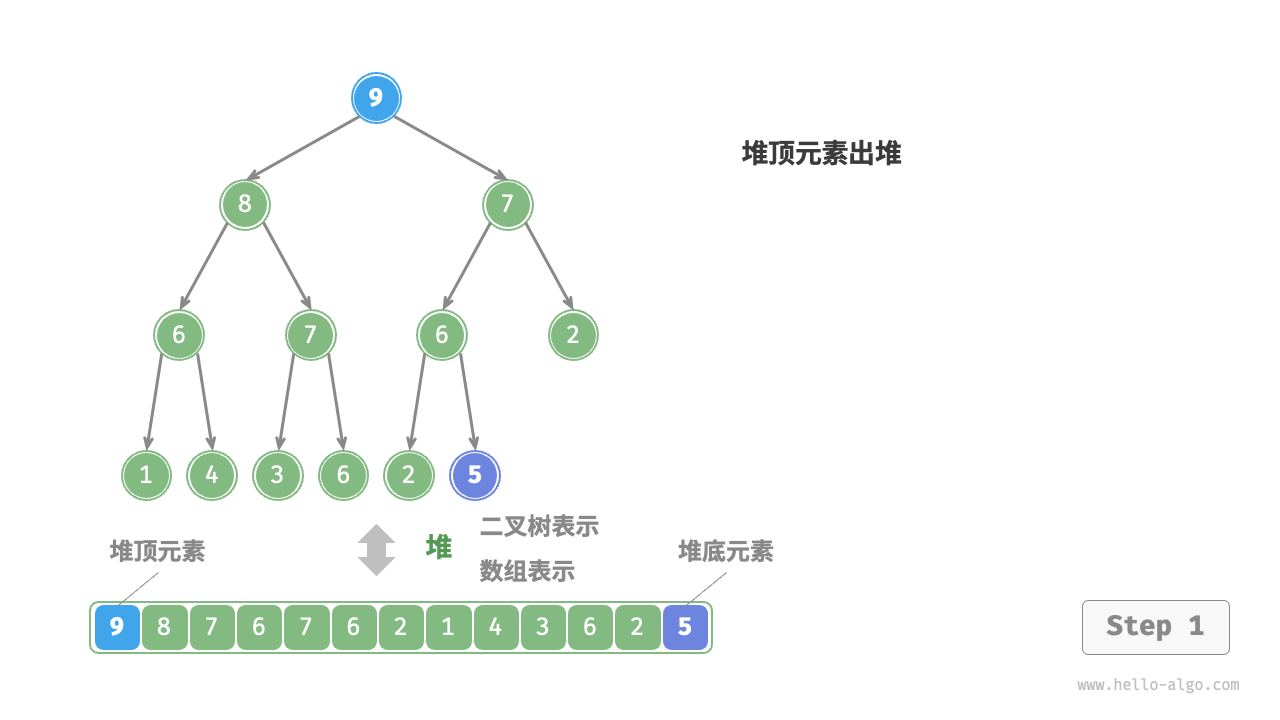
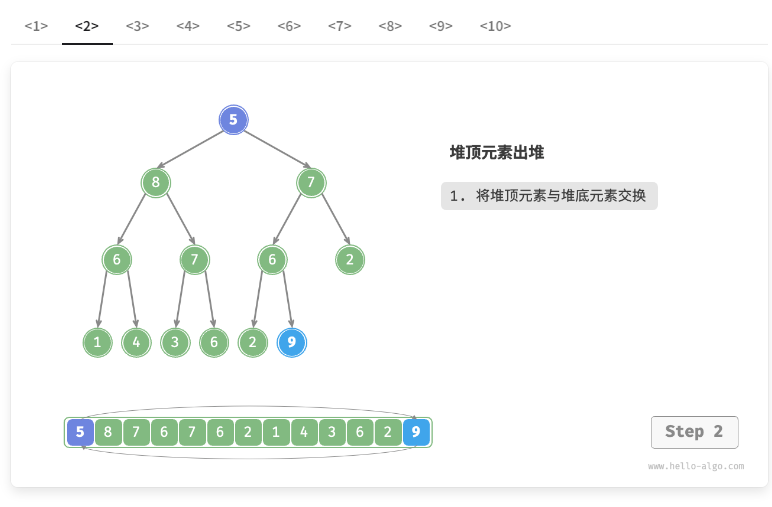
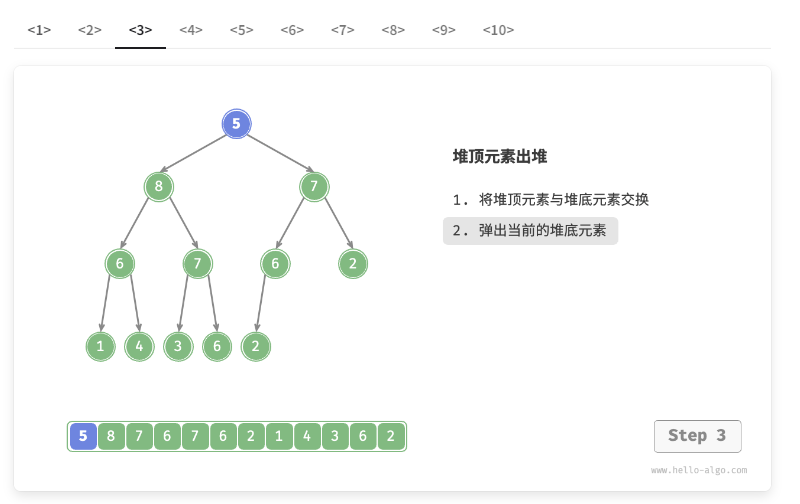
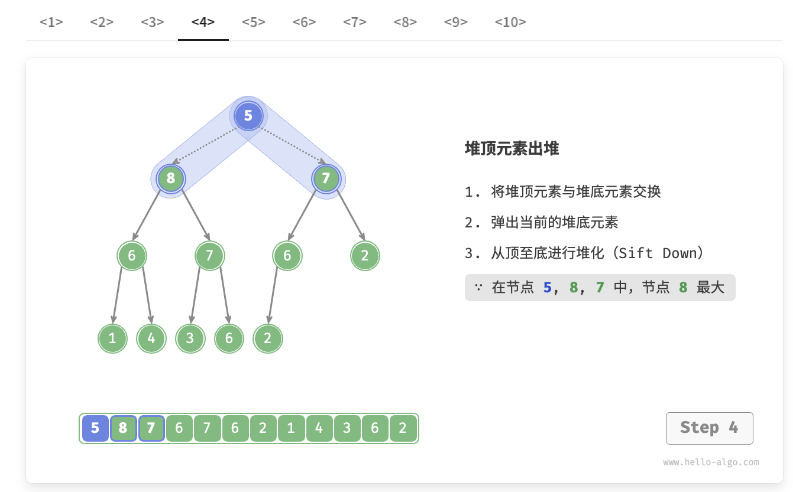
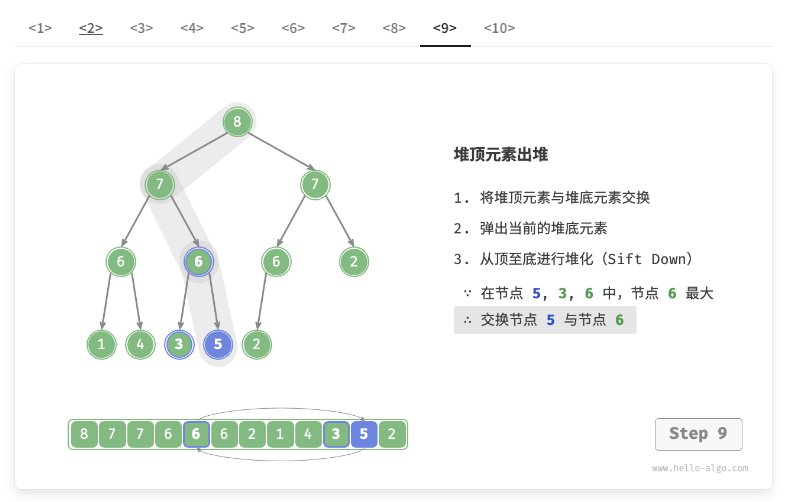
图 8-4 堆顶元素出堆步骤

与元素入堆操作相似，堆顶元素出堆操作的时间复杂度也为 O(log⁡n) 。代码如下所示：

/* 元素出堆 */
void pop() {
    // 判空处理
    if (isEmpty()) {
        throw out_of_range("堆为空");
    }
    // 交换根节点与最右叶节点（交换首元素与尾元素）
    swap(maxHeap[0], maxHeap[size() - 1]);
    // 删除节点
    maxHeap.pop_back();
    // 从顶至底堆化
    siftDown(0);
}

/* 从节点 i 开始，从顶至底堆化 */
void siftDown(int i) {
    while (true) {
        // 判断节点 i, l, r 中值最大的节点，记为 ma
        int l = left(i), r = right(i), ma = i;
        if (l < size() && maxHeap[l] > maxHeap[ma])
            ma = l;
        if (r < size() && maxHeap[r] > maxHeap[ma])
            ma = r;
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if (ma == i)
            break;
        swap(maxHeap[i], maxHeap[ma]);
        // 循环向下堆化
        i = ma;
    }
}

8.1.3 堆的常见应用

  • 优先队列：堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为 O(log⁡n) ，而建堆操作为 O(n) ，这些操作都非常高效。
  • 堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。然而，我们通常会使用一种更优雅的方式实现堆排序，详见“堆排序”章节。
  • 获取最大的 k 个元素：这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

8.2 建堆操作

在某些情况下，我们希望使用一个列表的所有元素来构建一个堆，这个过程被称为“建堆操作”。

8.2.1 借助入堆操作实现

我们首先创建一个空堆，然后遍历列表，依次对每个元素执行“入堆操作”，即先将元素添加至堆的尾部，再对该元素执行“从底至顶”堆化。

每当一个元素入堆，堆的长度就加一。由于节点是从顶到底依次被添加进二叉树的，因此堆是“自上而下”构建的。

设元素数量为 n ，每个元素的入堆操作使用 O(log⁡n) 时间，因此该建堆方法的时间复杂度为 O(nlog⁡n) 。

8.2.2 通过遍历堆化实现

实际上，我们可以实现一种更为高效的建堆方法，共分为两步。

  1. 将列表所有元素原封不动地添加到堆中，此时堆的性质尚未得到满足。
  2. 倒序遍历堆（层序遍历的倒序），依次对每个非叶节点执行“从顶至底堆化”。

每当堆化一个节点后，以该节点为根节点的子树就形成一个合法的子堆。而由于是倒序遍历，因此堆是“自下而上”构建的。

之所以选择倒序遍历，是因为这样能够保证当前节点之下的子树已经是合法的子堆，这样堆化当前节点才是有效的。

值得说明的是，由于叶节点没有子节点，因此它们天然就是合法的子堆，无须堆化。如以下代码所示，最后一个非叶节点是最后一个节点的父节点，我们从它开始倒序遍历并执行堆化：

/* 构造方法，根据输入列表建堆 */
MaxHeap(vector<int> nums) {
    // 将列表元素原封不动添加进堆
    maxHeap = nums;
    // 堆化除叶节点以外的其他所有节点
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}

可视化运行

8.2.3 复杂度分析

下面，我们来尝试推算第二种建堆方法的时间复杂度。

  • 假设完全二叉树的节点数量为 n ，则叶节点数量为 (n+1)/2 ，其中 / 为向下整除。因此需要堆化的节点数量为 (n−1)/2 。
  • 在从顶至底堆化的过程中，每个节点最多堆化到叶节点，因此最大迭代次数为二叉树高度 log⁡n 。

将上述两者相乘，可得到建堆过程的时间复杂度为 O(nlog⁡n) 。但这个估算结果并不准确，因为我们没有考虑到二叉树底层节点数量远多于顶层节点的性质。

接下来我们来进行更为准确的计算。为了降低计算难度，假设给定一个节点数量为 n 、高度为 h 的“完美二叉树”，该假设不会影响计算结果的正确性。

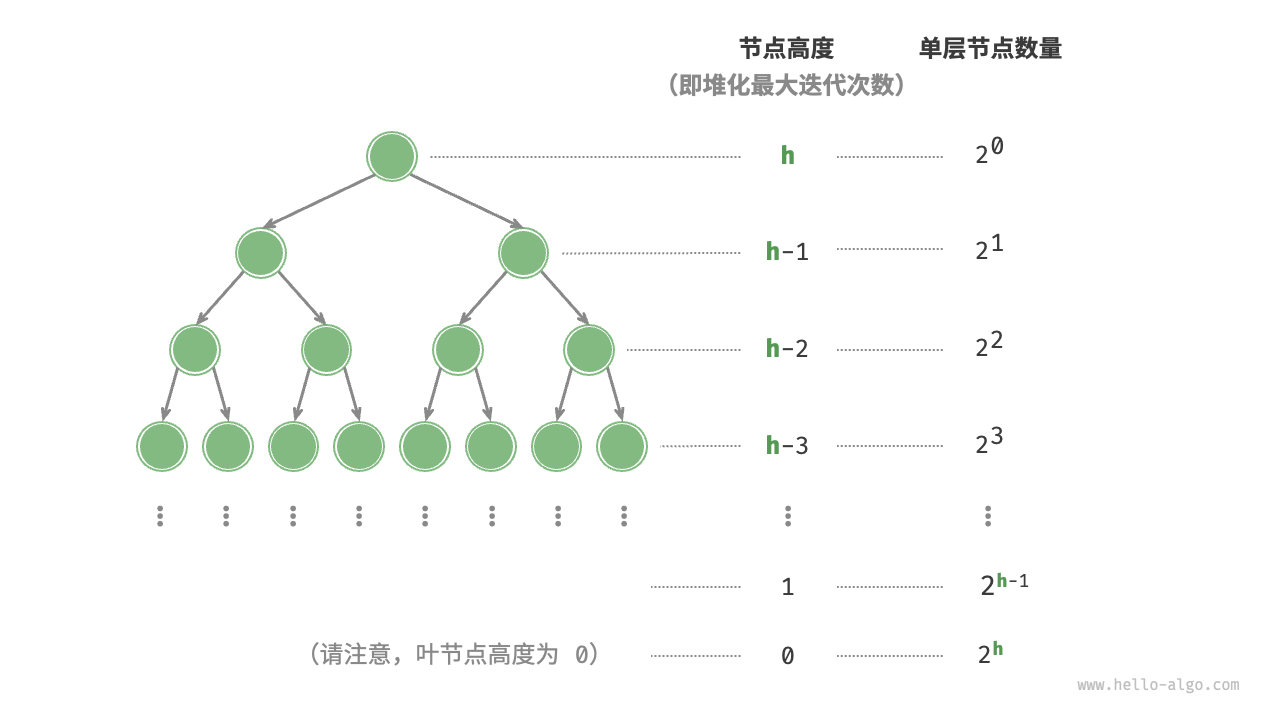
图 8-5 完美二叉树的各层节点数量

如图 8-5 所示，节点“从顶至底堆化”的最大迭代次数等于该节点到叶节点的距离，而该距离正是“节点高度”。因此，我们可以对各层的“节点数量 × 节点高度”求和，得到所有节点的堆化迭代次数的总和。

T(h)=20h+21(h−1)+22(h−2)+⋯+2(h−1)×1

化简上式需要借助中学的数列知识，先将 T(h) 乘以 2 ，得到：

T(h)=20h+21(h−1)+22(h−2)+⋯+2h−1×12T(h)=21h+22(h−1)+23(h−2)+⋯+2h×1

使用错位相减法，用下式 2T(h) 减去上式 T(h) ，可得：

2T(h)−T(h)=T(h)=−20h+21+22+⋯+2h−1+2h

观察上式，发现 T(h) 是一个等比数列，可直接使用求和公式，得到时间复杂度为：

T(h)=21−2h1−2−h=2h+1−h−2=O(2h)

进一步，高度为 h 的完美二叉树的节点数量为 n=2h+1−1 ，易得复杂度为 O(2h)=O(n) 。以上推算表明，输入列表并建堆的时间复杂度为 O(n) ，非常高效。

8.3 Top-k 问题

Question

给定一个长度为 n 的无序数组 nums ，请返回数组中最大的 k 个元素。

对于该问题，我们先介绍两种思路比较直接的解法，再介绍效率更高的堆解法。

8.3.1 方法一：遍历选择

我们可以进行图 8-6 所示的 k 轮遍历，分别在每轮中提取第 1、2、…、k 大的元素，时间复杂度为 O(nk) 。

此方法只适用于 k≪n 的情况，因为当 k 与 n 比较接近时，其时间复杂度趋向于 O(n2) ，非常耗时。

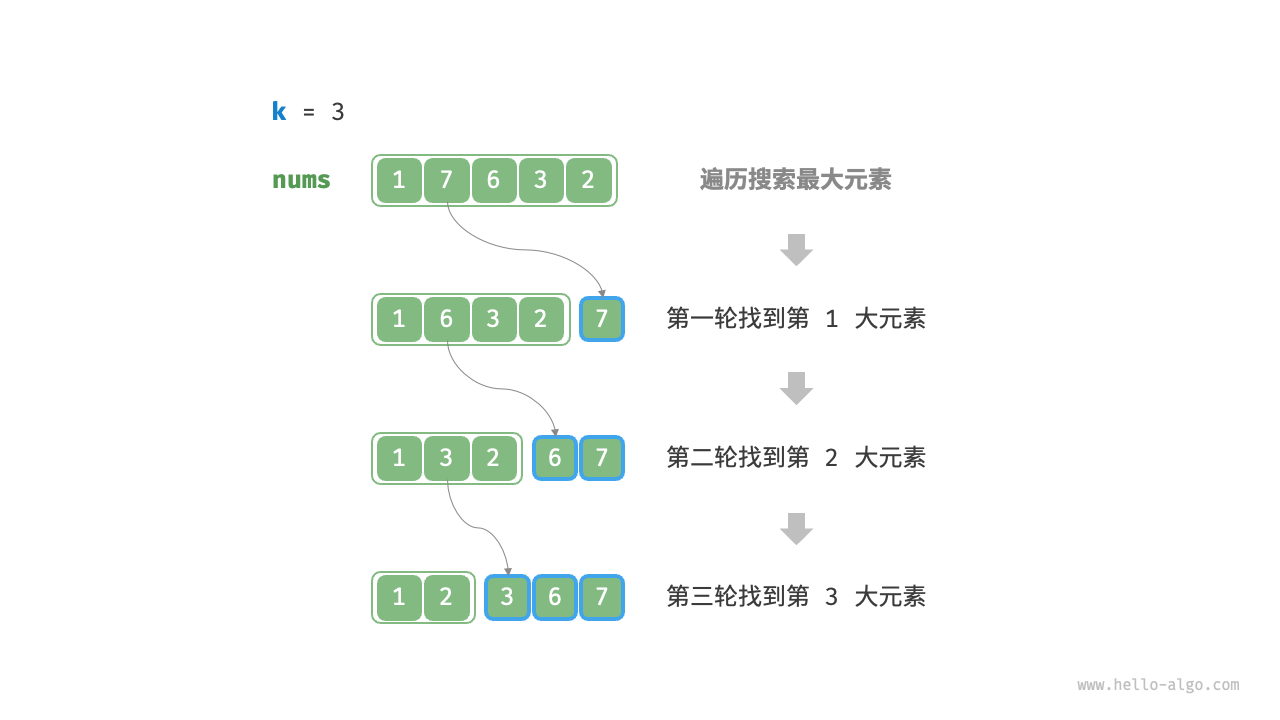
图 8-6 遍历寻找最大的 k 个元素

Tip

当 k=n 时，我们可以得到完整的有序序列，此时等价于“选择排序”算法。

8.3.2 方法二：排序

如图 8-7 所示，我们可以先对数组 nums 进行排序，再返回最右边的 k 个元素，时间复杂度为 O(nlog⁡n) 。

显然，该方法“超额”完成任务了，因为我们只需找出最大的 k 个元素即可，而不需要排序其他元素。

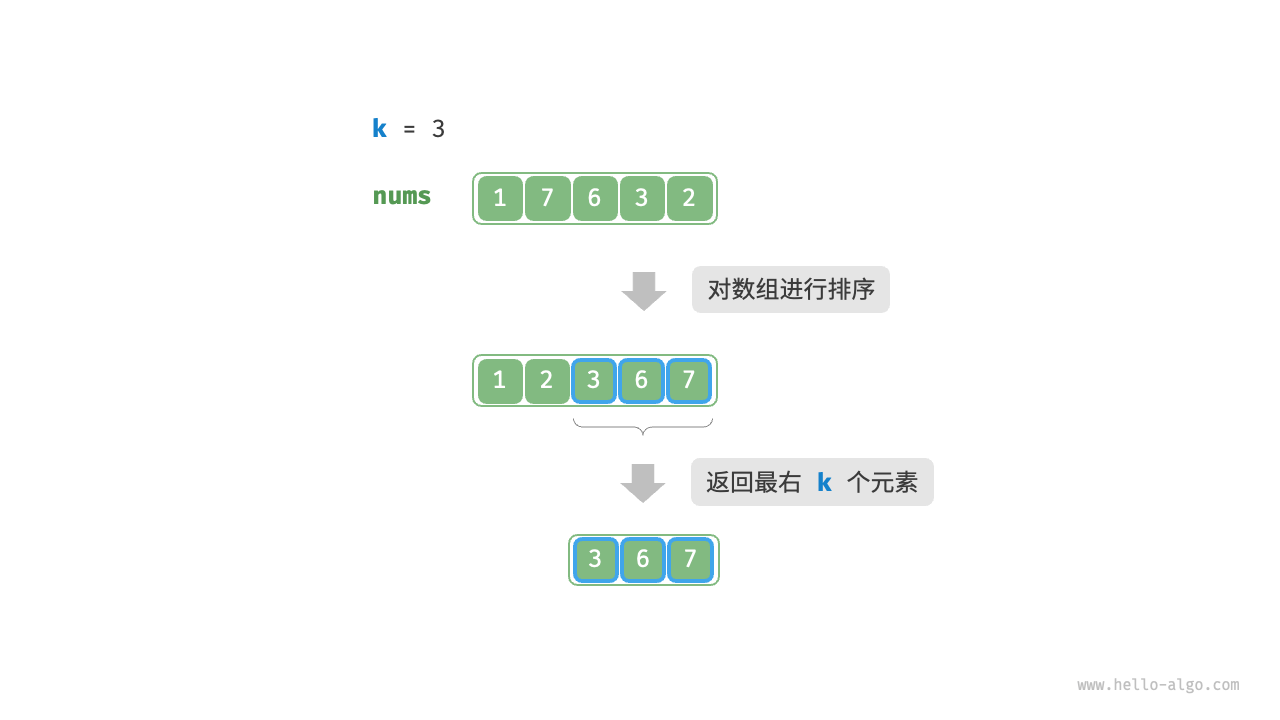
图 8-7 排序寻找最大的 k 个元素

8.3.3 方法三：堆

我们可以基于堆更加高效地解决 Top-k 问题，流程如图 8-8 所示。

  1. 初始化一个小顶堆，其堆顶元素最小。
  2. 先将数组的前 k 个元素依次入堆。
  3. 从第 k+1 个元素开始，若当前元素大于堆顶元素，则将堆顶元素出堆，并将当前元素入堆。
  4. 遍历完成后，堆中保存的就是最大的 k 个元素。

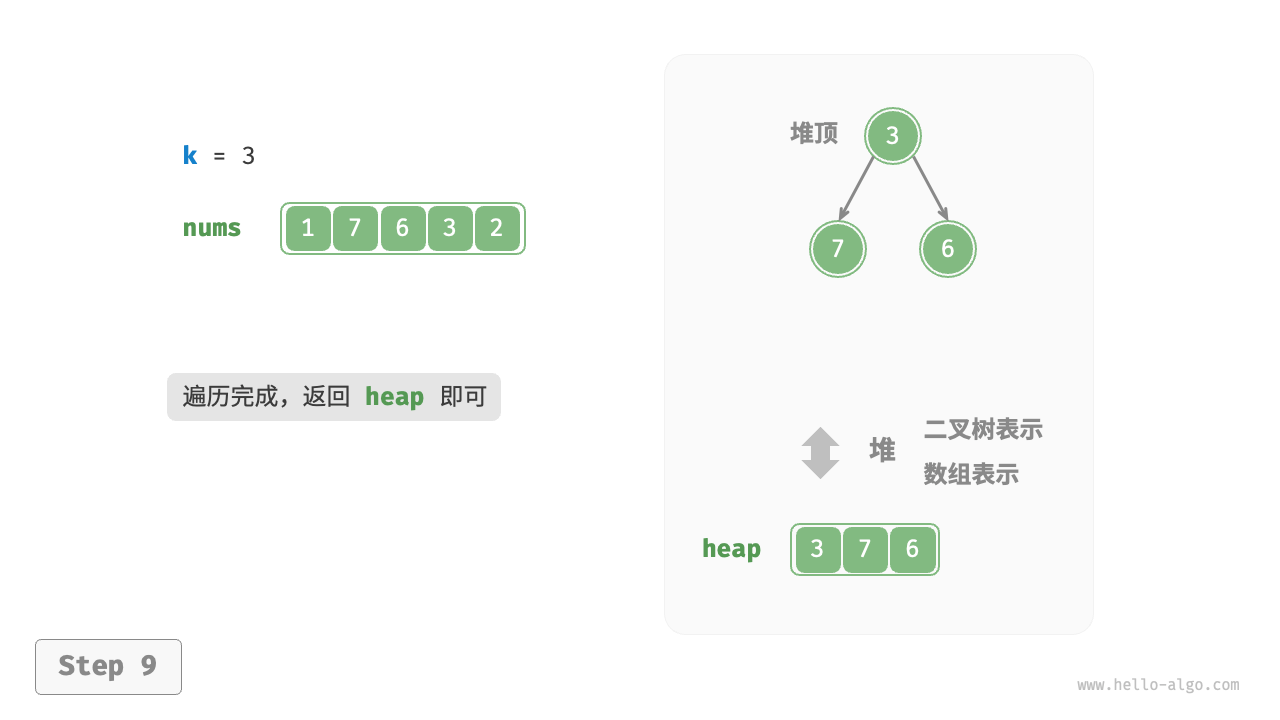
图 8-8 基于堆寻找最大的 k 个元素

示例代码如下：

/* 基于堆查找数组中最大的 k 个元素 */
priority_queue<int, vector<int>, greater<int>> topKHeap(vector<int> &nums, int k) {
    // 初始化小顶堆
    priority_queue<int, vector<int>, greater<int>> heap;
    // 将数组的前 k 个元素入堆
    for (int i = 0; i < k; i++) {
        heap.push(nums[i]);
    }
    // 从第 k+1 个元素开始，保持堆的长度为 k
    for (int i = k; i < nums.size(); i++) {
        // 若当前元素大于堆顶元素，则将堆顶元素出堆、当前元素入堆
        if (nums[i] > heap.top()) {
            heap.pop();
            heap.push(nums[i]);
        }
    }
    return heap;
}

可视化运行

总共执行了 n 轮入堆和出堆，堆的最大长度为 k ，因此时间复杂度为 O(nlog⁡k) 。该方法的效率很高，当 k 较小时，时间复杂度趋向 O(n) ；当 k 较大时，时间复杂度不会超过 O(nlog⁡n) 。

另外，该方法适用于动态数据流的使用场景。在不断加入数据时，我们可以持续维护堆内的元素，从而实现最大的 k 个元素的动态更新。

8.4 小结

1. 重点回顾

  • 堆是一棵完全二叉树，根据成立条件可分为大顶堆和小顶堆。大（小）顶堆的堆顶元素是最大（小）的。
  • 优先队列的定义是具有出队优先级的队列，通常使用堆来实现。
  • 堆的常用操作及其对应的时间复杂度包括：元素入堆 O(log⁡n)、堆顶元素出堆 O(log⁡n) 和访问堆顶元素 O(1) 等。
  • 完全二叉树非常适合用数组表示，因此我们通常使用数组来存储堆。
  • 堆化操作用于维护堆的性质，在入堆和出堆操作中都会用到。
  • 输入 n 个元素并建堆的时间复杂度可以优化至 O(n) ，非常高效。
  • Top-k 是一个经典算法问题，可以使用堆数据结构高效解决，时间复杂度为 O(nlog⁡k) 。

2. Q & A

Q：数据结构的“堆”与内存管理的“堆”是同一个概念吗？

两者不是同一个概念，只是碰巧都叫“堆”。计算机系统内存中的堆是动态内存分配的一部分，程序在运行时可以使用它来存储数据。程序可以请求一定量的堆内存，用于存储如对象和数组等复杂结构。当这些数据不再需要时，程序需要释放这些内存，以防止内存泄漏。相较于栈内存，堆内存的管理和使用需要更谨慎，使用不当可能会导致内存泄漏和野指针等问题。

我要求数组中的第K个最大元素，应该用大顶堆还是小顶堆？

要求数组中的第k个最大元素，使用小顶堆更为合适，以下是详细原因：

小顶堆的优势

  1. 整体思路
    • 首先构建一个包含数组所有元素的小顶堆，此时堆顶元素是整个数组中的最小值。
    • 然后进行k - 1次删除堆顶元素的操作，并在每次删除后调整堆，使堆保持小顶堆的性质。
    • 经过k - 1次操作后，堆顶元素就是第k个最大的元素。
  1. 时间复杂度分析
    • 构建小顶堆的时间复杂度为

      （使用标准的自下而上的建堆算法）。
    • 每次删除堆顶元素并调整堆的时间复杂度为

      ，总共需要进行k - 1次删除操作，所以这部分的时间复杂度为

      。
    • 因此，总的时间复杂度为

      。当k相对较小时（例如，

      ），时间复杂度近似为

      ，这在处理大规模数据时效率较高。
  1. 空间复杂度分析
    • 构建小顶堆需要额外的空间来存储堆结构，但在实际实现中，可以通过原地建堆的方式将空间复杂度优化到

      （不考虑递归调用栈等少量额外空间）。即直接在原数组上进行堆操作，不需要额外开辟大量的存储空间来存储堆元素，只需要几个指针变量来辅助操作。

大顶堆的不足

  1. 整体思路及问题
    • 如果使用大顶堆来解决此问题，通常的做法是先构建一个包含数组前k个元素的大顶堆，然后遍历数组中剩余的n - k个元素，若当前元素大于堆顶元素，则替换堆顶元素并调整堆。
    • 虽然在某些情况下这种方法也能得到正确结果，但它存在一些问题。
  1. 时间复杂度分析
    • 构建大小为k的大顶堆的时间复杂度为

      （使用优化的Floyd建堆算法）。
    • 遍历剩余n - k个元素并调整堆的时间复杂度为

      。
    • 总的时间复杂度为

      。当k较大时（接近n），时间复杂度会接近

      ，不如小顶堆在k较小时的时间复杂度性能好。
  1. 空间复杂度分析
    • 构建大顶堆需要额外的空间来存储k个元素，空间复杂度为

      。相比小顶堆在优化后的空间复杂度

      ，大顶堆在空间利用上可能不够高效，尤其是在处理大规模数据且k较大时，可能会占用较多的内存空间。

综上所述，在求数组中的第k个最大元素时，使用小顶堆在时间和空间复杂度方面通常具有更好的性能表现，尤其是当k相对较小时优势更为明显。当然，在实际应用中，还需要根据具体的数据特点、内存限制等因素综合考虑选择合适的方法。

优先队列：

大根堆

//
// Created by 25678 on 2024/10/30.
//

#ifndef GUC_MYMAXHEAP_H
#define GUC_MYMAXHEAP_H
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;

class myMaxHeap {
private:    // 私有的，就让他自己私下进行操作，公开的即是暴露出去的接口
    vector<int> heap;

    // 底层交换操作
    void mySwap(int a, int b) {
        int temp = heap[a];
        heap[a] = heap[b];
        heap[b] = temp;
    }

    // 上移操作,调整堆，使以i为根节点的子树满足小顶堆性质
    void heapifyUp(int index){  // 堆尾往上移动，直到他的父亲都比他小
        // 根要去和他的父亲比较，谁大谁就去当根，直到他的父亲都比他大
        while (index > 0 && heap[(index - 1) / 2] < heap[index]) {
            mySwap((index - 1) / 2, index);
            index = (index - 1) / 2;
        }
    }

    // 下滑操作,调整堆，使以i为根节点的子树满足大顶堆性质
    void heapifyDown(int index){
        // 根要去和他的左右孩子比较，谁大谁就去当根，直到他的左右孩子都比他小
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        int largest = index;

        if (left < heap.size() && heap[left] > heap[largest]) {
            largest = left;
        }

        if (right < heap.size() && heap[right] > heap[largest]) {
            largest = right;
        }

        if (largest!= index) {
            mySwap(index, largest);
            heapifyDown(largest);
        }
    }

public:
    // 构造函数
    myMaxHeap() {}

    // 插入元素
    void push(int value) {
        heap.push_back(value);
        heapifyUp(heap.size() - 1);
    }

    // 删除堆顶元素
    void extractTop() {
        if (heap.empty()) {
            cerr << "Heap is empty." << endl;
            return;
        }
        int maxValue = heap[0];
        heap[0] = heap.back();
        heap.pop_back();
        heapifyDown(0);
    }

    // 获取堆顶元素
    int pop(){
        if (heap.empty()) {
            cerr << "Heap is empty." << endl;
            return -1;
        }
        cout << heap[0] << endl;
        return heap[0];
    }

    // 获取堆中元素的数量
    int size() {
        return heap.size();
    }

    // 堆是否为空
    bool isEmpty() {
        if (heap.size() == 0){
            cout << "Heap is empty." << endl;
            return true;
        }else{
            return false;
        }
    }
};


#endif //GUC_MYMAXHEAP_H

小根堆

//
// Created by 25678 on 2024/10/30.
//

#ifndef GUC_MYMAXHEAP_H
#define GUC_MYMAXHEAP_H
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;

class myMinHeap {
private:    // 私有的，就让他自己私下进行操作，公开的即是暴露出去的接口
    vector<int> heap;

    // 底层交换操作
    void mySwap(int a, int b) {
        int temp = heap[a];
        heap[a] = heap[b];
        heap[b] = temp;
    }

    // 上移操作,调整堆，使以i为根节点的子树满足小顶堆性质
    void heapifyUp(int index){  // 堆尾往上移动，直到他的父亲都比他小
        // 根要去和他的父亲比较，谁大谁就去当根，直到他的父亲都比他大
//        while (index > 0 && heap[(index - 1) / 2] < heap[index]) {
//            mySwap((index - 1) / 2, index);
//            index = (index - 1) / 2;
//        }
        while (index > 0 && heap[index] > heap[(index - 1) / 2]) {
            mySwap(index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    // 下滑操作,调整堆，使以i为根节点的子树满足大顶堆性质
    void heapifyDown(int index){
        // 根要去和他的左右孩子比较，谁大谁就去当根，直到他的左右孩子都比他小
        int left = 2 * index + 1;
        int right = 2 * index + 2;
//        int largest = index;
//
//        if (left < heap.size() && heap[left] > heap[largest]) {
//            largest = left;
//        }
//
//        if (right < heap.size() && heap[right] > heap[largest]) {
//            largest = right;
//        }
//
//        if (largest!= index) {
//            mySwap(index, largest);
//            heapifyDown(largest);
//        }
        int smallest = index;

        if (left < heap.size() && heap[left] < heap[smallest]) {
            smallest = left;
        }

        if (right < heap.size() && heap[right] < heap[smallest]) {
            smallest = right;
        }

        if (smallest!= index) {
            mySwap(index, smallest);
            heapifyDown(smallest);
        }
    }


};


#endif //GUC_MYMAXHEAP_H

main函数

/*
    Name:
    Copyright:
    Author: 
    Date: <DATETIME>
    Description:
*/
#include <bits/stdc++.h>
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include "myMaxHeap.h"

using namespace std;

int main() {
    // 创建一个最小堆优先队列，需要传入比较函数
    priority_queue<int, vector<int>, greater<int>> minHeap;

    // 向优先队列中插入元素
    minHeap.push(5);
    minHeap.push(10);
    minHeap.push(3);
    minHeap.push(8);

    // 输出优先队列的大小
    cout << "优先队列大小: " << minHeap.size() << std::endl;

    // 访问堆顶元素（最小值）
    cout << "堆顶元素（最小值）: " << minHeap.top() << std::endl;

    // 弹出堆顶元素
    minHeap.pop();

    // 再次输出堆顶元素
    cout << "弹出一个元素后，堆顶元素: " << minHeap.top() << endl;
    //------------------------------------上述为函数调用，下面为自定义类的优先队列-------------
    myMaxHeap maxHeap;
    // 向优先队列中插入元素
    maxHeap.push(5);
    maxHeap.push(10);
    maxHeap.push(3);
    maxHeap.push(8);

    // 输出优先队列的大小
    cout << "优先队列大小: " << maxHeap.size() << endl;

    // 访问堆顶元素（最大值）
    cout << "堆顶元素（最大值）为： " << maxHeap.pop() << endl;

    // 弹出堆顶元素
    maxHeap.extractTop();

    // 访问堆顶元素（最大值）
    cout << "堆顶元素（最大值）为： " << maxHeap.pop() << endl;

    return 0;
}

堆排序：

main函数

/*
    Name:
    Copyright:
    Author: 
    Date: <DATETIME>
    Description:
*/
#include <bits/stdc++.h>
#include <iostream>
#include <vector>
#include <string>
#include "myHeapSort.h"

using namespace std;

int main() {
    vector<int> nums = {1, 12, 11, 13, 5, 6, 73, 14, 5, 36, 77, 28, 39};
    cout << "排序前的数组: ";
    for (int i = 0; i < nums.size(); i++) {
        cout << nums[i] << " ";
    }
    cout << endl;
    myHeapSort(nums);
    cout << "排序后的数组: ";
    for (int i = 0; i < nums.size(); i++) {
        cout << nums[i] << " ";
    }
    cout << endl;

    //--------------------------下面是函数调用----------------------------------------------------
    // 构建最大堆
    make_heap(nums.begin(), nums.end(), greater<int>());
    // 排序
    sort_heap(nums.begin(), nums.end(), greater<int>());
    cout << "排序后的数组: ";
    for (int i = 0; i < nums.size(); i++) {
        cout << nums[i] << " ";
    }
    cout << endl;
    // Your code here
    return 0;
}

myHeapSort：

//
// Created by 25678 on 2024/10/30.
//

#ifndef GUC_MYHEAPSORT_H
#define GUC_MYHEAPSORT_H

#include <vector>
using namespace std;

// 堆排序
void myHeapSort(vector<int>& nums);

void heapify(vector<int> &vector, int i, int i1);

void heapSort(vector<int>& nums){
    int n = nums.size();
    // 建堆
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(nums, n, i);
    }
    // 排序
    for (int i = n - 1; i > 0; i--) {
        // 交换根元素和最后一个元素
        swap(nums[0], nums[i]);
        // 重新调整根元素为最大堆
        heapify(nums, i, 0);
    }
}

void heapify(vector<int> &nums, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if (left < n && nums[left] > nums[largest]) {
        largest = left;
    }
    if (right < n && nums[right] > nums[largest]) {
        largest = right;
    }

    if (largest!= i) {
        swap(nums[i], nums[largest]);
        // 交换后，largest 可能不再是大根堆，需要自下而上，构建大根堆
        heapify(nums, n, largest);
    }

}

 自上而下，构建大根堆
//void heapify(vector<int>& nums, int n, int i){
//    int largest = i;
//    int left = 2 * i + 1;
//    int right = 2 * i + 2;
//
//    if (left < n && nums[left] > nums[largest]) {
//        largest = left;
//    }
//    if (right < n && nums[right] > nums[largest]) {
//        largest = right;
//    }
//
//    if (largest!= i) {
//        swap(nums[i], nums[largest]);
//        // 交换后，largest 可能不再是大根堆，需要自下而上，构建大根堆
//        heapify(nums, n, largest);
//    }
//}


class myHeapSort{
    // 私有的，就让他自己私下进行操作，公开的即是暴��出去的接口
public:
    void heapSort(vector<int>& nums){
        int n = nums.size();
        // 建堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(nums, n, i);
        }
        // 排序
        for (int i = n - 1; i > 0; i--) {
            // 交换根元素和最后一个元素
            swap(nums[0], nums[i]);
            // 重新调整根元素为最大堆
            heapify(nums, i, 0);
        }
    }

    // 自上而下，构建大根堆
    void heapify(vector<int>& nums, int n, int i){
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;

        if (left < n && nums[left] > nums[largest]) {
            largest = left;
        }
        if (right < n && nums[right] > nums[largest]) {
            largest = right;
        }

        if (largest!= i) {
            swap(nums[i], nums[largest]);
            // 交换后，largest 可能不再是大根堆，需要自下而上，构建大根堆
            heapify(nums, n, largest);
        }
    }

};


#endif //GUC_MYHEAPSORT_H

获取最大的K个元素：

/*
    Name:
    Copyright:
    Author: 
    Date: <DATETIME>
    Description:
*/
#include <bits/stdc++.h>
#include <iostream>
#include <vector>
#include <string>

using namespace std;
getLargestK(vector<int> arrays, int k);

int main() {
    vector<int> arrays = {5, 3, 8, 10, 2, 7, 6, 4};
    int k;
    cin >> k;
    vector<int> resultOfLagestK = getLargestK(arrays, k);
    cout << "最大的 " << k << " 个元素为: ";
    for (int i = 0; i < resultOfLagestK.size(); i++) {
        cout << resultOfLagestK[i] << " ";
    }
    cout << endl;
    // Your code here
    return 0;
}

vector<int> getLargestK(vector<int> arrays, int k) {
    // 构建最小堆
    make_heap(arrays.begin(), arrays.end(), greater<int>());
    // 排序
    sort_heap(arrays.begin(), arrays.end(), greater<int>());
    // 取出前k个元素
    vector<int> resultOfLagestK;
    for (int i = 0; i < k; i++) {
        if(minHeap.size() < k){
            minHeap.push_back(arrays[i]);
        }else if(minHeap.top() < arrays[i]){
            minHeap.pop();
            minHeap.push(arrays[i]);
        }
    }
    vector<int> resultOfLagestK;
    while(!minHeap.empty()){
        resultOfLagestK.push_back(minHeap.top());
        minHeap.pop();
    }
    return resultOfLagestK;
}


http://www.kler.cn/a/372282.html

相关文章：

  • Linux：操作系统不朽的传说
  • OpenGL材质系统和贴图纹理
  • CSS3——3. 书写格式二
  • 后端开发-Maven
  • Python 数据结构揭秘：栈与队列
  • CSS——1.优缺点
  • 医院信息化与智能化系统(13)
  • React Query已过时？新一代请求工具横空出世
  • 日本也有九九乘法表？你会读吗？柯桥零基础学日语到蓝天广场
  • openharmony北向开发入门教程汇总
  • 【非关系型分布式数据库】HBase从入门到面试学习总结
  • Python实现随机分布式延迟PSO优化算法(RODDPSO)优化DBSCAN膨胀聚类模型项目实战
  • IDEA 安装热部署 JRebel -新版-亲测有效
  • Android13预置应用及授权开发
  • Thread类及线程的核心操作
  • Java集合常见面试题总结(5)
  • 常见的开发工具及其作用
  • [论文阅读] GPT-4 Technical Report
  • Kotlin-协程基础
  • 【面试经典150】day 9
  • PostgreSQL 清理 WAL 文件
  • 2024“源鲁杯“高校网络安全技能大赛-Misc-WP
  • 逆变器竞品分析--绿联150W方案【2024/10/30】
  • Docker搭建官方私有仓库registry及相关配置
  • 基于树莓派的安保巡逻机器人--（一、快速人脸录入与精准人脸识别）
  • DGUS屏使用方法