当前位置：首页 > article >正文

数据结构和算法-动态规划(1)-认识动态规划

article 2024/10/31 18:45:40

认识动态规划

什么是动态规划

Dynamic Programming is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems.

动态规划(Dynamic Programming): 计算并存储小问题的解，并将这些解组合成大问题的解。

动态规划如何工作

用一句名言开启

Those Who Cannot Remember the Past Are Condemned(危险的) To Repeat It。

- 不记得过去的人注定要重蹈覆辙。

看一个例子

计算: 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1 = ？

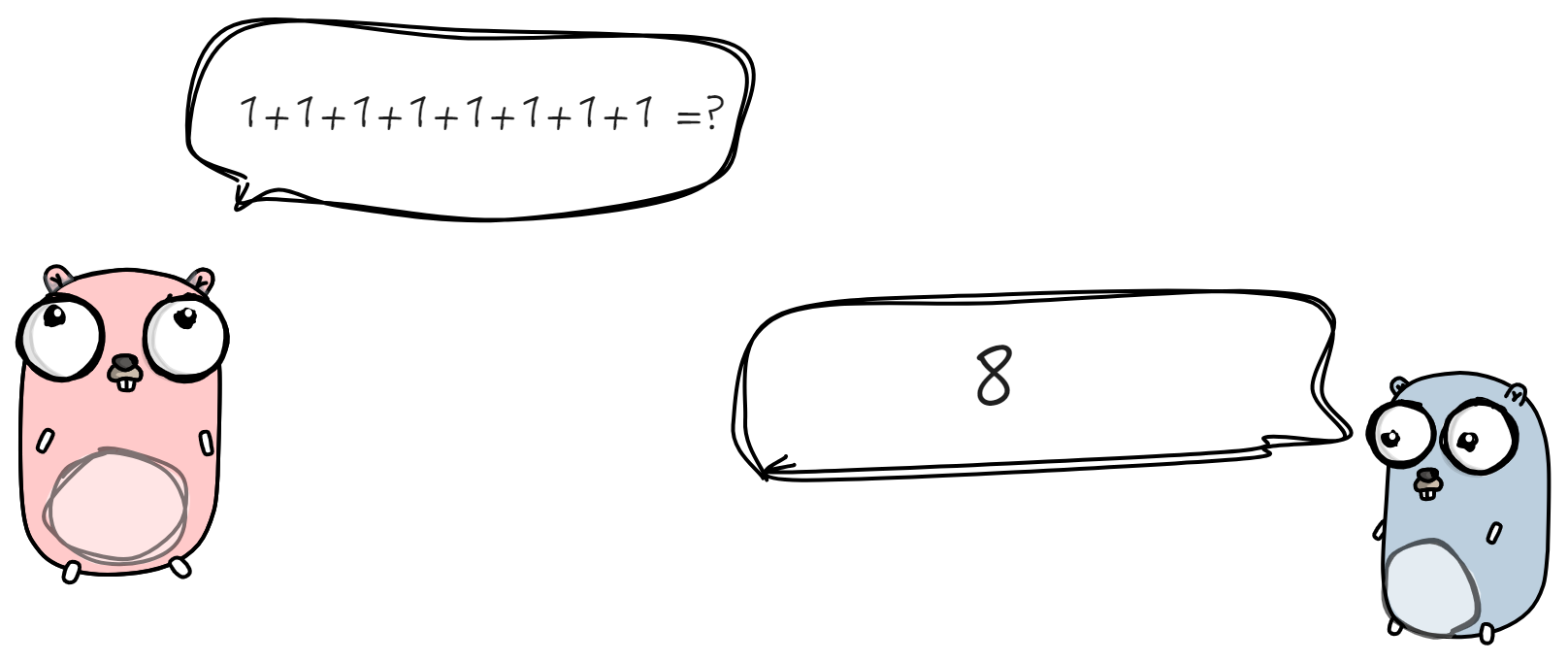
如果在等式左边添加1+，即 **1 + **1 + 1 + 1 + 1 + 1+ 1 + 1 + 1=？

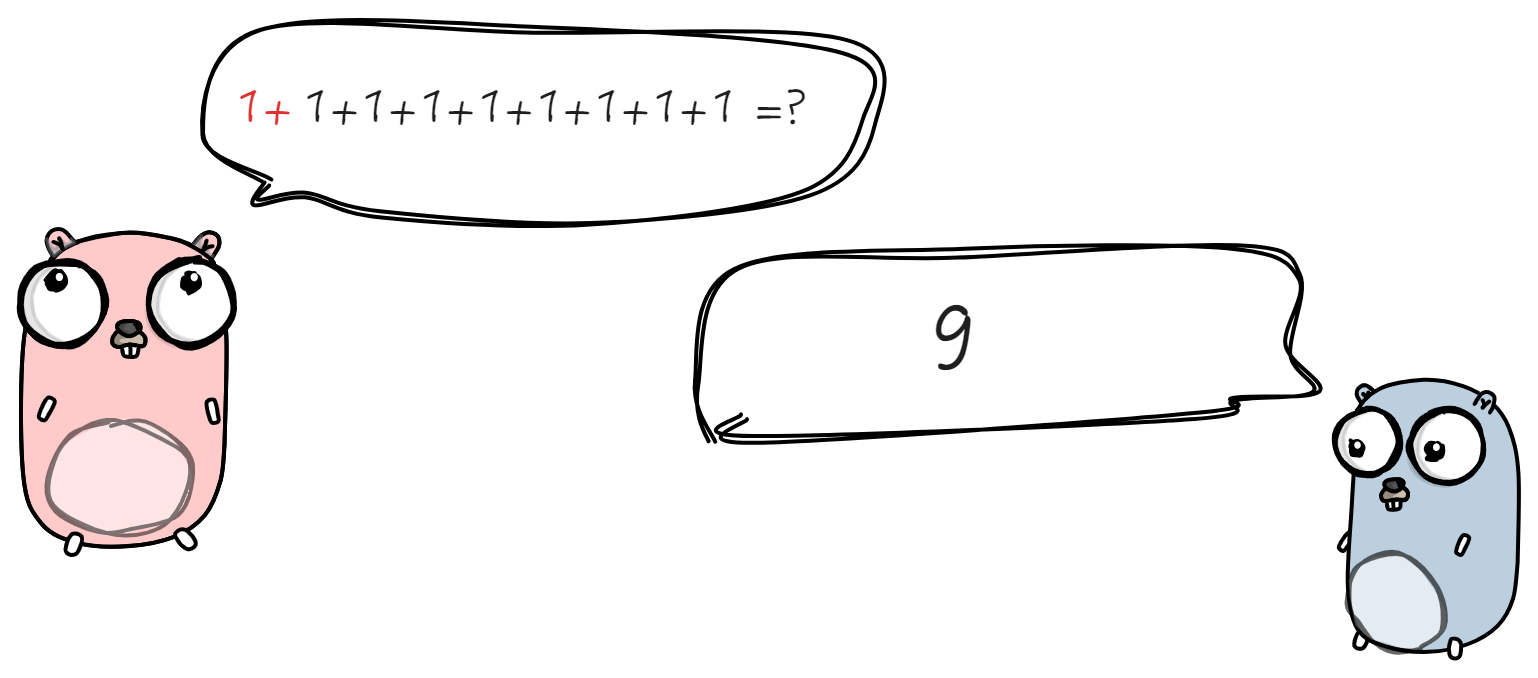
如何快速的计算出答案？

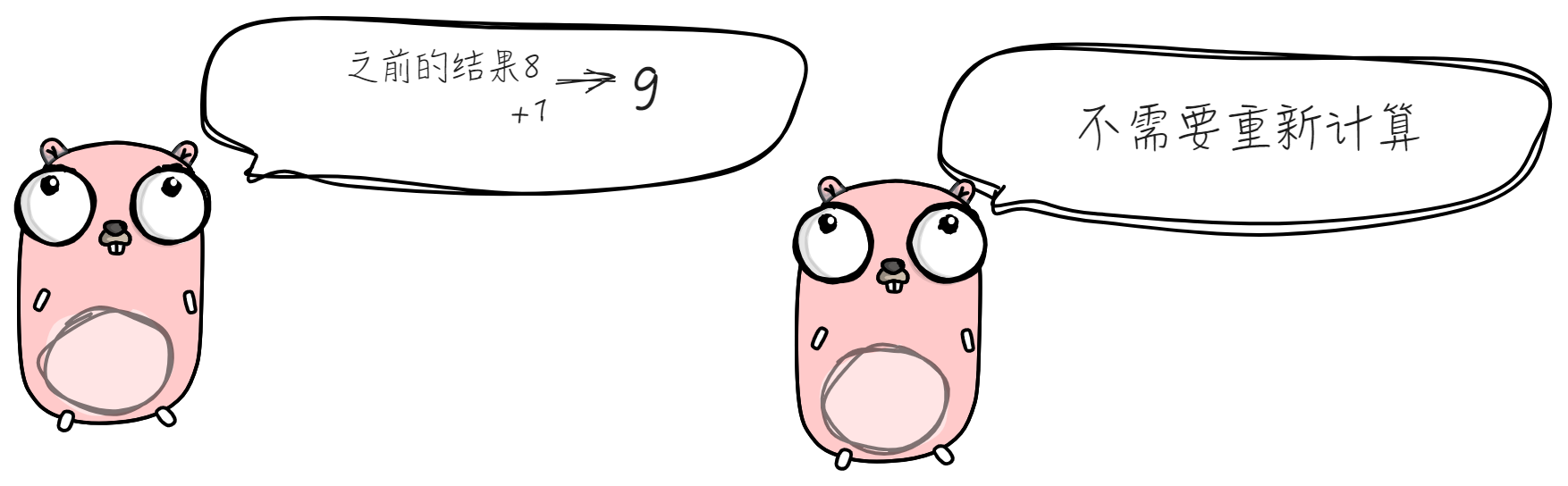
动态规划思路: 记住之前的求解，节省时间。

再谈斐波拉切数列(Fibonacci )

兔子问题

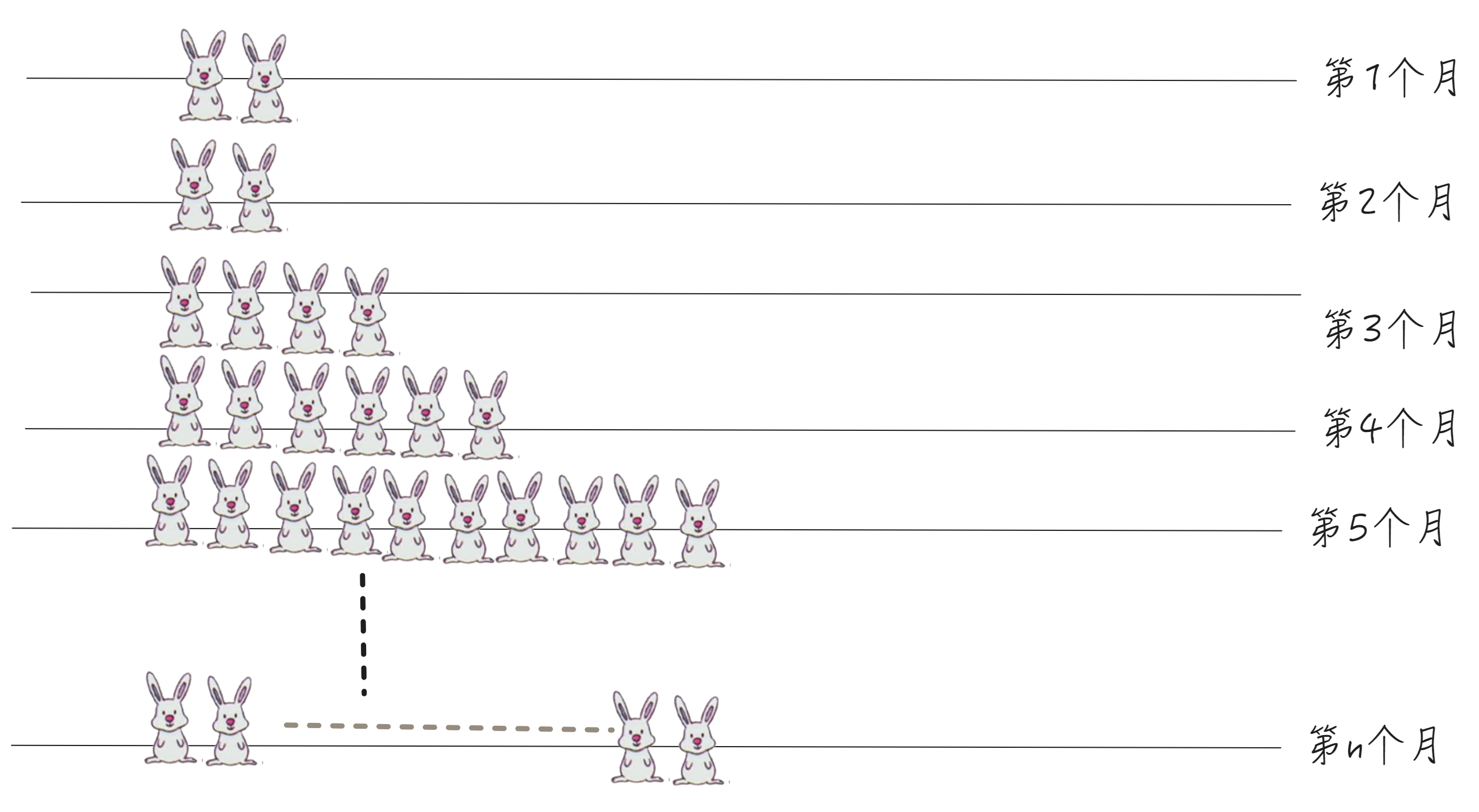
找出斐波拉切数列的数学归纳

分两种情况分析：

n=1,n=2 , 结果为 1
n>2, 结果为 n* (n-1) , n表示当前月

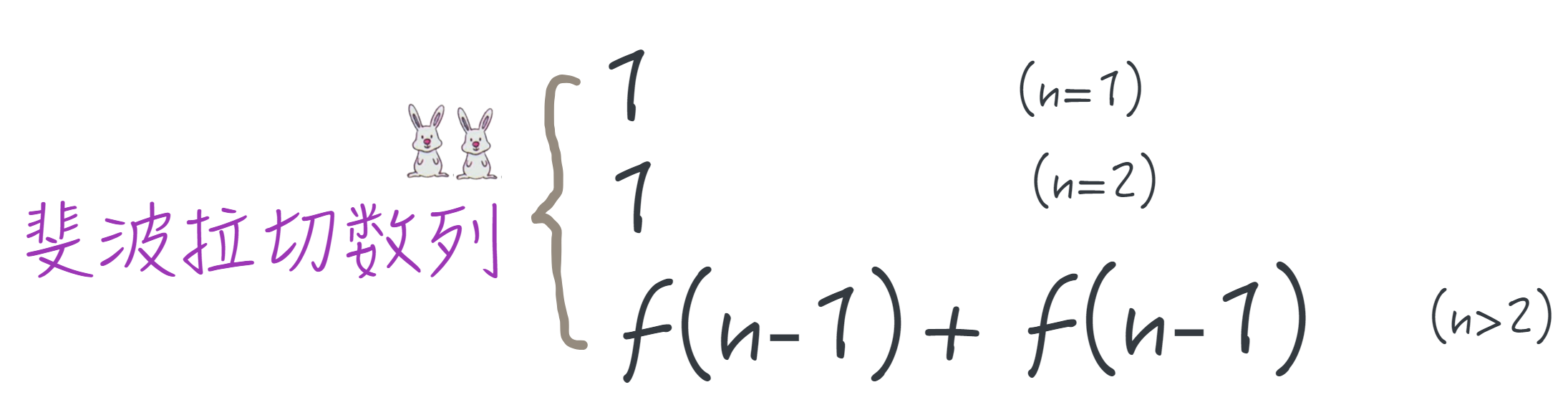
构建代码(递归实现)

public int fib(int n) {
    if (n == 1 || n == 2) return 1;
    int res = fib(n - 1) + fib(n-2);
    return res;
}

分析递归实现

我们按照递归树进行分析，构建递归树模型。

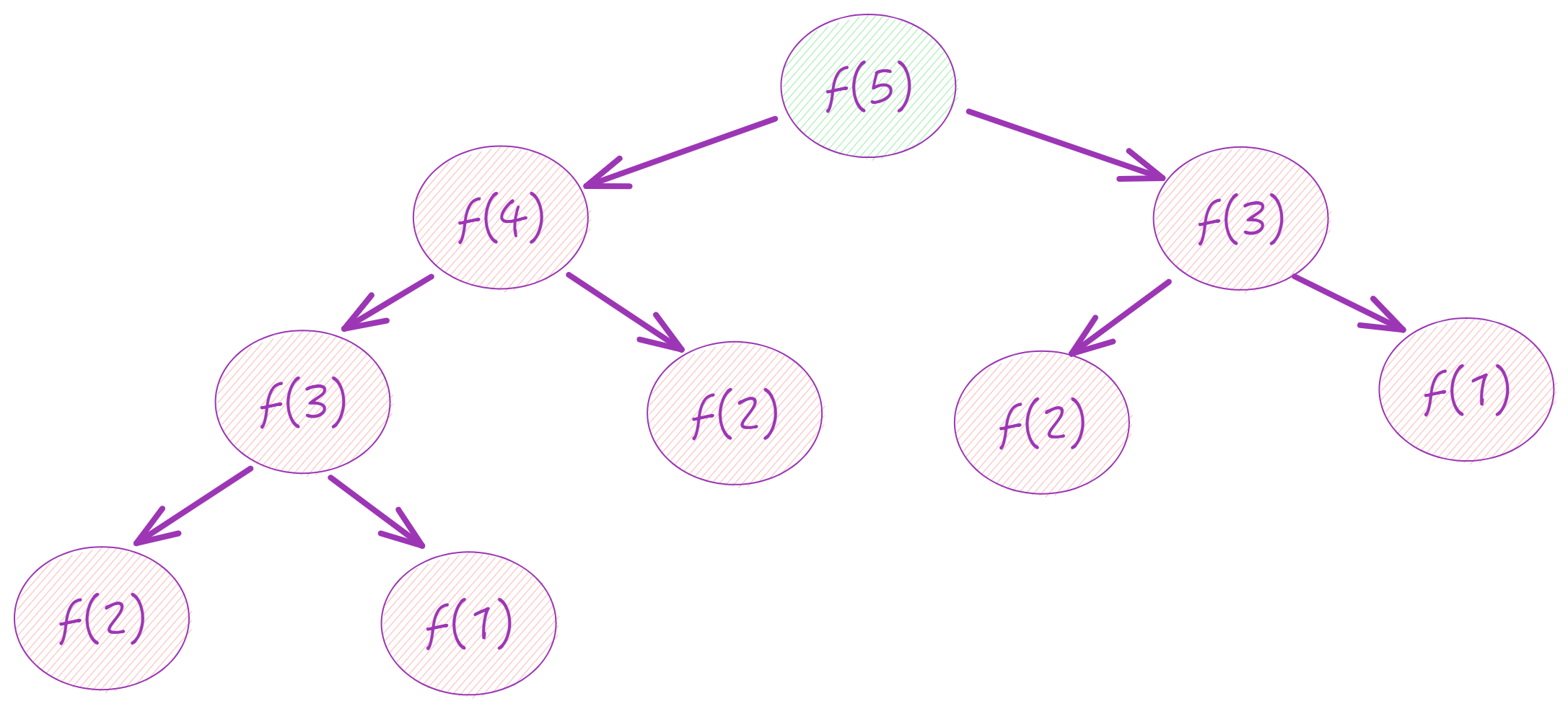
递归模型树的问题

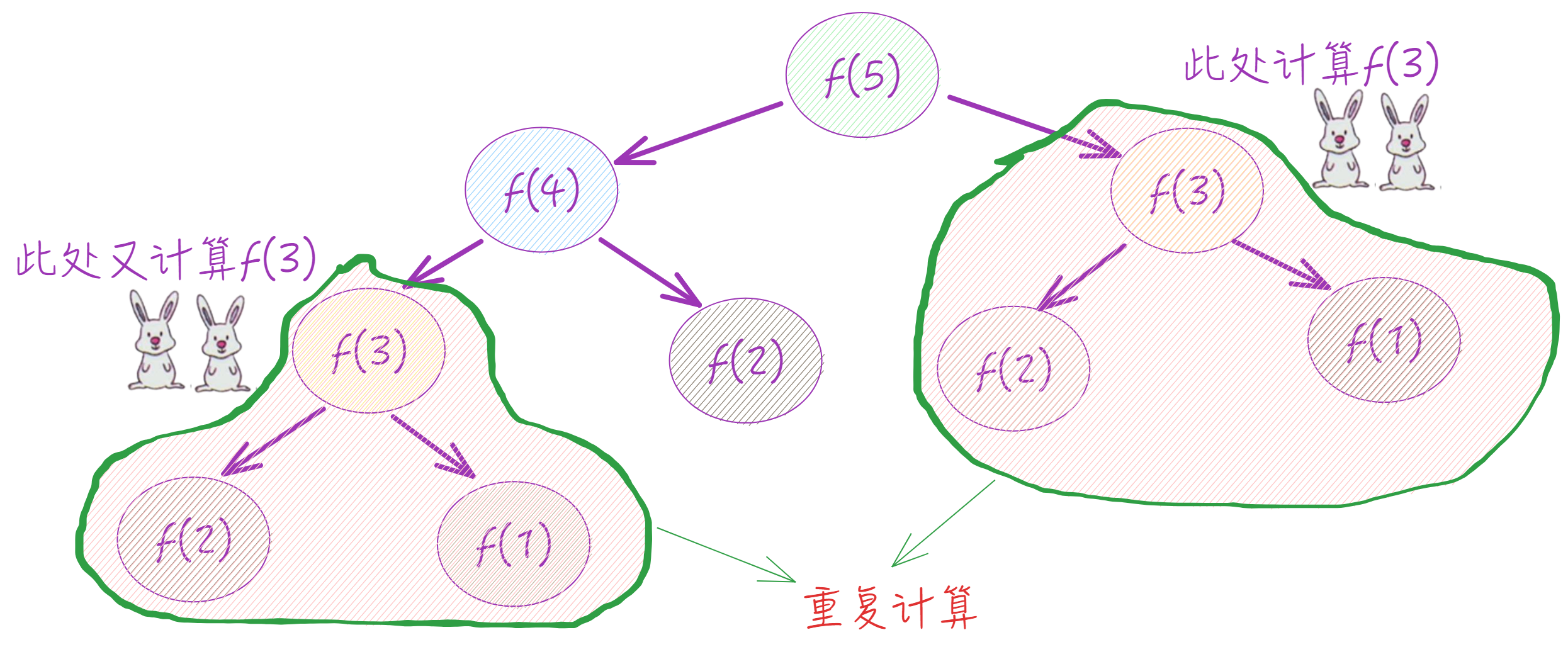优化方案

备忘录

自定向下的备忘录记忆,使用一个集合(数组)记录计算的结果防止重复计算。

package com.ffyc.dp;

public class Fib02 {

    public void fib(int n) {
        int[] remember = new int[n + 1]; //不使用n=0
        System.out.println(f(n, remember));
    }

    private int f(int n, int[] remember) {
        //如果remember中指定位置已经记录则直接返回,防止重复计算
        if (remember[n] != 0) {
            return remember[n];
        }
        //如果n==1,n==2则remember[1]=1, remember[2]=1
        if (n == 1 || n == 2) {
            remember[n] = 1;
        } else {
            remember[n] = f(n - 1, remember) + f(n - 2, remember);
        }
        return remember[n];
    }

    public static void main(String[] args) {
        new Fib02().fib(5);
    }
}

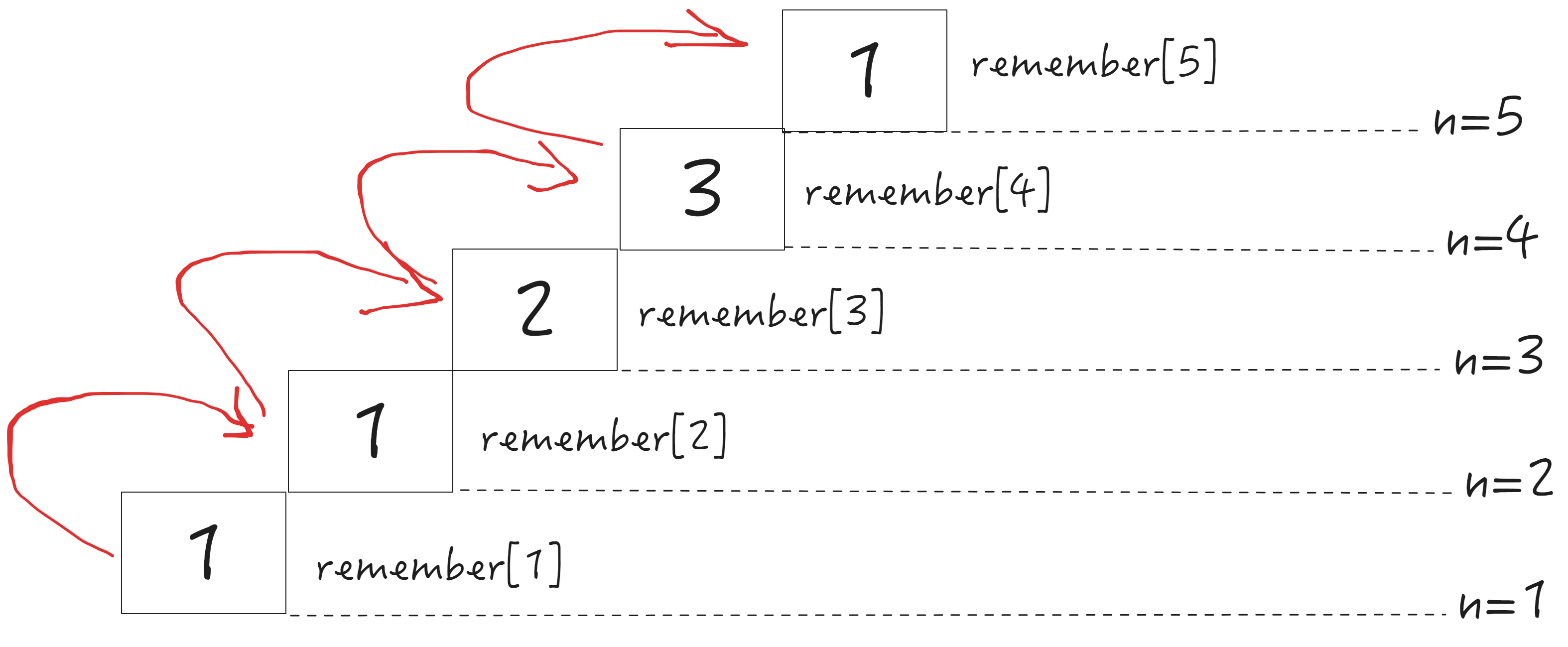
自低向上的动态规划

public class Fib003 {
    public  int fib(int n){
        int[] remember = new int[n+1];

        remember[1] =1;
        remember[2] =1;

        for(int i = 3;i<=n;i++){
            remember[i] = remember[i-1]+ remember[i-2];
        }
        return remember[n];
    }

    public static void main(String[] args) {
        System.out.println(new Fib003().fib(5));
    }
}

实际上当前这个数组可以压缩为两个变量(a,b),当前的数由a，b迭代完成。–状态压缩

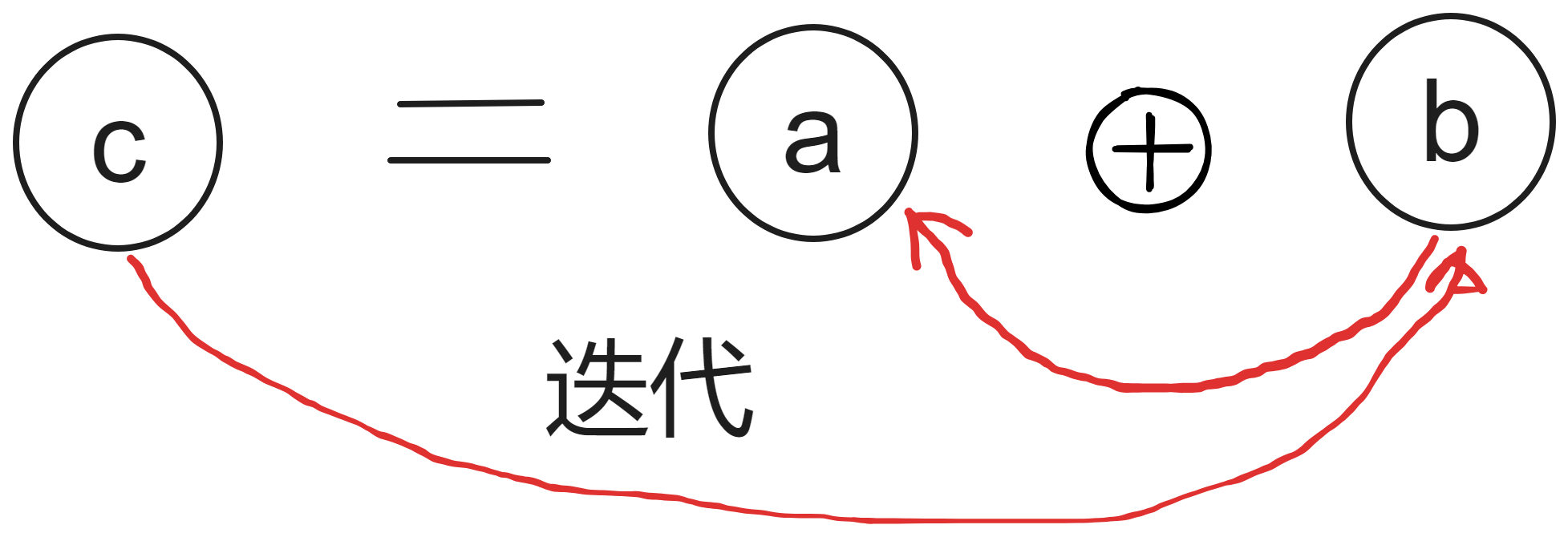
public class Fib04 {

    public int fib(int n) {
        int a = 1;
        int b = 1;
        int c = 0;
        for (int i = 3; i <= n; i++) {
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }

    public static void main(String[] args) {
        System.out.println(new Fib04().fib(5));
    }
}