2024年大湾区杯粤港澳金融数学建模B题超详细解题代码+数据集分享+问题一代码分享
2024 年(第五届)“大湾区杯”粤港澳金融数学建模竞赛B题超详细解题思路
B 题 粤港澳大湾区经济预测数学模型
本届大湾区杯11.1开赛,比赛时长天。为了尽可以的为大家提供帮助,我们将在11.2日早六点之前发布B题完整的论文、收集数据集、求解代码等资料,以便大家可以在后续的六天进行参考使用。本次竞赛我们将对B题提供相关的助攻。B题数据集需自行收集,这也意味着B题是不存在标准答案的,对于不同的数据集即使使用相同的模型也会得到完全不同的结果。因此,我们只需要把控合适的模型并进行精细的论文排版、可视化基本上就可以获得一个较为满意的结果。
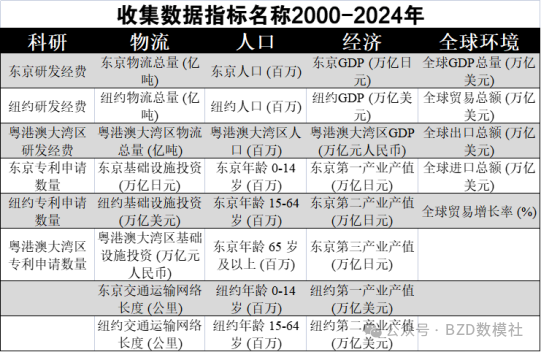
对于该题目首先就是数据的收集,为了让给大家提供多种数据选择方案,我们基于题目的要求为大家收集了GDP、人口数量、人口年龄结构、受教育情况、科技投入数据(研发经费、专利数等)、物流和基础设施数据(交通运输情况等)国际环境数据(全球经济形势、国际贸易环境)等数据集。以便大家可以根据自己解题需要,自行选择数据。
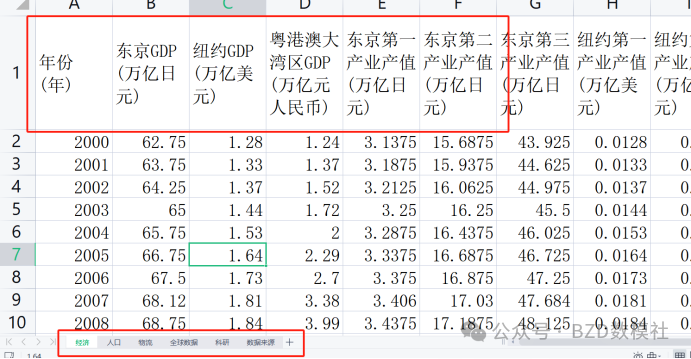
对于收集到的数据,首先需要进行必要的数据预处理,我们的数据基本来自于统计年鉴、各种网站。其来源不一定具有真实性,需要对数据进一步处理。主要包括,缺失值处理、时间处理、异常值处理、数据描述性分析。
1、缺失值处理;对于题目存在的大量缺失值,我们可以选择插值填充。【即使,在我给出的数据集中已经做好了插值工作,并无缺失值。这里我们也需要装模做样说存在缺失值。以便我们可以有更多的偏于进行可视化、文字描述,进行炫技】
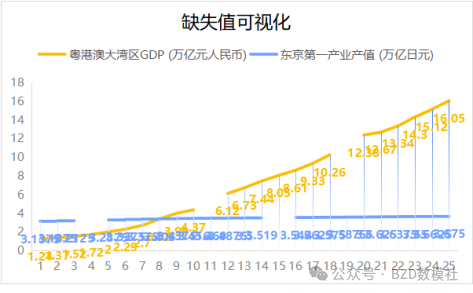
2、异常值处理,对于一直以来飞速发展的经济,24年间存在数据波动,有一定的异常值。即使该数据为真实数据,也需要对2008-2009年金融危机和2020-2021年新冠疫情进行必要的说明。
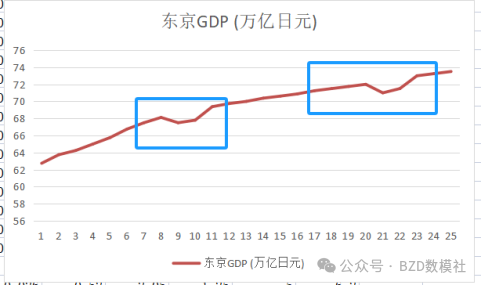
2、数据描述性分析;我们可以对收集的数据进行必要的可视化,进一步进行描述分析
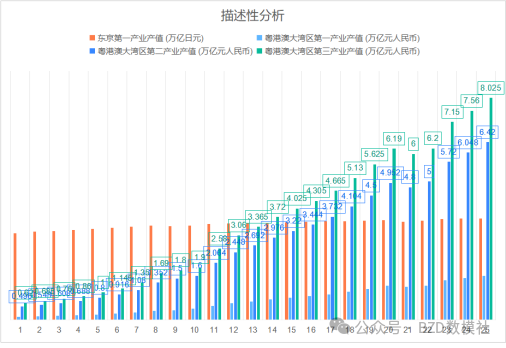
任务一:影响区域经济发展的因素分析与量化评价
1、数据收集与准备收集粤港澳大湾区的历史数据,包括GDP、人口、科技投入、产业结构、物流数据等
将这些数据进行分类,可以得到以下主要的类别:
·科研:例如东京研发经费、纽约研发经费、粤港澳大湾区研发经费等。
·物流:包括物流总量、交通运输网络长度、基础设施投资等。
·人口:各区域人口的年龄结构(0-14岁、15-64岁、65岁及以上)。
·经济:GDP、产业产值(第一、第二、第三产业)等。
·全球环境:全球进出口总额、全球贸易增长率等。
2、因素的量化评价
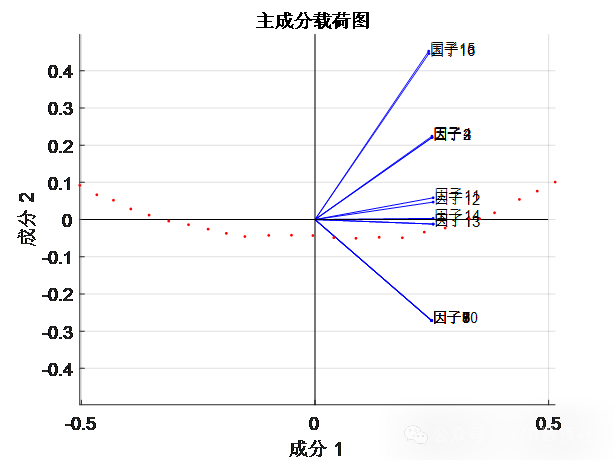
主成分分析 (PCA) 或 因子分析:
这些方法可以用于减少变量的维数,提取出影响经济发展的主要成分。
对数据进行标准化处理后,通过主成分分析,找出科研、物流、人口、经济等因素中最能解释区域经济波动的几个关键因素。
多元线性回归分析:
建立多元线性回归模型,以粤港澳大湾区的经济指标(如GDP或产业产值)作为因变量,以科研、物流、人口等指标作为自变量。
通过回归模型,可以得到每个因素对经济发展的影响系数,从而量化各因素的重要性。
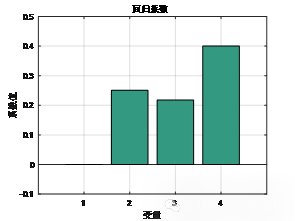
估计系数:
Estimate SE tStat pValue
___________ __________ ___________ __________
(Intercept) -1.5276e-16 0.0028852 -5.2945e-14 1
x1 0.25056 0.00074502 336.32 1.1389e-40
x2 0.21789 0.0049339 44.162 3.3597e-22
x3 0.40063 0.025701 15.588 5.1111e-13
观测值数目: 25,误差自由度: 21
均方根误差: 0.0144
R 方: 1,调整 R 方 1
F 统计量(常量模型): 3.84e+04,p 值 = 2.05e-39
3. 因素分级与排序
根据回归分析的结果,按对GDP的贡献度对各因素进行分级。可以把因素分为以下三类:
核心因素:对经济发展贡献度最大的因素,如某一特定的科研投入或者物流效率。
次要因素:有较明显影响但不及核心因素的,如某些基础设施投资。
辅助因素:影响较小的因素,如特定年龄段人口增长的变化等。
任务二:经济预测模型建立与策略制定
1. 经济预测模型的选择
时间序列模型:使用ARIMA模型来分析经济指标(如GDP、产业产值)随时间的变化情况,并预测未来5-10年的走势。
机器学习模型:
使用随机森林回归或XGBoost等算法,结合科研、物流、人口等多维度的特征,建立经济预测模型。
利用收集的历史数据进行训练,找出重要特征,预测未来的经济走势。
2. 模型构建与验证
利用2000年至2024年之间的数据,分为训练集和验证集。用2000-2018年的数据进行训练,用2019-2024年的数据进行验证。
通过多次迭代和调整参数,验证模型的预测精度,选择表现最优的模型进行最终预测。
3. 经济走势预测
通过模型预测未来5-10年的粤港澳大湾区GDP及产业结构的变化情况。
建立不同情景假设(如高研发投入、物流效率提升等),分析在不同条件下经济可能的走势。
任务三:其他湾区的对比分析
1. 选择比较的湾区
在提供的数据中,已经收集了东京和纽约的相关数据,可以对它们进行分析,作为对比对象。
采用与粤港澳大湾区相同的分析方法,对东京和纽约湾区的数据进行因素分析和经济预测。
2. 同样的模型与分析方法
利用相同的主成分分析、多元线性回归以及时间序列模型,对东京和纽约湾区进行建模,找出影响其经济的关键因素并预测未来5-10年的经济走势。
3. 量化分析不同湾区的发展异同
将三大湾区的预测结果进行对比,分析其发展的异同。
异同点分析:
不同的核心因素:比如,东京湾区可能科研投入是主要影响因素,而粤港澳大湾区则可能是物流和基础设施。
相同的影响因素:比如,人口结构中15-64岁劳动人口占比对各湾区经济均有显著影响。
定量对比不同湾区的科研投入、物流效率、基础设施建设对经济的影响,并分析各自优势与短板。
任务四:简报撰写
非技术型文章,这里就需要大家八仙过海各显神通了,基于上述的结果进行写出一篇简单的非技术型文章即可。
data = xlsread('问题一数据集.xlsx');
% 分割数据
X = data(:, 1:end-1); % 影响因素数据
Y = data(:, end); % GDP数据
% 2. 数据标准化
X_norm = zscore(X);
Y_norm = zscore(Y);
% 3. 主成分分析 (PCA)
[coeff, score, latent, tsquared, explained] = pca(X_norm);
% 可视化主成分贡献率
figure;
pareto(explained);
title('主成分贡献率', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('主成分', 'FontSize', 12);
ylabel('贡献率 (%)', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
% 可视化主成分载荷图(前两个主成分)
% 修改标签以确保它们与输入数据的特征数一致
num_vars = size(X, 2);
var_labels = strcat('因子', string(1:num_vars));
figure;
biplot(coeff(:, 1:2), 'Scores', score(:, 1:2), 'Varlabels', var_labels);
title('主成分载荷图', 'FontSize', 14, 'FontWeight', 'bold');
grid on;
set(gca, 'FontSize', 12);
% 4. 选择前几个主要成分
% 根据贡献率选择前k个成分,假设我们选择前3个成分
k = 3;
X_pca = score(:, 1:k);
% 5. 多元线性回归模型建立
mdl = fitlm(X_pca, Y_norm);
disp(mdl);
% 6. 回归系数可视化
figure;
bar(mdl.Coefficients.Estimate, 'FaceColor', [0.2 0.6 0.5]);
title('回归系数', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('变量', 'FontSize', 12);
ylabel('系数值', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
xlim([0 length(mdl.Coefficients.Estimate) + 1]);
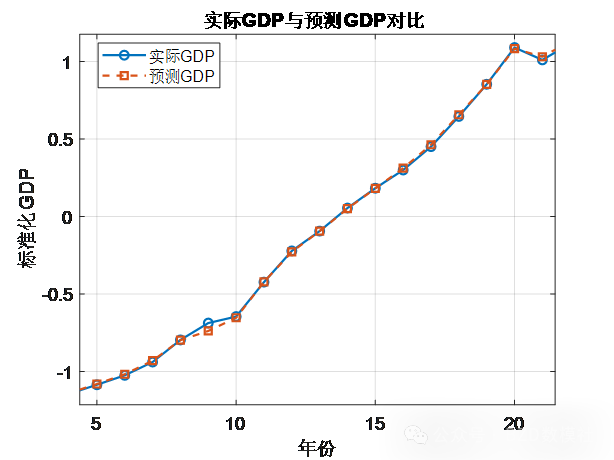
% 7. GDP 预测和结果可视化
Y_pred = predict(mdl, X_pca);
% 可视化实际GDP与预测GDP对比
figure;
plot(1:length(Y_norm), Y_norm, '-o', 'Color', [0 0.4470 0.7410], 'LineWidth', 1.5, 'MarkerSize', 6);
hold on;
plot(1:length(Y_pred), Y_pred, '--s', 'Color', [0.8500 0.3250 0.0980], 'LineWidth', 1.5, 'MarkerSize', 6);
legend('实际GDP', '预测GDP', 'Location', 'Best');
title('实际GDP与预测GDP对比', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('年份', 'FontSize', 12);
ylabel('标准化GDP', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
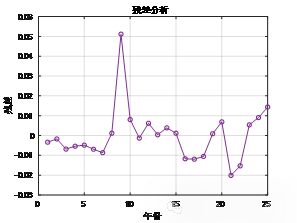
% 8. 残差分析
figure;
residuals = Y_norm - Y_pred;
plot(1:length(residuals), residuals, '-o', 'Color', [0.4940 0.1840 0.5560], 'LineWidth', 1.5, 'MarkerSize', 6);
title('残差分析', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('年份', 'FontSize', 12);
ylabel('残差', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
% 残差直方图可视化
figure;
histogram(residuals, 'FaceColor', [0.4660 0.6740 0.1880]);
title('残差直方图', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('残差值', 'FontSize', 12);
ylabel('频数', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
