【蓝桥杯专题】 树状数组(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ
文章目录
- 【蓝桥杯专题】 (C++ | 洛谷 | acwing | 蓝桥)
- 什么是线段数组??
- 1264. 动态求连续区间和
- 数星星
- 线段树
- AcWing 1270. 数列区间最大值
- P
- P
- P
- P
- P
- P
- P

【蓝桥杯专题】 (C++ | 洛谷 | acwing | 蓝桥)
什么是线段数组??
OI wiki
- 树状数组是一种支持 单点修改 和 区间查询 的,代码量小的数据结构。
- 俩个操作的时间复杂度均为
O(logn)

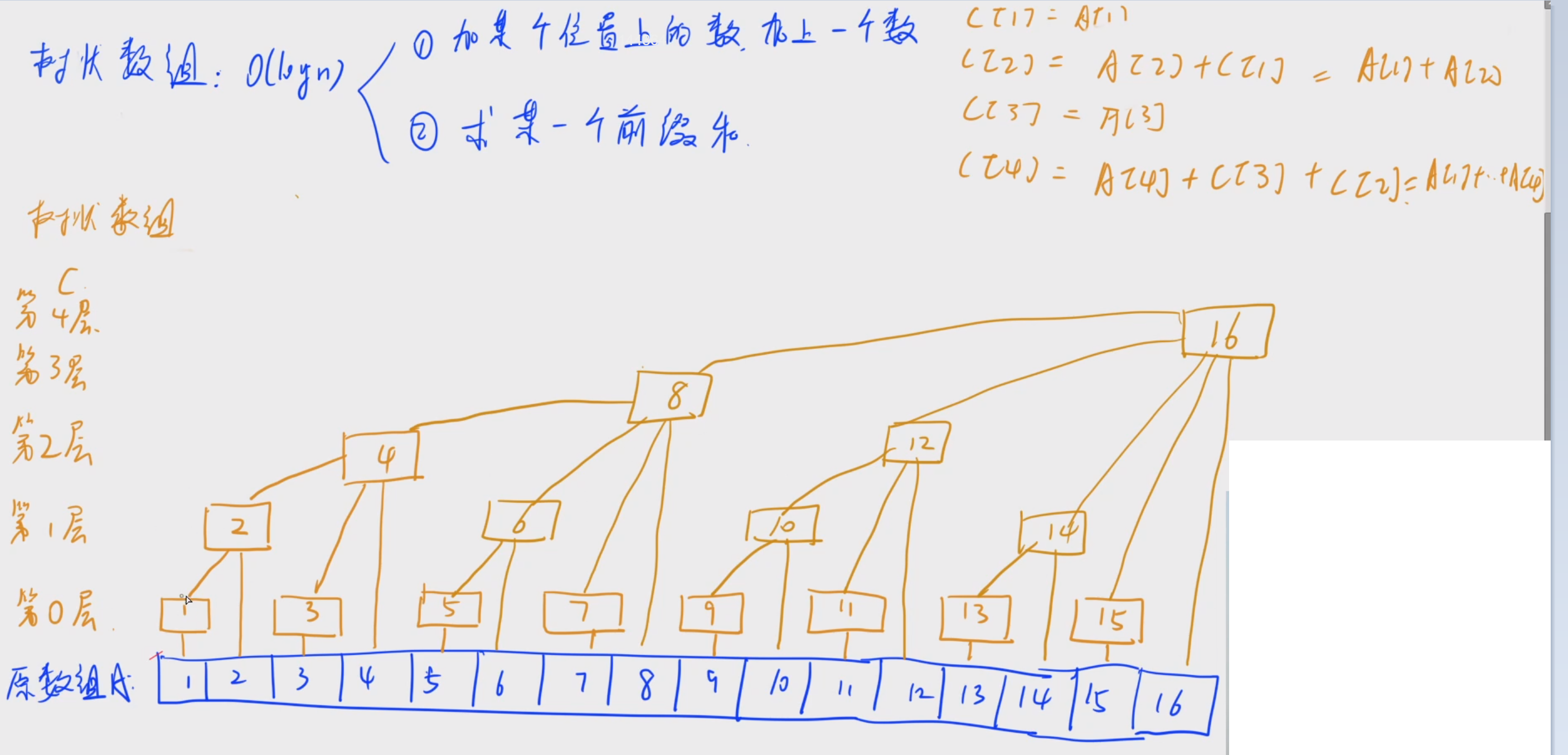
- lowbit()函数
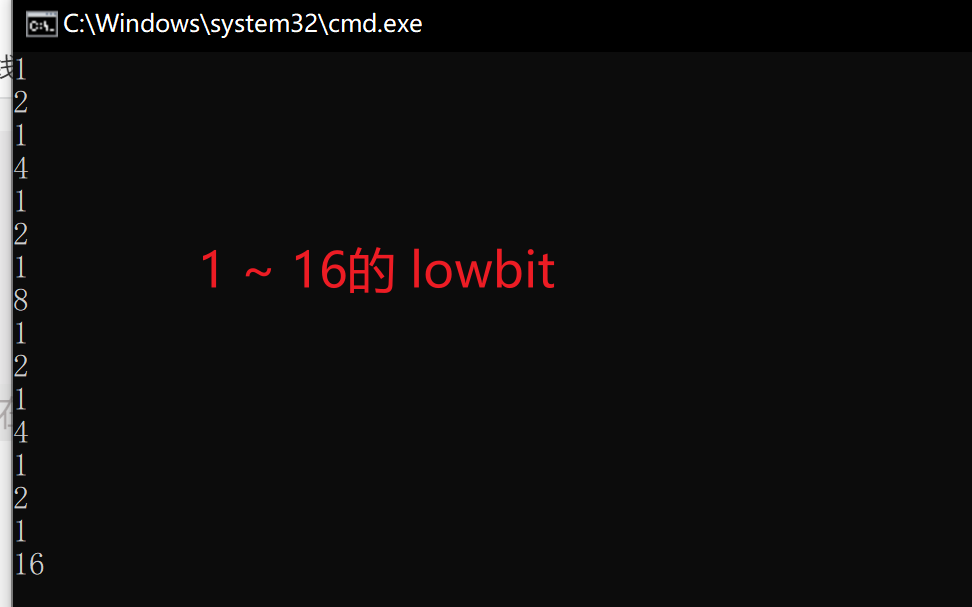
int lowbit(int x) { // 返回二进制中最后一个 1
// x 的二进制中,最低位的 1 以及后面所有 0 组成的数。
// lowbit(0b01011000) == 0b00001000
// ~~~~^~~~
// lowbit(0b01110010) == 0b00000010
// ~~~~~~^~
return x & -x;
}

1264. 动态求连续区间和

链接 链接
#include<bits/stdc++.h>
using namespace std;
const int N=100009;
int a[N],tr[N];
int n,m;
//每个数的间隔,背下来就行
int lowbit(int x)
{
return x&-x;
}
//第x个数加上v
int add(int x,int v)
{
//因为树状数组的性质,加一个数,只影响logn个数,所有不用全加完
//从当前位置开始加,每个间隔是lowbit(i),一直加到最后
for(int i=x;i<=n;i+=lowbit(i))
tr[i]+=v;
}
//返回x的前缀和
int qurry(int x)
{
//因为树状数组的性质,求前缀和,只用加logn个数,所有不用全加完
//从当前位置开始累加,每个间隔是lowbit(i),一直加到i==0停止
int cnt=0;
for(int i=x;i!=0;i-=lowbit(i))
cnt+=tr[i];
return cnt;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
add(i,a[i]);//第i个数加上a[i]
while(m--)
{
int k,x,y;
scanf("%d%d%d",&k,&x,&y);
if(k==0) printf("%d\n",qurry(y)-qurry(x-1));
else add(x,y);
}
return 0;
}
数星星
由于本题输入数据很特殊,所以其实等价于求一下,到目前的输入为止,有多少个星星的 x 值小于等于该星星的 x 就可以了,这就代表该星星的等级。
由于该题y不递减的输入特性,导致了y在题目中毫无作用
链接 链接
#include <bits/stdc++.h>
// #include <iostream>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define per(i, a, n) for(int i = n; i <= a; i --)
#define pb push_back;
#define fs first;
#define sz second;
#include <stdlib.h> // atoi
#define debug cout<<"debug"<<"\n"
#define endl "\n";
const int INF = 0x3f3f3f3f;
const int mod=1e9+7;
const int N = 1e5 + 10;
int n;
int ans[N];
int c[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int v) {
//更新整棵树
for(int i = x; i <= 32001; i += lowbit(i)) {
c[i] += v;
}
}
// 计算前缀和
int query(int x) {
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) res += c[i];
return res;
}
void solve () {
cin >> n;
rep(i, 1, n) {
int x, y;
cin >> x >> y;
x ++;/*为了防止出现0的情况,给它全体横坐标加上 1 就好了。
这其实是一个很小的细节,作者但是做的时候没考虑到然后就wa了,而给每个 x 都加上 1 并不会影响结果*/
add(x, 1);
ans[query(x)] ++;
/*然后查一下它的前缀和是多少,前缀和是多少就意味着是多少级
这是一个动态变化的过程,而且后面的一定比前面高
所以要实时计算*/
}
for(int i = 1;i <= n; i ++) {
printf("%d\n",ans[i]);//输出每一个等级的数量
}
}
int main(void){
freopen("in.txt","r",stdin);
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int T = 1;
// cin >> T;
while(T --) solve();
return 0;
}
线段树
链接 链接
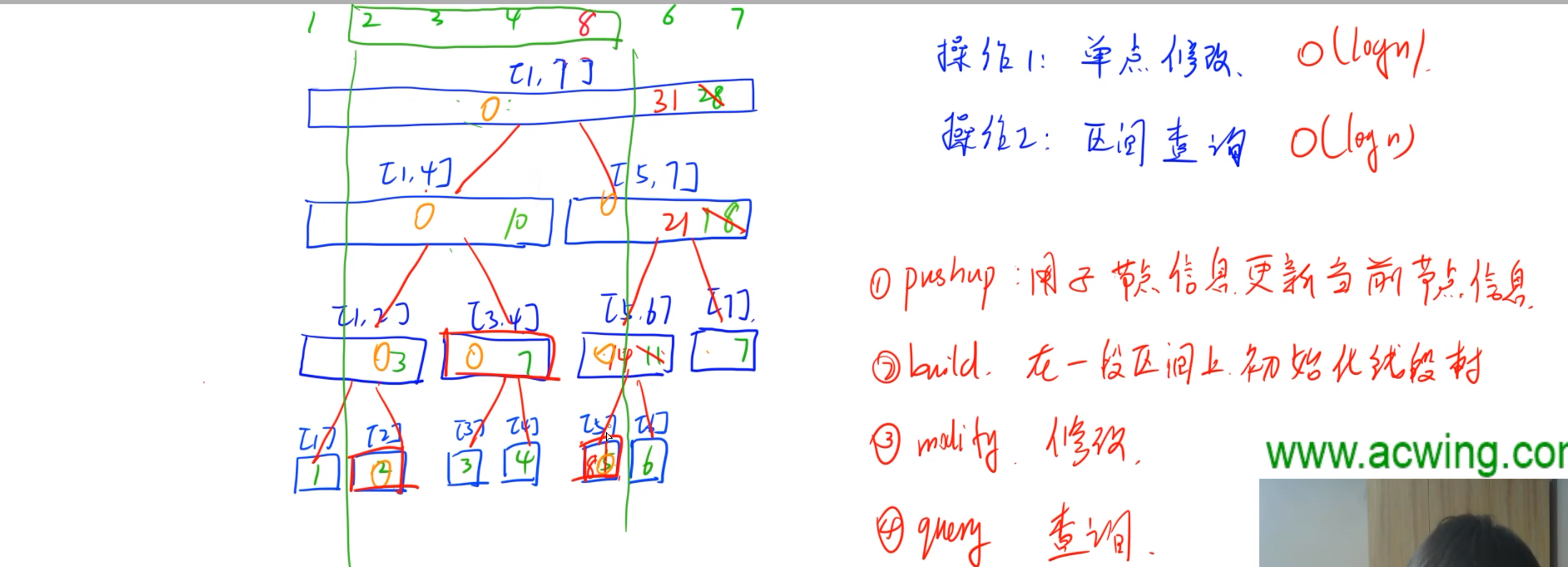
支持:单点修改 区间查询 , 时间复杂度均为log n
//定义节点
struct node{
int l,r;//左右区间
int sum;//总和
}tr[N*4];//记得开 4 倍空间 (满2叉树 2N - 1 还有空节点 所以为 4N)
void push_up(int u) {//利用它的两个儿子来算一下它的当前节点信息
//左儿子 u<<1 ,右儿子 u<<1|1
}
void build(int u,int l,int r) {/*第一个参数,当前节点编号,第二个参数,左边界,第三个参数,右边界*/
//如果当前已经是叶节点了,那我们就直接赋值就可以了
//否则的话,说明当前区间长度至少是 2 对吧,那么我们需要把当前区间分为左右两个区间,那先要找边界点
//这里记得赋值一下左右边界的初值
//边界的话直接去计算一下 l + r 的下取整
//先递归一下左儿子
//然后递归一下右儿子
//做完两个儿子之后的话呢 push_up 一遍u 啊,更新一下当前节点信息
}
int query(int u,int l,int r)//查询的过程是从根结点开始往下找对应的一个区间
{
//如果当前区间已经完全被包含了,那么我们直接返回它的值就可以了
//否则的话我们需要去递归来算
//计算一下我们 当前 区间的中点是多少
//先判断一下和左边有没有交集
//用 sum 来表示一下我们的总和
//看一下我们当前区间的中点和左边有没有交集
//看一下我们当前区间的中点和右边有没有交集
}
void modify(int u,int x,int v)//第一个参数也就是当前节点的编号,第二个参数是要修改的位置,第三个参数是要修改的值
{
//如果当前已经是叶节点了,那我们就直接让他的总和加上 v 就可以了
//否则
//看一下 x 是在左半边还是在右半边
//如果在右半边,那就找右儿子
//更新完之后当前节点的信息就要发生变化对吧,那么我们就需要 pushup 一遍
}
AcWing 1270. 数列区间最大值
链接 链接
- 思路和线段树类似, sum 改为 maxv
#include <iostream>
#include <cstring>
#include <algorithm>
#include <limits.h>
using namespace std;
const int N = 100010;
int w[N], n, m;
struct Segnode {
int l, r, maxv; // 把记录区间和的sum换成了记录区间最大值的maxv
}seg[4 * N];
void build (int u, int l, int r) {
if(l == r) seg[u] = {l, r, w[r]};
else {
int mid = l + r >> 1;
seg[u] = {l , r};
build(u * 2, l, mid), build(u * 2 + 1, mid +1 , r);
seg[u].maxv = max (seg[u * 2].maxv, seg[u * 2 + 1].maxv);
}
}
int query(int u, int l, int r) {
if(seg[u].l >= l && seg[u].r <= r) return seg[u].maxv ;
int res = INT_MIN;
int mid = seg[u].l + seg[u].r >> 1;
if(r > mid ) res = max(res, query(u * 2 + 1, l , r));
if(l <= mid) res = max(res, query(u * 2 , l, r));
return res;
}
int main()
{
int l, r;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++ i) scanf("%d", &w[i]);
build(1, 1, n);
while (m --) {
scanf("%d %d", &l, &r);
printf("%d\n", query(1, l, r));
}
return 0;
}
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接

