贝叶斯+PINN！双重热点buff叠加，轻松斩获Nature子刊！

PINN一直以来都是顶会顶刊上的大热方向，相关研究量多且质量高。最近，有关“贝叶斯+PINN”的研究取得了不少突破，多项成果被Neurips、Nature子刊等录用。

事实上，这个结合方向的研究热度正逐渐上升，因为其在提高泛化能力、避免过拟合、增强可解释性、提高计算效率、鲁棒性强以及灵活性高等多方面都展现出了显著优势。这些优势也让“贝叶斯+PINN”适用于多种任务，在金融、医疗诊断与预测等多个领域都有非常广泛的应用。

因此，这种学术界和工业界公认的热点拥有很高的研究价值，对于我们论文er来说，也是个还没卷生卷死，创新空间依然很大的方向，感兴趣的同学可以抓紧上车。

如果需要参考，我这边也提供8篇贝叶斯+PINN相关的代表论文，有新的也有比较经典的，开源代码也都整理上了，需要的速领。

论文原文+开源代码需要的同学看文末

Bayesian Physics-Informed Extreme Learning Machine for Forward and Inverse PDE Problems with Noisy Data

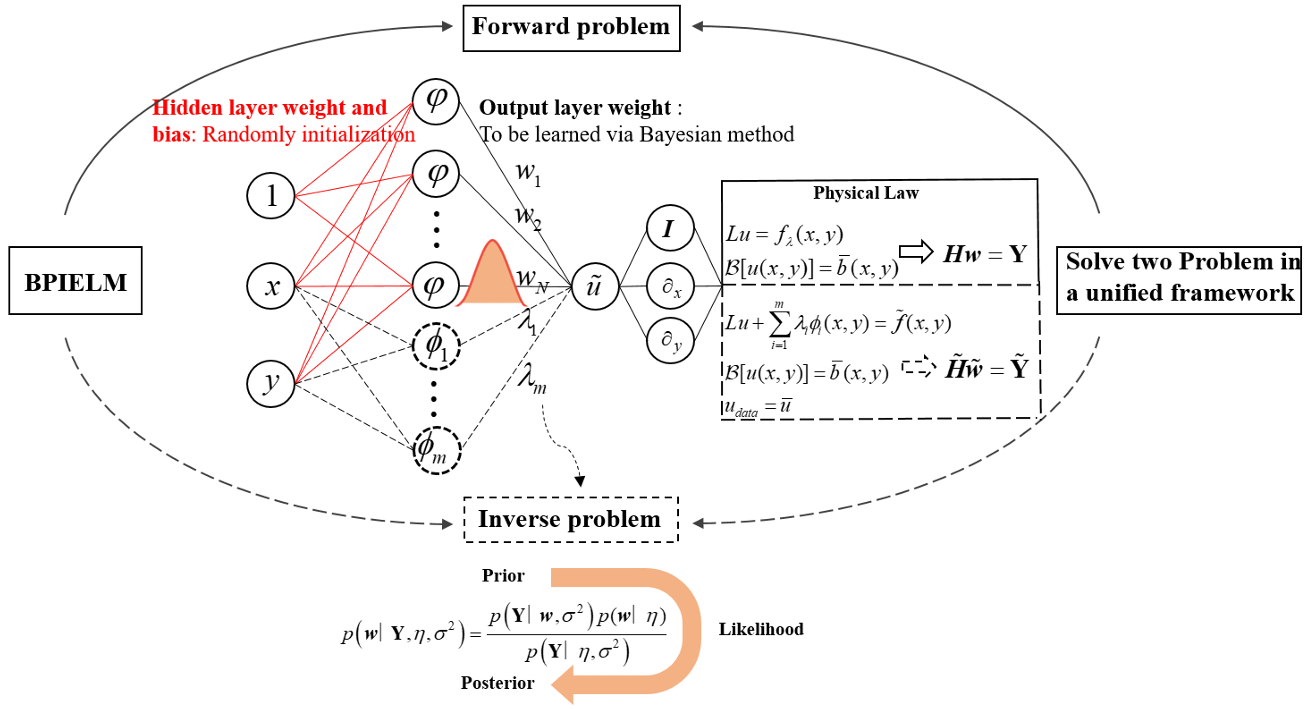
方法：本文提出了一种新的贝叶斯物理信息极限学习机（BPIELM），通过将物理定律作为成本函数引入极限学习机中，并结合贝叶斯方法来量化散乱噪声数据的不确定性，实验证明BPIELM在噪声场景下提供了更准确的预测和更低的计算成本，同时避免了过拟合问题。

创新点：

• BPIELM方法集成了物理信息神经网络（PINN）和物理信息极限学习机（PIELM）的优势，提供了一种在具有噪声的数据环境下解决偏微分方程（PDE）问题的创新方法。

• BPIELM通过贝叶斯方法来估计参数的后验分布，并量化预测的不确定性。

• BPIELM能够在一个统一的框架下有效解决逆问题，这在处理噪声场景下表现出竞争力。

Bayesian Physics-informed Neural Networks for System Identification of Inverter-dominated Power Systems

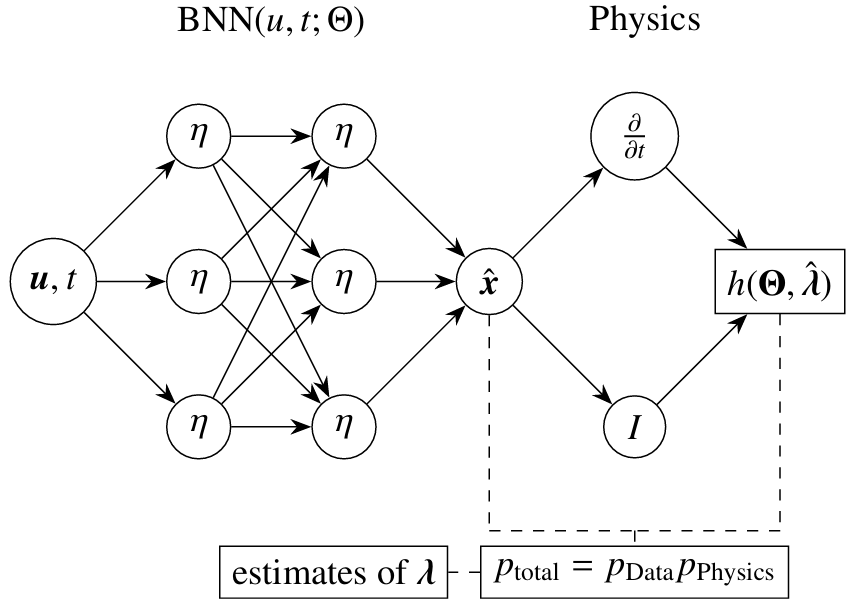
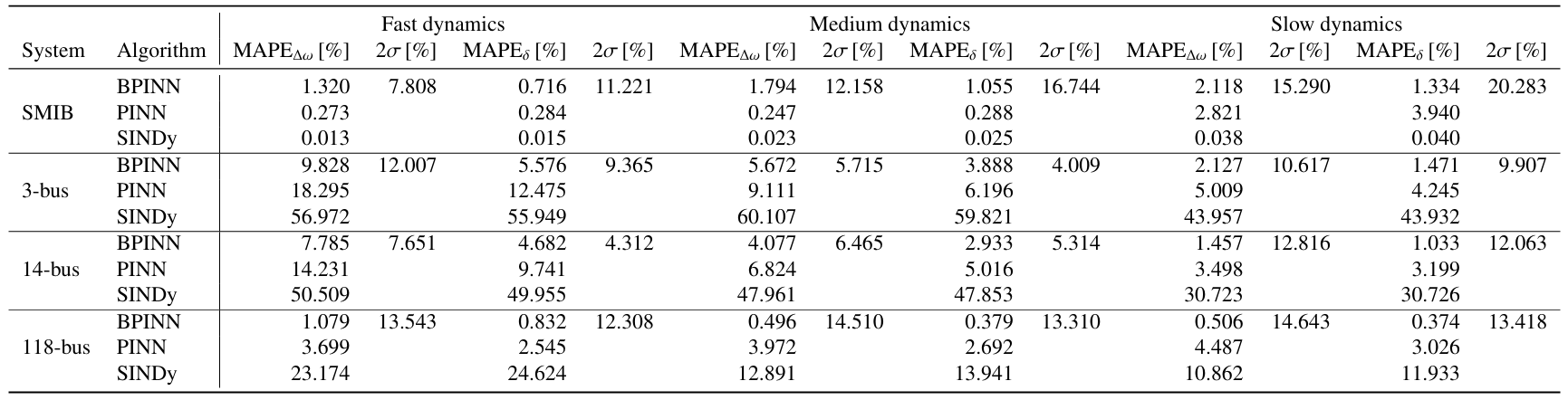
方法：作者引入了贝叶斯物理信息神经网络（BPINNs），结合PINNs的物理约束和贝叶斯方法的非确定性量化能力。结果表明，BPINN在不确定性条件下的误差远低于传统系统识别方法SINDy，并显著低于PINN。

创新点：

• 通过结合物理信息神经网络（PINN）和贝叶斯方法，BPINN在模型不确定性下能够提供更丰富的信息，如后验标准差，这在SINDy或传统的PINN中是无法获得的。

• 器主导的电力系统中频繁变动的系统参数，引入了弱信息先验。

• 通过迁移学习，BPINN显著减少了训练迭代次数和数据需求。在单机无限母线（SMIB）系统上的预训练能够有效转移到更大的118节点系统上，训练时间减少多达80%。

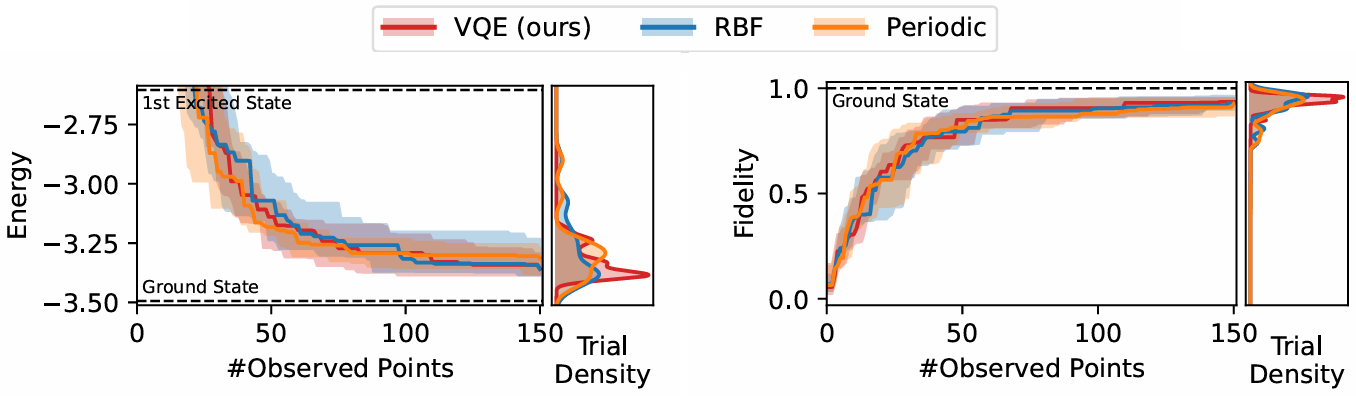
Physics-Informed Bayesian Optimization of Variational Quantum Circuits

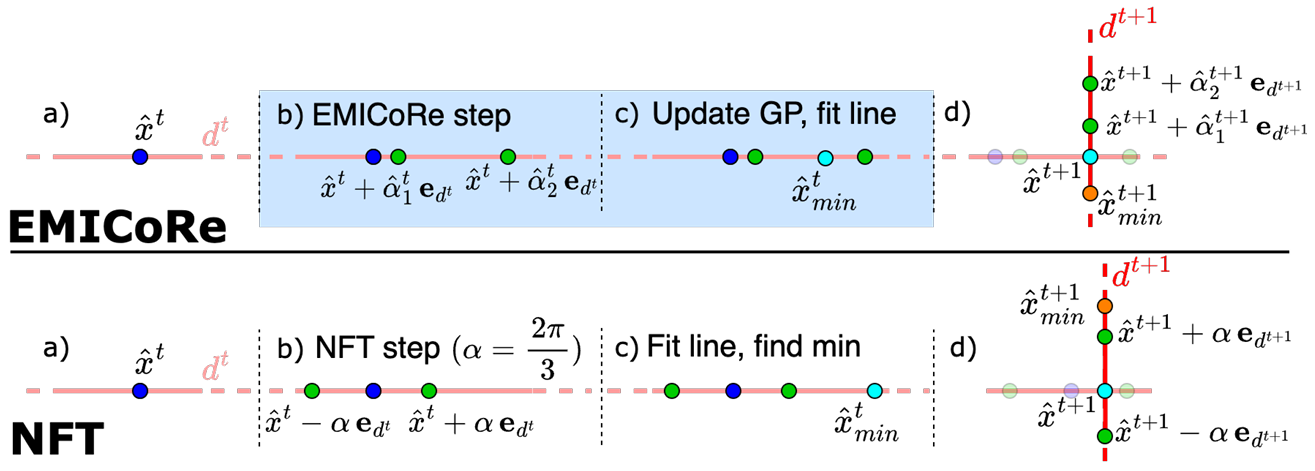
方法：本文提出了一种新颖的方法，将贝叶斯优化应用于变分量子特征求解器（VQE）中，通过引入包含物理先验信息的VQE核和一个名为EMICoRe的新获取函数，以提升优化效率、稳定性和抗噪性。

创新点：

• 提出了一种新的 VQE 核函数，该核函数通过与 VQE 目标函数的基础函数严格对齐，从而将强大的物理启发偏置融入到高斯过程（GP）回归中。

• 开发了一种新的采集函数，即“自信区域的期望最大改进”（EMICoRe）。该函数通过预测后验方差并将低方差点视为“已观测”点来运作。

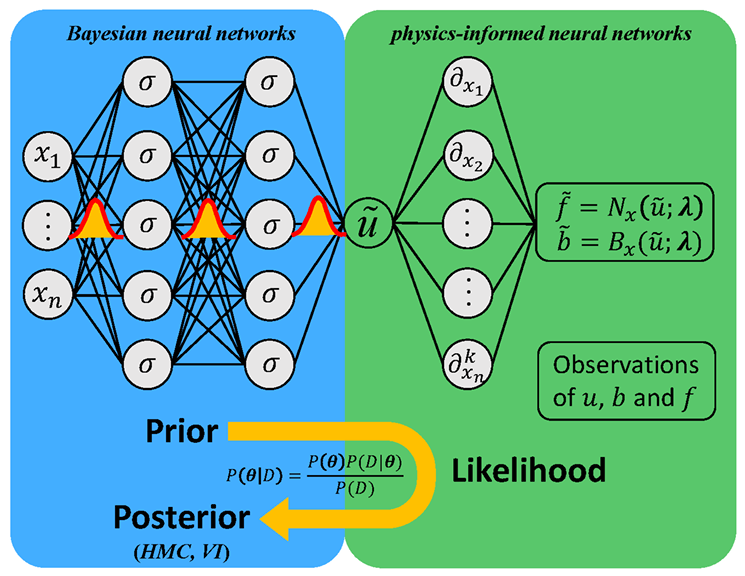
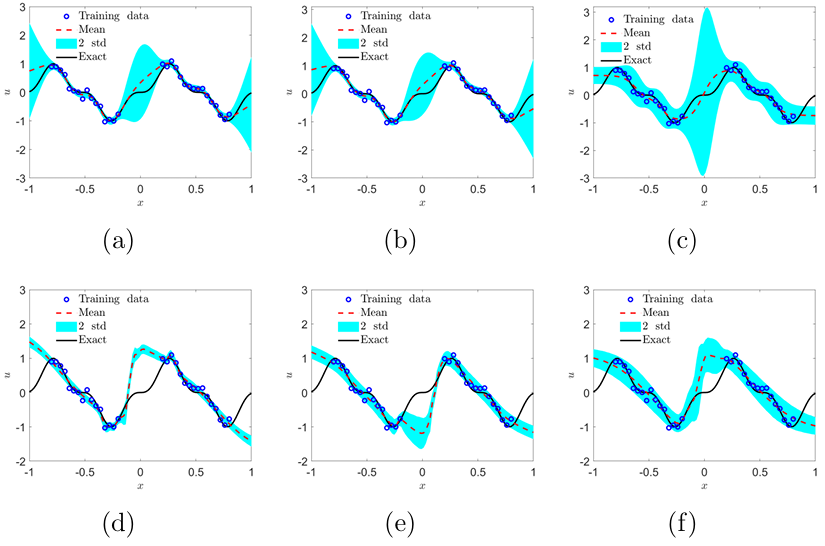
B-PINNs: Bayesian Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Noisy Data

方法：论文研究了贝叶斯物理信息神经网络（B-PINNs）在解决带噪声数据的偏微分方程问题中的应用，通过引入Hamiltonian Monte Carlo和变分推断（VI）等后验采样方法以及非贝叶斯框架的dropout，对比其在小数据集下的性能表现。

创新点：

• 提出了一种结合贝叶斯神经网络与PINN的新框架，将贝叶斯神经网络用于不确定性量化，并利用物理定律作为先验，提高了在有噪声数据情况下的预测准确性。

• 应用了两种后验分布采样方法，即哈密顿蒙特卡洛（HMC）和变分推断（VI），以提高对 PDE 问题的解决能力。

• 用KL展开替换BNN，提供了处理高维问题的另一种可能。

关注下方《学姐带你玩AI》🚀🚀🚀

回复“贝叶斯pinn”获取全部论文+开源代码

码字不易，欢迎大家点赞评论收藏