[双指针] 盛最多水的容器, 有效三角形的个数, 和为s的两个数
目录
一. 11. 盛最多水的容器 - 力扣(LeetCode)
二. 611. 有效三角形的个数 - 力扣(LeetCode)
三. LCR 179. 查找总价格为目标值的两个商品 - 力扣(LeetCode)
一. 11. 盛最多水的容器 - 力扣(LeetCode)
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
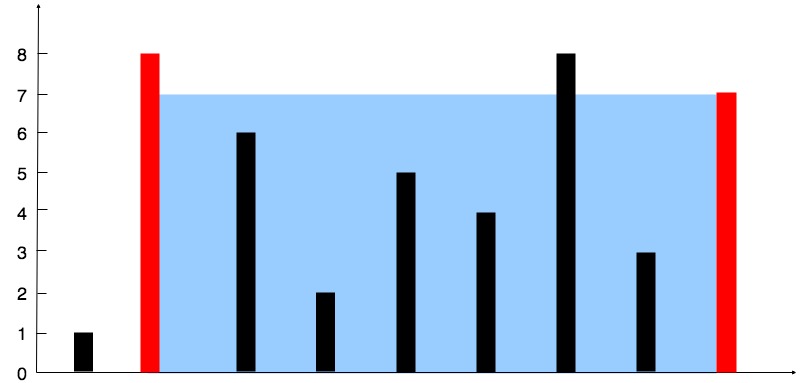
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
public int maxArea(int[] height) {
// 容积 = 短板长度 * 长短板之间的距离
// 双指针: 长短板之间距离减小, 那么短板长度需要增大, 容积才会增大 否则, 容积一定减小
int left = 0;
int right = height.length - 1;
int maxVal = 0; // 记录最大容积
while (left < right) {
int tmpVal = Math.min(height[left], height[right]) * (right - left);
if (tmpVal > maxVal) {
maxVal = tmpVal;
}
if (height[left] > height[right]) {
right--;
} else {
left++;
}
}
return maxVal;
}二. 611. 有效三角形的个数 - 力扣(LeetCode)
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3
示例 2:
输入: nums = [4,2,3,4] 输出: 4
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
public int triangleNumber(int[] nums) {
// 有效三角形: 两短边之和 > 第三长边
Arrays.sort(nums); // 升序数组
// 双指针
int n = nums.length - 1; // 长边
int left = 0;
int right = n - 1; // 两短边
int ret = 0;
while (n >= 2) {
left = 0;
right = n - 1;
while (left < right) {
if (nums[left] + nums[right] > nums[n]) {
ret += right - left;
right--;
} else {
left++;
}
}
n--;
}
return ret;
}三. 11. 盛最多水的容器 - 力扣(LeetCode)
购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。
示例 1:
输入:price = [3, 9, 12, 15], target = 18 输出:[3,15] 或者 [15,3]
示例 2:
输入:price = [8, 21, 27, 34, 52, 66], target = 61 输出:[27,34] 或者 [34,27]
public int[] twoSum(int[] price, int target) {
// 双指针(有序数组)
// left + right = target
int left = 0;
int right = price.length - 1;
while (left < right) {
if (price[left] > target - price[right]) {
right--;
} else if (price[left] < target - price[right]) {
left++;
} else {
int[] ret = {price[left], price[right]};
return ret;
}
}
return null;
}